AP SSC 10th Class Maths Solutions Chapter 6 Progressions Ex 6.4

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 6 Progressions Ex 6.4 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 6th Lesson Progressions Exercise 6.4

10th Class Maths 6th Lesson Progressions Ex 6.4 Textbook Questions and Answers

Question 1.
In which of the following situations, does the list of numbers involved in the form a G.P.?
i) Salary of Sharmila, when her salary is Rs. 5,00,000 for the first year and expected to receive yearly increase of 10% .
Answer:
Given: Sharmila’s yearly salary = Rs. 5,00,000.
Rate of annual increment = 10 %.

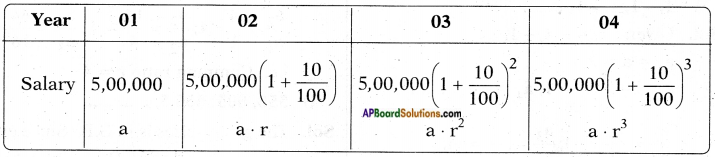
Here, a = a₁ = 5,00,000
a₂ = 5,00,000 × \(\frac{11}{10}\) = 5,50,000
a₃ = 5,00,000 × \(\frac{11}{10}\) × \(\frac{11}{10}\) = 6,05,000
a₄ = 5,00,000 × \(\frac{11}{10}\) × \(\frac{11}{10}\) × \(\frac{11}{10}\) = 6,65,000

Every term starting from the second can be obtained by multiplying its pre¬ceding term by a fixed number \(\frac{11}{10}\).
∴ r = common ratio = \(\frac{11}{10}\)
Hence the situation forms a G.P.

ii) Number of bricks needed to make each step, if the stair case has total 30 steps. Bottom step needs 100 bricks and each successive step needs 2 bricks less than the previous step.
Answer:
Given: Bricks needed for the bottom step = 100.
Each successive step needs 2 bricks less than the previous step.
∴ Second step from the bottom needs = 100 – 2 = 98 bricks.
Third step from the bottom needs = 98 – 2 = 96 bricks.
Fourth step from the bottom needs = 96 – 2 = 94 bricks.
Here the numbers are 100, 98, 96, 94, ….
Clearly this is an A.P. but not G.P.

iii) Perimeter of the each triangle, when the mid-points of sides of an equilateral triangle whose side is 24 cm are joined to form another triangle, whose mid-points in turn are joined to form still another triangle and the process continues indefinitely.

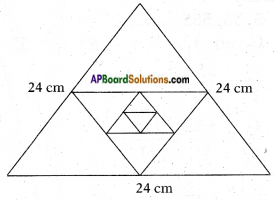
Answer:
Given: An equilateral triangle whose perimeter = 24 cm.
Side of the equilateral triangle = \(\frac{24}{3}\) = 8 cm.
[∵ All sides of equilateral are equal] ……. (1)
Now each side of the triangle formed by joining the mid-points of the above triangle in step (1) = \(\frac{8}{2}\) = 4 cm
[∵ A line joining the mid-points of any two sides of a triangle is equal to half the third side.]
Similarly, the side of third triangle = \(\frac{4}{2}\) = 2 cm
∴ The sides of the triangles so formed are 8 cm, 4 cm, 2 cm,
a = 8

Thus each term starting from the second; can be obtained by multiplying its preceding term by a fixed number \(\frac{1}{2}\).
∴ The situation forms a G.P.

Question 2.
Write three terms of the G.P. when the first term ‘a’ and the common ratio ‘r’ are given.
i) a = 4 ; r = 3.
Answer:
The terms are a, ar, ar², ar³, ……..
∴ 4, 4 × 3, 4 × 3² , 4 × 3² , ……
⇒ 4, 12, 36, 108, ……

ii) a = √5 ; r = \(\frac{1}{5}\)
Answer:
The terms are a, ar, ar², ar³, ……..

iii) a = 81 ; r = –\(\frac{1}{3}\)
Answer:
The terms of a G.P are:
a, ar, ar², ar³, ……..

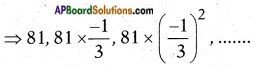
⇒ 81, -27, 9,

iv) a = \(\frac{1}{64}\); r = 2.
Answer:
Given: a = \(\frac{1}{64}\); r = 2.

∴ The G.P is \(\frac{1}{64}\), \(\frac{1}{32}\), \(\frac{1}{16}\), …….

Question 3.
Which of the following are G.P. ? If they are G.P, write three more terms,
i) 4, 8, 16, ……
Answer:
Given: 4, 8, 16, ……
where, a₁ = 4; a₂ = 8; a₃ = 16, ……
\(\frac{a_{2}}{a_{1}}=\frac{8}{4}=2\)
\(\frac{a_{3}}{a_{2}}=\frac{16}{8}=2\)
∴ r = \(\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}\) = 2
Hence 4, 8, 16, … is a G.P.
where a = 4 and r = 2
a₄ = a . r³ = 4 × 2³ = 4 × 8 = 32
a₅ = a . r⁴ = 4 × 2⁴ = 4 × 16 = 64
a₆ = a . r⁵ = 4 × 2⁵ = 4 × 32 = 128

ii) \(\frac{1}{3}\), –\(\frac{1}{6}\), \(\frac{1}{12}\), …….
Answer:
Given: t₁ = \(\frac{1}{3}\), t₂ = –\(\frac{1}{6}\), t₃ = \(\frac{1}{12}\), ….
\(\frac{1}{3}\), –\(\frac{1}{6}\), \(\frac{1}{12}\), …….

Hence the ratio is common between any two successive terms.
∴ \(\frac{1}{3}\), –\(\frac{1}{6}\), \(\frac{1}{12}\), ……. is G.P.
where a = \(\frac{1}{3}\) and r = –\(\frac{1}{2}\)

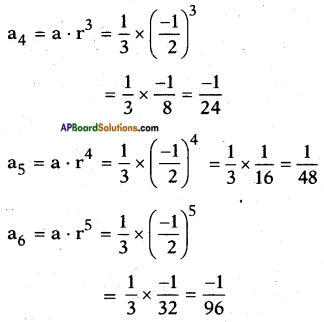
iii) 5, 55, 555, ……..
Answer:
Given: t₁ = 5, t₂ = 55, t₃ = 555, ….

∴ 5, 55, 555, …….. is not a G.P.

iv) -2, -6, -18, ……
Given: t₁ = -2, t₂ = -6, t₃ = -18

∴ -2, -6, -18, is a G.P.
where a = -2 and r = 3
a_n = a . r^n-1 =
a₄ = a . r³ = (-2) × 3³ = -2 × 27 = -54
a₅ = a . r⁴ = (-2) × 3⁴ = -2 × 81 = -162
a₆ = a . r⁵ = (-2) × 3⁵ = -2 × 243 = -486

v) \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), …….
Answer:

i.e., \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), ….. is not a G.P.

vi) 3, -3², 3³, ……
Given: t₁ = 3, t₂ = -3², t₃ = 3³, ……


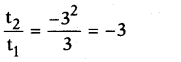
i.e., every term is obtained by multiplying its preceding term by a fixed number -3.
3, -3², 3³, …… forms a G.P,
where a = 3; r = -3
a_n = a . r^n-1
a₄ = a . r³ = 3 × (-3)³ = 3 × (-27) = -81
a₅ = a . r⁴ = 3 × (-3)⁴ = 3 × 81 = 243
a₆ = a . r⁵ = 3 × (-3)⁵ = 3 × (-243) = -729

vii) x, 1, \(\frac{1}{x}\), …….
Answer:
Given: t₁ = x, t₂ = 1, t₃ = \(\frac{1}{x}\), ……

Hence x, 1, \(\frac{1}{x}\), …. forms a G.P.
where a = x; r = \(\frac{1}{x}\)

viii) \(\frac{1}{\sqrt{2}}\), -2, \(\frac{8}{\sqrt{2}}\), …….
Answer:
Given: t₁ = \(\frac{1}{\sqrt{2}}\), t₂ = -2, t₃ = \(\frac{8}{\sqrt{2}}\), ……

ix) 0.4, 0.04, 0.004, ……..
Answer:
Given: t₁ = 0.4, t₂ = 0.04, t₃ = 0.004, ……

∴ 0.4, 0.04, 0.004, …….. forms a G.P.
where a = 0.4; r = \(\frac{1}{10}\)

Question 4.
Find x so that x, x + 2, x + 6 are consecutive terms of a geometric progression.
Answer:
Given x, x + 2 and x + 6 are in G.P. but read it as x, x + 2 and x + 6.
∴ r = \(\frac{\mathrm{t}_{2}}{\mathrm{t}_{1}}\) = \(\frac{\mathrm{t}_{3}}{\mathrm{t}_{2}}\)
⇒ \(\frac{x+2}{x}\) = \(\frac{x+6}{x+2}\)
⇒(x + 2)² = x(x + 6)
⇒ x² + 4x + 4 = x² + 6x
⇒ 4x – 6x = – 4 = -2x = -4
∴ x = 2