AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 5 Quadratic Equations Ex 5.1 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 5th Lesson Quadratic Equations Exercise 5.1
10th Class Maths 5th Lesson Quadratic Equations Ex 5.1 Textbook Questions and Answers
Question 1.
Check whether the following are quadratic equations.
i) (x + l)2 = 2(x-3)
Answer:
Given: (x + l)2 = 2(x – 3)
⇒ x2 + 2x + 1 = 2(x – 3) = 2x – 6
⇒ x2 + 2x + l – 2x + 6 = 0
⇒ x2 + 7 = 0 is a Q.E.
ii) x2 – 2x = (-2) (3 – x)
Answer:
Given: x2 – 2x = -2(3 – x)
⇒ x2 – 2x = -6 + 2x
⇒ x2 – 4x + 6 = 0 is a Q.E.
![]()
iii) (x-2) (x + 1) = (x- 1) (x + 3)
Answer:
Given: (x – 2) (x + 1) = (x – 1) (x + 3)
⇒ x (x + 1) – 2 (x +1)
= x (x + 3) – 1 (x + 3)
Note : Compare the coefficients of x2 on both sides. If they are equal it is not a Q.E.
⇒ x2 + x – 2x – 2 = x2 + 3x – x -3
⇒ x2 – x – 2 = x2 + 2x – 3
⇒ 3x – 1 = 0 is not a Q.E.
iv) (x – 3) (2x + 1) = x(x + 5)
Answer:
Given: (x – 3) (2x + 1) = x(x + 5)
⇒ x (2x + 1) – 3 (2x + 1) = x . x + 5 . x
⇒ 2x2 + x – 6x – 3 = x2 + 5x
⇒ 2x2 – 5x – 3 – x2 – 5x = 0
⇒ x2 – 10x – 3 = 0 is a Q.E.
(or)
Comparing the coefficients of x2 on both sides.
x . 2x and x . x
⇒ 2x2 and x2
2x2 ≠ x2
Hence it’s a Q.E.
v) (2x – 1) (x – 3) = (x + 5) (x – 1)
Answer:
Given: (2x – 1) (x – 3) = (x + 5) (x – 1)
⇒ 2x (x – 3) -1 (x – 3) = x (x – 1) + 5(x – 1)
⇒ 2x2 – 6x – x + 3 = x2 – x + 5x – 5
⇒ 2x2 -7x + 3 – x2 – 4x + 5 = 0
⇒ x2 – 11x + 8 = 0
Hence it’s a Q.E.
(or)
Co.eff. of x2 on L.H.S. = 2 × 1 = 2
Co.eff. of x2 on R.H.S = 1 × 1 = 1
LHS ≠ RHS Hence it is a Q.E.
vi) x2 + 3x + 1 = (x – 2)2
Answer:
Given: x2 + 3x + 1 = (x – 2)2
⇒ x2 + 3x + 1 = x2 – 4x + 4
⇒ 7x – 3 = 0 is not a Q.E.
![]()
vii) (x + 2)3 = 2x (x2 – 1)
Answer:
Given: (x + 2)3 = 2x(x2 – 1)
⇒ x3 + 6x2 + 12x + 8 = 2x3 – 2x [∵ (a + b)3 = a3 + 3a2b + 3ab2 + b3]
⇒ -x3 + 6x2 + 14x + 8 = 0
is not a Q.E. [∵ degree = 3]
viii) x3 – 4x2 – x + 1 = (x – 2)3
Answer:
Given : x3 – 4x2 – x + 1 = (x – 2)3
⇒ x3 – 4x2 – x + 1 = x3 – 6x2 + 12x – 8
⇒ 6x2 – 12x + 8 – 4x2 – x + 1 = 0
⇒ 2x2 – 13x + 9 = 0 is a Q.E.
Question 2.
Represent the following situations in the form of quadratic equations:
i) The area of a rectangular plot is 528 m2. The length of the plot (in meters) is one more than twice its breadth. We need to find the length and breadth of the plot.
Answer:
Let the breadth of the rectangular plot be x m.
Then its length (by problem) = 2x + 1.
Area = l . b = (2x + 1) . x = 2x2 + x
But area = 528 m2 (∵ given)
∴ 2x2 + x = 528
⇒ 2x2 + x – 528 = 0 where x is the breadth of the rectangle.
ii) The product of two consecutive positive integers is 306. We need to find the integers.
Answer:
Let the consecutive integers be x and x + 1.
Their product = x(x + 1) = x2 + x
By problem x2 + x = 306
⇒ x2 + x – 306 = 0
where x is the smaller integer.
iii) Rohan’s mother is 26 years older than him. The product of their ages after 3 years will be 360 years. We need to find Rohan’s present age.
Answer:
Let the present age of Rohan be x years.
Then age of Rohan’s mother = x + 26
After 3 years:
Age of Rohan would be = x + 3
Rohan’s mother’s age would be = (x + 26) + 3 = x + 29
By problem (x + 3) (x + 29) = 360
⇒ x(x + 29) + 3(x + 29) = 360
⇒ x2 + 29x + 3x + 87 = 360
⇒ x2 + 32x + 87 – 360 = 0
⇒ x2 + 32x – 273 = 0
⇒ x2 + 39x – 7x – 273 = 0
⇒ x (x + 39) – 7 (x + 39) = 0
⇒ (x – 7) (x + 39) = 0
⇒ x = 7 or x = -39 ‘x’ being age cannot be negative.
∴ x = Present age of Rohan = 7 years.
![]()
iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Answer:
Let the speed of the train be x km/h.
Then time taken to travel a distance of distance of 480 km = \(\frac{\text { distance }}{\text { speed }}\) = \(\frac{480}{x}\)
If the speed is 8km/h less, then time needed to cover the same distance would be \(\frac{480}{x-8}\)
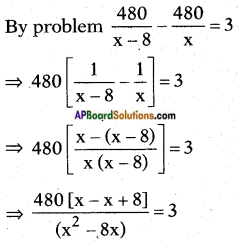
⇒ x2 – 8x = 1280
⇒ x2 – 8x – 1280 = 0
where x is the speed of the train.
