AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 4 Pair of Linear Equations in Two Variables Ex 4.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 4th Lesson Pair of Linear Equations in Two Variables Exercise 4.2
10th Class Maths 4th Lesson Pair of Linear Equations in Two Variables Ex 4.2 Textbook Questions and Answers
Form a pair of linear equations for each of the following problems and find their solution.
Question 1.
The ratio of incomes of two persons is 9 : 7 and the ratio of their expenditures is 4 : 3. If each of them manages to save Rs. 2000 per month, find their monthly income.
Answer:
Given ratio of incomes of two persons = 9 : 7
So let the incomes of each = Rs. 9x and Rs. 7x
and ratio of expenditures = 4 : 3
So let the expenditures of each = 4y and 3y
then earnings of each = (income – expenditure) of each
⇒ 9x – 4y = Rs. 2000 and 7x – 3y = 200
∴ 9x – 4y = 7x – 3y = 2000
⇒ 9x – 7x = 4y – 3y
⇒ y = 2x
now putting y = 2x in 9x – 4y = 2000 we get
9x – 4(2x) = 2000 ⇒ x = 2000
∴ Income of each = 9x = 9(2000) = 18000
and 7x = 7(2000) = 14,000
![]()
Question 2.
The sum of a two digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?
Answer:
Let the digit in units place be x
and the digit in tens place be y
then the value of the number = 10y + x
Number obtained by reversing the digits = 10x + y
By problem,
(10y + x) + (10x + y) = 66
and x – y = 2
⇒ 11x – 11y = 66 and x – y = 2
⇒ x + y = 6 and x – y = 2
Solving these two equations
x + y = 6
x – y = 2
(+) 2x = 8
x = \(\frac{8}{2}\) = 4
Substituting x = 4 in x + y = 6
we get 4 + y = 6 ⇒ y = 2
Substituting x, y values in equations (10y + x) & (10x + y),
We get 10y + x
= 10(2) + 4 = 20 + 4 = 24
and 10x + y = 10(4) + 2
= 40 + 2 = 42
∴ The number is 42 or 24
Thus we have two such numbers.
Question 3.
The larger of two supplementary angles exceeds the smaller by 18°. Find the angles.
Answer:
Let the pair of supplementary angles be x and y [and x > y]
then we have x + y = 180° …… (1)
By problem, x = y + 18°
⇒ x – y = 18° …… (2)
Solving the equations (1) and (2) we get
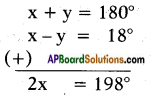
and x = \(\frac{198}{2}\) = 99°
Substituting x = 99° in equation (2) we get
99° – y° = 18°
⇒ y° = 99° – 18 = 81°
∴ The angles are 99° and 81°.
![]()
Question 4.
The taxi charges in Hyderabad are fixed, along with the charge for the distance covered. For a distance of 10 km., the charge paid is Rs. 220. For a journey of 15 km. the charge paid is Rs. 310.
i) What are the fixed charges and charge per km?
ii) How much does a person have to pay for travelling a distance of 25km?
Answer:
Let the fixed charge be = Rs. x.
and the charge per one km = Rs. y.
By problem, x + 10y = 220 x + 15y = 310
Solving (1) and (2) we get

∴ y = \(\frac{-90}{-5}\) = 18
i.e., charge per one km = Rs. 18
Substituting y = 18 in equation (1) we get
x + 10 × 18 = 220
⇒ x = 220 – 180
⇒ x = Rs. 40
∴ Fixed charge = Rs. 40;
Charge per km = Rs. 18.
ii) Now, the charge for travelling a distance of 25 km = 25 × 18
= Rs. 450 + 40
= Rs. 490
Question 5.
A fraction becomes equal to \(\frac{4}{5}\) if 1 is added to both numerator and denominator. If, however, 5 is subtracted from both numerator and denominator, the fraction becomes equal to \(\frac{1}{2}\). What is the fraction?
Answer:
Let the numerator of the fraction = x
and the denominator of the fraction = y
By problem,
\(\frac{x+1}{y+1}\) = \(\frac{4}{5}\) and \(\frac{x-5}{y-5}\) = \(\frac{1}{2}\)
⇒ 5(x + 1) = 4(y + 1) and 2(x – 5) = 1(y – 5)
5x + 5 = 4y + 4 and 2x – 10 = y – 5
⇒ 5x – 4y = 4 – 5 and 2x – y = – 5 + 10
⇒ 5x – 4y = – 1 …… (1)
and 2x – y = 5 …… (2)
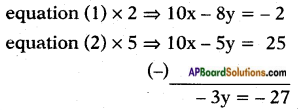
∴ y = \(\frac{-27}{-3}\) = 9
Substituting y = 9 in equation (2) we get
2x – 9 = 5
⇒ 2x = 5 + 9
⇒ 2x = 14 and
x = \(\frac{14}{2}\) = 7
Thus the fraction is \(\frac{x}{y}\) = \(\frac{7}{9}\)
![]()
Question 6.
Places A and B are 100 km apart on a highway One car starts from A and another from B at the same time at different speeds. If the cars travel in the same direction, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Answer:

Let the speed of the car which started from the place A = x kmph
and B = y kmph
Distance travelled by first car in 5h = 5x and in 1h = x
The distance covered by second car in 5h = 5y and in 1h = y
By problem when travelled in same direction,
5x – 5y = 100 ⇒ x – y = 20 …… (1)
and when travelled towards each other
x + y = 100 ……. (2)
Solving (1) and (2),

∴ x = \(\frac{120}{2}\) = 60
Substituting x = 60 in equation (1) we get
60 – y = 20
⇒ y = 60 – 20 = 40 kmph
Thus the speed of the cars are 60 kmph and 40 kmph.
Question 7.
Two angles are complementary. The larger angle is 3° less than twice the measure of the smaller angle. Find the measure of each angle.
Answer:
Let the pair of complementary angles be x° and y° with x° > y°
then x° + y° = 90° and
By problem
x = 2y – 3° ⇒ x – 2y = – 3°
Solving these two equations we get,

∴ y = \(\frac{93}{3}\) = 31°
Substituting y = 31°in x + y = 90° we get
x + 31° = 90°
⇒ x = 90° – 31° = 59°
The angles are 59° and 31°.
![]()
Question 8.
An algebra textbook has a total of 1382 pages. It is broken up into two parts. The second part of the book has 64 pages more than the first part. How many pages are in each part of the book?
Answer:
Let the first part of the book contains x pages
and the second part of the book contains y pages By problem,
x + y = 1382 ….. (1)
y = x + 64 ⇒ x – y = -64 …… (2)
Solving equations (1) and (2) we get

∴ x = \(\frac{1318}{2}\) = 659
Substituting x = 659 in equation (1) we get
659 + y = 1382
⇒ y = 1382 – 659 = 723
∴ The number of pages in the first part = 659
Second part = 723
Question 9.
A chemist has two solutions of hydrochloric acid in stock. One is 50% solution and the other is 80% solution. How much of each should be used to obtain 100 ml of a 68% solution?
Answer:
Let the first solution contains 50% acid.
Second solution contains 80% acid.
Let x ml of 1st solution and y ml of second solution are added.
Then x + y = 100
Acid content in the ‘mix’ is 50% of x + 80% of y = 68%

∴ y = \(\frac{180}{3}\) = 60
Substituting y = 60 in equation (1) we get
x + 60 = 100
⇒ x = 100 – 60 = 40
∴ Quantity of first solution = 40 ml
Quantity of second solution = 60 ml
![]()
Question 10.
Suppose you have Rs. 12000 to invest. You have to invest some amount at 10% and the rest at 15%. How much should be invested at each rate to yield 12% on the total amount invested ?
Answer:
Let the amount to be invested @ 10% be Rs. x
and the amount to be invested @ 15% be Rs. y
By problem x + y = 12000 ……. (1)
Also 10% of x + 15% of y = 12% of 12000
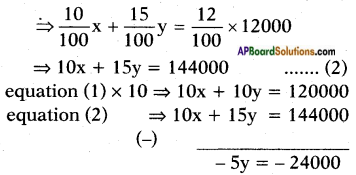
⇒ y = \(\frac{-24000}{-5}\) = Rs. 4800
Substituting y = 4800 in equation (1) we get
x + 4800 = 12000
⇒ x = 12000 – 4800 = 7200
The invested @ 10% = Rs. 7200
@ 15% = Rs. 4800
