AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 1 Real Numbers Ex 1.4 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.4
10th Class Maths 1st Lesson Real Numbers Ex 1.4 Textbook Questions and Answers
Question 1.
Prove that the following are irrational,
i) \(\frac{1}{\sqrt{2}}\)
ii) √3 + √5
iii) 6 + √2
iv) √5
v) 3 + 2√5
Answer:
i) \(\frac{1}{\sqrt{2}}\)
On the contrary, suppose that is a \(\frac{1}{\sqrt{2}}\) rational number;
then \(\frac{1}{\sqrt{2}}\) is of the form where \(\frac{p}{q}\) and q are integers.
∴ \(\frac{1}{\sqrt{2}}\) = \(\frac{p}{q}\)
⇒ \(\frac{\sqrt{2}}{1}\) = \(\frac{q}{p}\)
(i.e.,) √2 is a rational number and it is a contradiction. This contradiction arised due to our supposition that \(\frac{1}{\sqrt{2}}\) is a rational number.
Hence \(\frac{1}{\sqrt{2}}\) is an irrational number.
![]()
ii) Suppose √3 + √5 is not an irrational number.
Then √3 + √5 must be a rational number.
√3 + √5 = \(\frac{p}{q}\), q ≠ 0 and p, q ∈ Z
Squaring on both sides

but √15 is an irrational number.
\(\frac{p^{2}-8 q^{2}}{2 q^{2}}\) is a rational number
(p2 – 8q2, 2q2 ∈ Z, 2q2 ≠ 0)
but an irrational number can’t be equal to a rational number, so our supposition that √3 + √5 is not an irrational number is false.
∴ √3 + √5 is an irrational number.
iii) 6 + √2
To prove: 6 + √2 is an irrational number.
Let us suppose that 6 + √2 is a rational number.
∴ 6 + √2 = \(\frac{p}{q}\), q ≠ 0
⇒ √2 = \(\frac{p}{q}\) – 6
⇒ √2 = Difference of two rational numbers
⇒ √2 = rational number But this contradicts the fact that √2 is an irrational number.
∴ Our supposition is wrong.
Hence the given statement is true.
6 + √2 is an irrational number.
iv) √5
To prove: √5 is an irrational number.
On the contrary, let us assume that √5 is a rational number.
∴ √5 = \(\frac{p}{q}\), q ≠ 0
If p, q have a common factor, on cancelling the common factor let it be
reduces to \(\frac{a}{b}\) where a, b are co-primes.
Now √5 = \(\frac{a}{b}\), where HCF (a, b) = 1
Squaring on both sides we get
⇒ (√5)2 = \(\left(\frac{a}{b}\right)^{2}\)
⇒ 5 = \(\frac{\mathrm{a}^{2}}{\mathrm{~b}^{2}}\)
⇒ 5b2 = a2
⇒ 5 divides a2 and thereby 5 divides 5
Now, take a = 5c
then, a2 = 25c2
i.e., 5b2 = 25c2
⇒ b2 = 5c2
⇒ 5 divides b2 and thereby b.
⇒ 5 divides both b and a.
This contradicts that a and b are co-primes.
This contradiction arised due to our assumption that √5 is a rational number.
Hence our assumption is wrong and the given statement is true, i.e., √5 is an irrational number,
![]()
v) 3 + 2√5
To Prove: 3 + 2√5 is an irrational.
On the contrary, let us assume that 3 + 2√5 is a rational number.
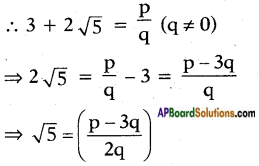
Here p, q being integers we can say that \(\frac{p-3q}{2q}\) is a rational number.
This contradicts the fact that √5 is an irrational number. This is due to our assumption “3 + 2√5 is a rational number”.
Hence our assumption is wrong.
∴ 3 + 2√5 is an irrational number.
Question 2.
Prove that √p + √q is an irrational, where p, q are primes.
Answer:
Given that p, q are primes.
Hence fp and fq are irrationals.
[∵ p, q have no factors other than 1 ∵ they are primes.]
Now √p + √q = sum of two irrational numbers = an irrational number
Hence proved.
