Students can go through AP SSC 10th Class Maths Notes Chapter 7 Coordinate Geometry to understand and remember the concepts easily.
AP State Syllabus SSC 10th Class Maths Notes Chapter 7 Coordinate Geometry
→ The branch of mathematics which deals with points in a coordinate plane is called Coordinate/Analytical geometry.
→ There is a definite one-one correspondence between the position of a point in a plane and a pair of numbers called coordinates.
→ In a Cartesian plane, the position of a point P is determined by two coordinates x and y, where x is the distance of P from Y – axis and y is the distance of P from X – axis. So we denote it by P (x, y).
![]()
→ Signs of coordinates in different quadrants:

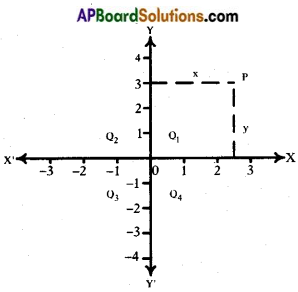
→ The point of intersection of the axes is called the- origin represented by (0, 0).
→ Any point lying on X – axis is denoted by (x, 0) as its y-coordinate is zero.
→ A point on Y – axis is denoted by (0, y) as its x-coordinate is zero.
→ Distance between any two points P(x1, y1) and Q(x2, y2) is given by
PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
![]()
→ Distance between any two points P(x1, 0) and Q(x2, 0) on the X – axis is | x2 – x1 |.
Distance between any two points P(0, y1) and Q(0, y2) on the Y – axis is | y2 – y1 |
→ The coordinates of the point P which divides the line joining of two points (x1, y1) and (x2, y2) internally in the ratio m1 : m2 is
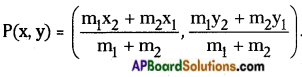
→ The midpoint of a line joining any two points (x1, y1) and (x2, y2) is

→ If the ratio in which ‘P’ divides two points (x1, y1) and (x2, y2) is k : 1, then
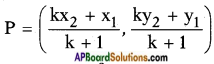
→ The point of concurrence of medians of a triangle is called its centroid.
→ Centroid divides each median in the ratio 2 : 1.
→ If (x1, y1), (x2, y2) and (x3, y3) are the vertices of a triangle, then its centroid is 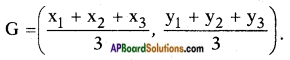
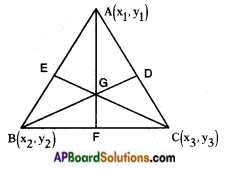
→ The points P, Q on a line segment \(\overline{\mathrm{AB}}\) are said to be the points of trisection, if P and Q divides \(\overline{\mathrm{AB}}\) into three equal points i.e., AP = PQ = QB.
→ If P, Q are points of trisection of \(\overline{\mathrm{AB}}\), then P divides AB in the ratio 1 : 2 and Q divides AB in the ratio 2 : 1.

![]()
→ Area of a triangle AOB formed by the points origin O(0, 0), a point on X – axis A (x, 0) and another point on Y – axis B(0, y) is \(\frac{1}{2}\)xy.
→ If (x1, y1), (x2, y2) and (x3, y3) are the vertices of a triangle, then its area is
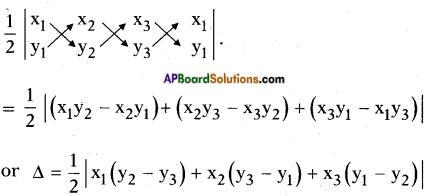
→ If three points are collinear, then the area of the triangle formed by these points is zero.
→ Let A (x1, y1), B (x2, y2) and C (x3, y3) are the vertices of a triangle △ABC, then AB = c; BC = a and AC = b and
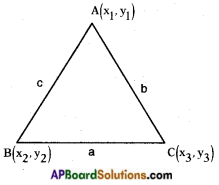
S = \(\frac{a+b+c}{2}\)(semi-perimeter)
Then area of △ABC = \(\sqrt{S(S-a)(S-b)(S-c)}\)
This is called Heron’s formula.
→ Let ax + by + c = 0 represents a straight line; then any pair of coordinates (x1, y1) satisfying the linear equation ax + by + c = 0 is called its solution, i.e., if (x1, y1) is a solution of ax + by + c = 0 then ax1 + by1 + c = 0.
![]()
→ The inclination or angle made by a straight line with positive X-axis is called the slope of the straight line. Slope of a line joining any two points (x1, y1) and (x2, y2) is m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
→ If ‘θ’ is the angle made by a line with X-axis, then slope m = tan θ.