Students can go through AP SSC 10th Class Maths Notes Chapter 2 Sets to understand and remember the concepts easily.
AP State Syllabus SSC 10th Class Maths Notes Chapter 2 Sets
→ Set theory is comparatively a new concept in mathematics.
→ This theory was developed by George Cantor.
→ A well defined collection of objects or ideas is known as “set”.
![]()
→ Well defined means that:
i) All the objects in the set should have a common feature or property.
ii) It should be possible to decide whether any given object belongs to the set or not.
Example or comparision of well defined and not well defined collections:
| Not well defined collections | Well defined collections |
| i) A family of rich persons | i) A family of persons having more than one crore rupees |
| ii) A group of tall students | ii) A group of students, with height 160 cm or more |
| iii) A group of numbers | iii) A group of even natural numbers less than 15 |
→ Some more examples of well defined collections:
i) Vowels of English alphabets, namely a, e, i, o, u.
ii) Odd natural numbers less than 11, namely 1, 3, 5, 7, 9.
iii) The roots of the equation x2 – 3x + 2 = 0, i.e., 1 and 2.
→ Objects, elements and members of a set are synonymous words.
→ Sets are usually denoted by the capital letters like A, B, C, X, Y, Z, etc.
→ An object belonging to a set is known as a member/element/individual of the set.
→ The elements of a set are represented by small case letters,
i.e., a, b, c, , x, y, z, etc.
→ If ‘b’ is an element of a set A, then we say that ‘b’ belongs to A.
→ The word ‘belongs to’ is denoted by the Greek symbol ‘∈’.
→ Thus, in a notation form, ‘b’ belongs to A is written as b ∈ A and ‘c’ does not belong to ‘A’ is written as c ∉ A.
→ Representation of sets: Sets are generally represented by the following two methods.
i) Roster (or) Tabular form
ii) Rule method (or) Set builder form.
→ Roster (or) Tabular form: In this form, all elements of the set are written, separated by commas, within curly brackets.
Example:
i) The set of all natural numbers less than 5 is represented as N = {l,2,3,4}
ii) The set of all letters in the word “JANUARY” is represented as B = {A, J, N, R, U, Y}
Note:
a) In a set notation, order is not important.
b) The elements of a set are generally not repeated in a particular set.
![]()
→ Set builder form (or) Rule method: In this method, a set is described by using a representative and stating the property (or) properties which the elements of the set satisfy, through the representative.
Example:
i) Set of all natural numbers less than 5.
A = {x : x ∈ N, x < 5}
ii) Set of vowels of the English alphabet.
V = {x : x is a vowel in the English alphabet)
Note: It may be observed that we describe the set by using a symbol (x or y or z etc.) for elements of the set.
→ Types of set:
→ Empty set (or) Null set (or) Void set: A set, which does not contain any element is called an empty set (or) a null set (or) a void set.
→ Empty set is denoted by ∅ (or) { }

Example :
A = (x : x is a natural number smaller than 1}
B = {x : x2 – 2 = 0 and x is a rational number}
C = (x : x is a man living on the moon}
Note: ∅ and { 0 } are two different sets. {0} is a set containing the single element ‘0’ while { } is a null set.
→ Singleton set: A set consisting of a single element is called a singleton set.
Examples:
{ 0 }, {- 7} are singleton sets.

→ Finite set: A set which is possible to count the number of elements of that set is called finite set.
Example – 1 : The set {3, 4, 5, 6} is a finite set, because it contains a definite number of elements i.e., only 4 elements.
Example – 2 : The set of days in a week is a finite set.

Example – 3 : An empty set, which does not contain any element (no element) is also a finite set.
→ Infinite set: A set whose elements cannot be listed, that type of set is called infinite set.

Example : i) B = {x : x is an even number}
ii) J = {x : x is a multiple of 7}
iii) The set of all points in a plane. s|s A set is infinite if it is not finite.
![]()
→ Equal sets: Two sets are said to be equal, if they have exactly the same elements.
For example: The set A and B are having same elements i.e., watch, ring, flower are said to be equal sets.

→ Cardinal number: The number of elements in a set is called the cardinal number of the set.
Example: Consider the finite set A = {1, 2, 4}
Number of elements in set ‘A’ is 3.
It is represented by n(A) = 3
→ Universal set: A set which consists of all the sets under consideration (or) discussion is called the universal set. (or) A set containing all objects or elements and of which all other sets or subsets.
It is usually denoted by ∪ (or) μ.
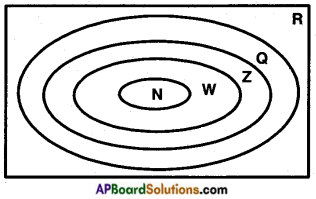
The universal set is usually represented by rectangles.
Example:
i) The set of real numbers is universal set for number theory.
Here ‘R’ is a universal set.
ii) If we want to study various groups of people of our state, universal set is the set of all people in Andhra Pradesh.
→ Subset: If every element of first set (A) is also an element of second set (B), then first set (A) is said to be a subset of second set (B).
→ It is represented as A ⊂ B.
Example :
Set A = {2, 4, 6, 8} is a subset of .
Set B = {1,2, 3, 4,5, 6, 7, 8}
![]()
→ Empty set is a subset of every set.
→ Every set is a subset of itself.
→ Consider ‘A’ and ‘B’ are two sets, if A ⊂ B and B ⊂ A ⇔ A = B.
→ A set doesn’t change if one or more elements of the set are repeated.
→ If A ⊂ B, B ⊂ C ⇒ A ⊂ C.
→ Venn Diagrams: Venn-Euler diagram or simply Venn diagram is a way of representing the relationships between sets.
→ These diagrams consist of rectangles and closed curves usually circles.
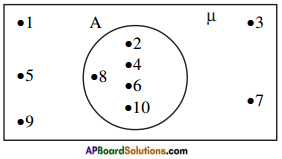
Example: Consider that U = {1, 2, 3, ……, 10} is
the universal set of which, A = {2, 4, 6, 8, 10} is a subset.
Then the Venn diagram is as:
→ Basic operations on sets: In sets, we define the operations of union, intersection and difference of sets.
→ Union of sets: The union of two or more sets is the set of all those elements which are either individual (or) both in common.
→ In symbolic form, union of two sets A and B is written as A ∪ B and usually read as “A union B”.
→ Set builder form of A ∪ B is A ∪ B = (x : x ∈ A or x ∈ B}
→ The union of the sets can be represented by a Venn diagram as shown (shaded portion).

→ It is evident from the definition that A ⊆ A ∪ B; B ⊆ A ∪ B.
→ Roster form of union of sets : Let A = {a, e, i, o, u} and B = (a, i, u} then A ∪ B = {a, e, i, o, u} ∪ { a, i, u} = {a, e, i, o, u}
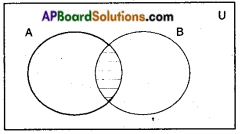
→ Intersection of sets: The intersection of two sets A and B is the set of all those elements which belong to both A and B.
→ We denote intersection by A ∩ B.
→ We read A ∩ B as “A intersection B”.
→ Symbolically, we write A ∩ B = (x : x ∈ A and x ∈ B}
→ The intersection of A and B can be illustrated in the Venn diagram as shown in the shaded portion in the adjacent figure.
![]()
→ The intersection of A and B can be illustrated in the Roster form:
If A = {5, 6, 7, 8} and B = {7, 8, 9, 10} then A ∩ B = {7, 8}
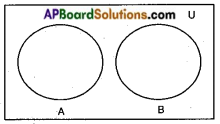
→ Disjoint set: Consider A and B are two finite sets and if there are no common element in both A and B. Such set is known as disjoint set (or A ∩ B = ∅).
(or)
Two sets (finite) are said to be disjoint sets if they have no common elements. That is if the intersection of two sets is a null set they are disjoint sets.
→ The disjoint sets can be represented by means of the Venn diagrams as shown in the adjacent figure.
→ Difference of sets: The difference of sets A and B is the set of elements which belong to ‘A’ but do not belong to ‘B’.
→ We denote the difference of A and B by A – B or simply “A minus B”.
→ Set builder form of A – B is (x : x ∈ A and ∉ B}
→ Venn-diagram of A – B is
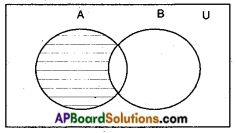
→ Venn-diagram of B – A is
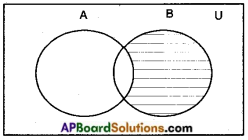
→ A – B ≠ B – A
→ Fundamental theorem on sets:
If A and B are any two sets then n (A ∪ B) = n (A) + n (B) – n (A ∩ B) where
n (A ∪ B) = number of elements in the set (A ∪ B), also called cardinal number of A ∪ B
n (A) = number of elements in the set A also called cardinal number of A
n (B) = number of elements in the set B also called cardinal number of B