Students can go through AP SSC 10th Class Maths Notes Chapter 12 Applications of Trigonometry to understand and remember the concepts easily.
AP State Syllabus SSC 10th Class Maths Notes Chapter 12 Applications of Trigonometry
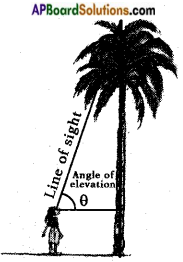
→ If a person is looking at an object then the imaginary line joining the object and the eye of the observer is called the line of sight or ray of view.
→ An imaginary line parallel to earth surface and passing through the point of observation is called the horizontal.
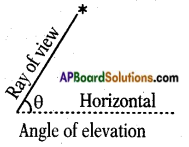
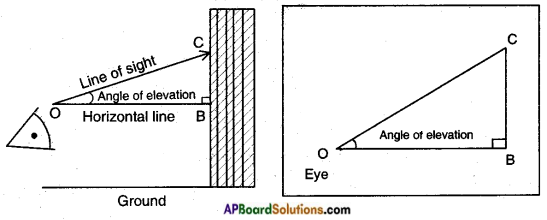
→ If the line of sight is above the horizontal then the angle between them is called “angle of elevation”.
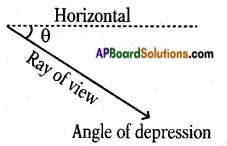
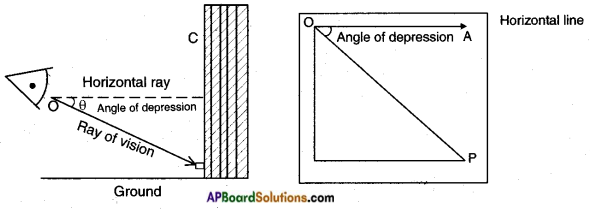
→ If the line of sight is below the horizontal then the angle between them is called the angle of depression.
→ Useful hints to solve the problems:
- Draw a neat diagram of a right triangle or a combination of right triangles if necessary.
- Represent the data given on the triangle.
- Find the relation between known values and unknown values.
- Choose appropriate trigonometric ratio and solve for the unknown.
→ The height or length of an object or the distance between two distant objects can be determined with the help of trigonometric ratios.
→ To use this application of trigonometry, we should know the following terms.
→ The terms are Horizontal line, Line of Sight, Angle of Elevation and Angle of Depression.
→ Horizontal line: A line which is parallel to earth from observation point to object is called “horizontal line”.
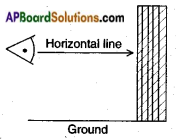
→ Line of Sight (or) Ray of Vision: The line of sight is the line drawn from the eye of an observer to the point in the object viewed by the observer.
→ Angle of Elevation: The line of sight is above the horizontal line then angle between the line of sight and the horizontal line is called “angle of elevation”.
Note:
- If the angle of observer moves towards the perpendicular line (pole/tree/ building), then angle of elevation increases and if the observer moves away from the perpendicular line (pole/tree/building), then angle of elevation decreases.
- If height of tower is doubled and the distance between the observer and foot of the tower is also doubled, then the angle of elevation remains same.
- If the angle of elevation of sun above a tower decreases, then the length of shadow of a tower increases.
→ Angle of Depression: The line of sight is below the horizontal line then angle between the line of sight and the horizontal line is called angle of depression.
Note:
- The angle of elevation and depression are always acute angles.
- The angle of elevation of a point P as seen from a point ‘O’ is always equal to the angle of depression of ‘O’ as seen from P.
→ Points to be kept in mind:
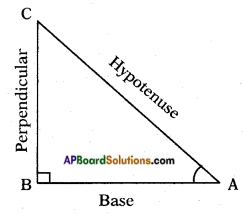
I. Trigonometric ratios in a right triangle:

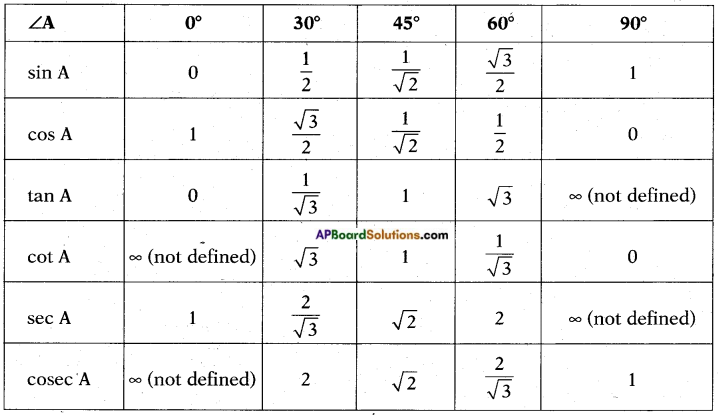
II. Trigonometric ratios of some specific angles:
→ Solving Procedure:
When we want to solve the problems of height and distances, we should consider the following :
- All the objects such as tower, trees, buildings, ships, mountains, etc. shall be considered as linear for mathematical convenience.
- The angle of elevation or angle of depression is considered with reference to the horizontal line.
- The height of the observer is neglected, if it is not given in the problem.
- To find heights and distances, we need to draw figures and with the help of these figures we can solve the problems.