Students can go through AP Inter 2nd Year Physics Notes 5th Lesson Electrostatic Potential and Capacitance will help students in revising the entire concepts quickly.
AP Inter 2nd Year Physics Notes 5th Lesson Electrostatic Potential and Capacitance
→ Electric potential is defined as the work done in bringing a unit positive test charge from infinity to that point against the electric field.
→ Potential difference between two points in an electric field is defined as the workdone per unit positive test charge in moving it from one point to the other against the electric field.
→ Electric potential due to a point charge V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)
→ Electrostatic potential energy of two charges q1 and q2; = U(q1 q2) = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}}\)
→ Electrostatic potential energy of system of charges is given by = U(q1, q2, q3) = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{\mathrm{q}_1 \mathrm{q}_2}{\mathrm{r}_1}+\frac{\mathrm{q}_2 \mathrm{q}_3}{\mathrm{r}_2}+\frac{\mathrm{q}_3 \mathrm{q}_1}{\mathrm{r}_3}\right]\)
![]()
→ Potential due to an electric dipole V = \(\frac{P \cos \theta}{4 \pi \varepsilon_0 r^2}\)
→ Equipotential surface is a surface with a constant value of potential at all points on the surface.
→ Relation between electric field and potential is given by E = \(-\frac{\delta \mathrm{V}}{\delta \mathrm{l}}=+\frac{|\delta \mathrm{V}|}{\delta l}\)
→ Potential energy of a dipole in an external field U(θ) = PE(cos θ0 – cosθ1)
→ The dipole moment per unit volume is called polarisation and is denoted by P.
→ Capacitor is a device, which stores high charge at low potential C = \(\frac{Q}{V}\)
→ Capatictance of parallel plate capacitor C = \(\frac{\varepsilon_0 \mathrm{~A}}{\mathrm{~d}}\)
→ For series connection, \(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\frac{1}{\mathrm{C}_3}+\cdots \cdots\)
→ For parallel connection, C = C1 + C2 + C3 + ……
→ Energy U stored in a capacitor of capaÇitance C with charge Q and voltage V is
U = \(\frac{1}{2} \mathrm{CV}^2=\frac{\mathrm{Q}^2}{2 \mathrm{C}}=\frac{\mathrm{QV}}{2}\)
→ A dielectric gets polarised when place in an enternal electric field (E0). Due to polarisation, an induced electric field Ei is developed inside the dielectric, in a direction opposite to E0.
![]()
Net electric field inside the dielectric is E = E0 – Ei = \(\frac{E_0}{\mathrm{~K}}\)
→ Van De Graaff Generator is a machine that can build high voltages (few million volts). The resulting large electric fields are used to accelerate charged particles (electrons, protons, ions) to high energies.
Formulae
→ Line integral of electric field is given by
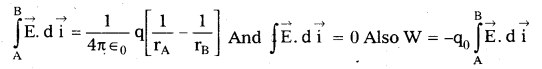
→ PD between two points A and B is .
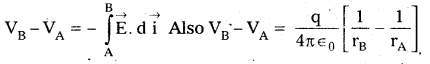
→ Electric potential due to a point charge q is V = \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{q}}{\mathrm{r}}\)
→ Eletric potential due to a system of charges V = \(\frac{1}{4 \pi \epsilon_0} \sum_{i=1}^n \frac{q_i}{r_i}\)
→ Electic potential at any point due to an elctric dipole V = \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{P} \cos \theta}{\left(\mathrm{r}^2-\mathrm{a}^2 \cos ^2 \theta\right)}\)
→ E = \(\frac{-\mathrm{dv}}{\mathrm{dr}}\)
![]()
→ In air C = \(\frac{\epsilon_0 \mathrm{~A}}{\mathrm{~d}}\) In medium C = \(\frac{\mathrm{k} \in_0 \mathrm{~A}}{\mathrm{~d}}\)
→ Capacitance of parallel plate capacitor, whan a diclectric slab partially fills the space between plates. C = \(\frac{\epsilon_0 \cdot A}{d-t\left(1-\frac{1}{k}\right)}\)
→ For spherical capacitor C = \(4 \pi \epsilon_0 \frac{a b}{b-a}\)
→ For cylindrical capacitor C = \(\frac{2 \pi \epsilon_0 l}{\log _e \frac{b}{a}}\)
→ When capacitors are joined together to share charges, then the common potential V is
V = \(\frac{\mathrm{C}_1 \mathrm{~V}_1+\mathrm{C}_2 \mathrm{~V}_2+\mathrm{C}_3 \mathrm{~V}_3+\ldots \ldots}{\mathrm{C}_1+\mathrm{C}_2+\mathrm{C}_3+\ldots \ldots}\)