AP Inter 2nd Year Physics Important Questions Chapter 8 Magnetism and Matter

Students get through AP Inter 2nd Year Physics Important Questions 8th Lesson Magnetism and Matter which are most likely to be asked in the exam.

AP Inter 2nd Year Physics Important Questions 8th Lesson Magnetism and Matter

Very Short Answer Questions

Question 1.
A magnetic dipole placed in a magnetic field experiences a net force. What can you say about the nature of the magnetic field ?
Answer:
The nature of the magnetic field is uniform, magnetic dipole (bar magnet) experiences a net force (or torque).

Question 2.
Do you find two magnetic field lines intersecting ? Why ?
Answer:
Two magnetic field lines never intersect. If they intersect, at the point of intersection the field can have two directions. This is impossible. So, two field lines never intersect.

Question 3.
What happens to the compass needles at the Earth’s poles ? [T.S. Mar. 17; IPE 2014]
Answer:
At the Earth poles, the magnetic field lines are converging or diverging,vertically so that the horizontal component is negligible. Hence, the compass needle can point along any direction.

Question 4.
What do you understand by the ‘magnetisation’ of a sample ? Give its SI unit. [IPE 2016 (AP)]
Answer:
Magnetisation (M) of a sample is equal to its net magnetic moment per unit volume.
Magnetisation, M = \(\frac{m_{n e t}}{V}\), SI unit of magnetisation is Am^-1.

Question 5.
What is the magnetic moment associated with a solenoid ? [IPE 2016 (TS)]
Answer:
The magnitude of magnetic moment of the solenoid is, M = n × 2l × i × πa²
where, ‘n’ is number of turns, ‘2l’ is length of the solenoid, ‘i’ is current passing through coil, and ‘a’ is area of cross section of solenoid.

Question 6.
What are the units of magnetic moment, magnetic induction and magnetic field ? [IPE 2016 (AP), (TS)]
Answer:
The unit of magnetic moment (M) is ampere-meter² (Am²).
The unit of magnetic induction (B) is tesla (T) or N/A-m.
The unit of magnetic field (B) is tesla.

Question 7.
Magnetic lines form continuous closed loops. Why ? [T.S. 2017; IPE 2016(AP)]
Answer:
Magnetic lines are imaginary lines. Within the magnet, they move from south pole to north pole and outside the magnet they move from north pole to south pole. Hence, magnetic lines form continuous closed loops.

Question 8.
Define magnetic declination. [IPE 2016 (TS)]
Answer:
Magnetic declination at a place is the angle between magnetic meridian and geographic meridian at that place.

Question 9.
Define magnetic inclination or angle of dip. [A.P. Mar. 17; A.P. & T.S. 2015 (TS), 14]
Answer:
Magnetic inclination at a place is the angle between direction of total strength of earth’s magnetic field and horizontal line in magnetic meridian.

Question 10.
Classify the following materials with regard to magnetism: Manganese, Cobalt, Nickel, Bismuth, Oxygen, Copper. [T.S. 2015, 2016 (TS); A.P. Mar. 17]
Answer:
Manganese …………. Paramagnetic
Cobalt ………….. Ferromagnetic
Nickel …………….. Ferromagnetic
Bismuth ……………. Diamagnetic
Oxygen ………………. Paramagnetic
Copper …………………. Diamagnetic

Question 11.
The force between two magnet poles separated by a distance ‘d’ in air is ‘F’. At what distance between them does the force become doubled ?
Answer:
Force between two magnetic poles, F₁ = F;
Distance between two magnetic poles, d₁ = d
Force between two magnetic poles increased by double F₂ = 2F
Distance between two magnetic poles, d₂ = ?
From Coulombs law, F₁d₁² = F₂ d₂²
Fd² = 2 F d₂²
⇒ d₂² = \(\frac{\mathrm{d}^2}{2}\)
d₂ = \(\frac{\mathrm{d}}{\sqrt{2}}\)

Question 12.
If B is the magnetic field produced at the centre of a circular coil of one turn of length L carrying current I then what is the magnetic field at the centre of the same coil which is made into 10 turns ?
Answer:
For first circular coil; B₁ = B, n₁ = 1; I₁ = I; a₁ = \(\frac{\mathrm{L}}{2 \pi}\)
For second circular coil, B₂ = ? n₂ = 10; I₂ = I; a₂ = \(\frac{\mathrm{L}}{2 \pi}\)
As B = \(\frac{\mu_0 \mathrm{n} \mathrm{Ia}^2}{2 \mathrm{r}}\), B ∝ n.
\(\frac{\mathrm{B}_2}{\mathrm{~B}_1}=\frac{\mathrm{n}_2}{\mathrm{n}_1}\)
\(\frac{\mathrm{B}_2}{\mathrm{~B}}=\frac{10}{1}\)
∴ B₂ = 10 B

Question 13.
If the number of turns of a solenoid is doubled, keeping the other factors constant, how does the magnetic field at the axis of the solenoid change ?
Answer:
B₁ = B (say); n₁ = n; n₂ = 2n; B₂ = ?
Magnetic field at the centre of a solenoid is given by B = \(\frac{\mu_0 \mathrm{nI} \mathrm{a}^2(2 l)}{2 \mathrm{r}^3}\)
As I, a², 2l and r are constants, B ∝ n
⇒ \(\frac{\mathrm{B}_2}{\mathrm{~B}_1}=\frac{\mathrm{n}_2}{\mathrm{n}_1} \Rightarrow \frac{\mathrm{B}_2}{\mathrm{~B}}=\frac{2 \mathrm{n}}{\mathrm{n}}\)
∴ B₂ = 2B

Question 14.
A closely wound solenoid of 800 turns and area of cross section 2.5 × 10^-4 m² carries a current of 3.0A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment ?
Answer:
Here n = 800, a = 2.5 × 10^-4 m², I = 3.0 A
A magnetic field develop along the axis of the solenoid. Therefore the current carrying solenoid behaves like a bar magnet
m = N IA = 800 × 3.0 × 2.5 × 10^-4
= 0.6 Am² along the axis of solenoid.

Short Answer Questions

Question 1.
Compare the properties of para, dia and ferromagnetic substances.
Answer:
Diamagnetic substances
a) When these materials placed in a magnetic field, they are magnetised feebly in the opposite direction to the applied external field.
b) When a rod of diamagnetic material is suspended freely in a uniform magnetic field, it comes to rest in the perpe-ndicular direction to the magnetic field.
c) When they are kept in a non-uniform magnetic field, they move from the region of greater field strength to the region of less field strength.
d) The relative permeability is less than 1. μ_r < 1 and negative.
e) The susceptibility (χ) is low and negative.
E.g.: Copper, Silver, Water, Gold, Antimony, Bismuth, Mercury, Quartz Diamond etc.

Paramagnetic substances
a) When these materials placed in a magnetic field, they are magnetised feebly in the direction of the applied magnetic field.
b) When a rod of paramagnetic material is suspended freely in a uniform magnetic field, it comes to rest in the direction of the applied magnetic field.
c) When they are kept in a non-uniform magnetic field„they move from the region of less field strength to the region of greater field strength.
d) The relative permeability is greater than 1. μ_r > 1 and positive.
e) The susceptibility (χ) is small and positive.
E.g.: Aluminium, Magnesium, Tungsten, Platinum, Mang-anese, liquid oxygen, Ferric chloride, Cupric chloride etc.

Ferromagnetic substances
a) When these materials placed in a magnetic field,they are magnetised strongly in the direction of the applied external field.
b) When a rod of ferromagnetic material is suspended freely in a uniform magnetic field, it comes to rest in the direction of the applied magnetic field.
c) When they are kept in a non-uniform magnetic field they move from the regions of lesser (magnetic field) strength to the regions of stronger (magnetic field) strength.
d) The relative permeability is much greater than 1. μ_r >> 1 and positive.
e) The susceptibility (χ) is high and positive.
E.g.: Iron, Cobalt, Nickel, Gadolinium and their alloys.

Question 2.
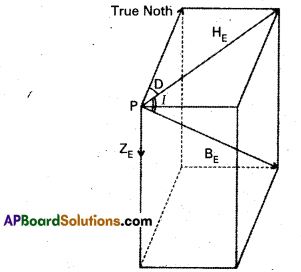
Explain the elements of the Earth’s magnetic field and draw a sketch showing the relationship between the vertical component, horizontal component and angle of dip.
Answer:
The magnetic field of the earth at a point on its surface can be specified by the declination D, the angle of dip or the inclination I and the horizontal component of the earth’s field HE. These are known as the elements of the earth’s magnetic field.

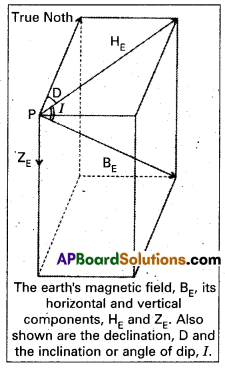
Explanation:

1. The total magnetic field at P can be resolved into a horizontal component H_E and a vertical component Z_E.
2. The angle that B_E makes with H_E is the angle of dip, I.
3. Representing the vertical component by Z_E, we have
   Z_E= B_E Sin I
   H_E = B_E Cos I
   Which gives Tan I = \(\frac{\mathrm{Z}_{\mathrm{E}}}{\mathrm{H}_{\mathrm{E}}}\)

Question 3.
Define magnetic susceptibility of a material. Name two elements one having positive susceptibility and other having negative susceptibility.
Answer:

1. Susceptibility: When a material is placed in a magnetic field, the ratio of the intensity of magnetization acquired by it to the intensity of the applied magnetic field is called its susceptibility.
   Suspectibility χ = \(\frac{\text { Intensity of magnetisation, } \mathrm{I}}{\text { Applied magnetic field, } \mathrm{H}}\)
2. The susceptibility of a material represents its ability to get magnetism.
3. Susceptibility is a dimension less quantity.
4. Relation between μ_r and χ :
   a) Suppose that material is placed in a magnetic field of intensity H. Let I be the intensity of magnetisation acquired by it.
   b) Then the magnetic induction within the material is
   B = μ₀H + μ₀I ⇒ \(\frac{\mathrm{B}}{\mathrm{H}}\) = μ₀[1 + \(\frac{\mathrm{I}}{\mathrm{H}}\)]
   ⇒ μ = μ₀[1 + χ] ⇒ \(\frac{\mu}{\mu_0}\) = 1 + χ
   ∴ μ_r = 1 + χ [∵μ_r = \(\frac{\mu}{\mu_0}\)]
5. Negative susceptibility (χ) of diamagnetic elements are Bismuth (-1.66 × 10^-5) and copper (-9.8 × 10^-6).
6. Positive susceptibility of paramagnetic elements are Aluminium (2.3 × 10^-5) and oxygen at STP (2.1 × 10^-6).
7. Large and positive susceptibility of Ferromagnetic elements are Cobalt and Nickel.

Question 4.
Derive an expression for magnetic field induction on the equatorial line of a barmagnet. [Board Model Paper]
Answer:
At a point on equatorial line: Let us consider a point ‘P’ at a distance ‘d’ on the equatorial line from the centre of a bar magnet.

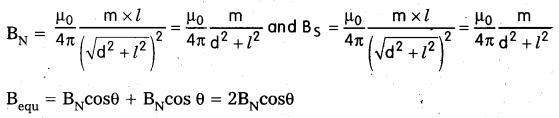
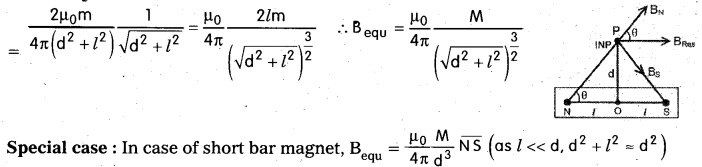
Qeustion 5.
What do you understand by “hysteresis” ? How does this propertry influence the choice of materials used in different appliances where electromagnets are used ?
Answer:

1. Cycle of magnetisation : When a ferromagnetic specimen is slowly magnetised, the intensity of magnetisation varies with magnetic field through a cycle is called cycle of magnetisation.
2. Hysterisis : The lagging of intensity of magnetisation (I) and magnetic induction (B) behind magnetic field intensity (H) when a magnetic specimen is subjected to a cycle of magnetisation is called hysterisis.
3. Retentivity : The value of I for which H = 0 is called retentivity or residual magnetism.
4. Coercivity: The value of magnetising force required to reduce I is zero in reverse direction of H is called coercive force or coercivity.
5. Hysterisis curve : The curve represents the relation between B or I of a ferromagnetic material with magnetising force or magnetic intensity H is known as Hysterisis curve.
6. Explanation of hysterisis loop or curve :
   a) In fig, a closed curve ABCDEFA in H – I plane, called hysteris loop is shown in fig.
   
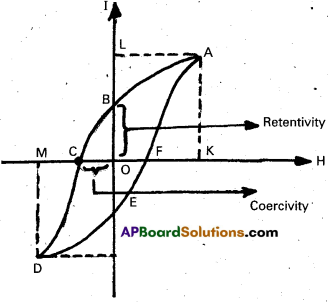
   b) When ferromagnetic specimen is slowly magnetised, I increases with H.
   c) Part OA of the curve shows that I increases with H.
   d) At point A, the value I becomes constant is called saturation value.
   e) At B, I has some value while H is zero.
   f) In fig. BO represents retentivity. and OC represents coercivity.
7. Uses : The properties of hysterisis curve, i.e., saturation, retentivity, coercivity and hysterisis loss help us to choose the material for specific purpose.
   1. Permanent magnets : A permanent magnet should have both large retentivity and large coercivity. Permanent magnets are used in galvanometers, voltmeres, ammeters, etc.
   2. An electromagnet core : The electromagnet core material should have maximum induction field B even with small fields H, low hysterisis loss and high initial permeability.
   3. Transformer cores, Dynamocore, Chokes, Telephone diaphragms: The core material should have high initial permeability, low hysterisis loss and high specific resistance to reduce eddy currents. Soft iron is the best suited material.

Question 6.
Prove that a bar magnet and a solenoid produce similar fields.
Answer:
Bar magnet produce similar field of Solenoid :

1. We know that the current loop acts as a magnetic dipole. According to Ampere’s all magnetic phenomena can be explained in terms of circulating currents.
2. Cutting a bar magnet is like a solenoid. We get two similar solenoids with weaker magnetic properties.
3. The magnetic field lines remain continuous, emerging from one face of solenoid and entering into other face of solenoid.
4. If we were to move a small compass needle in the neighbourhood of a bar magnet and a current carrying solenoid, we would find that the deflections of the needle are similar in both cases as shown in diagrams.
   
   
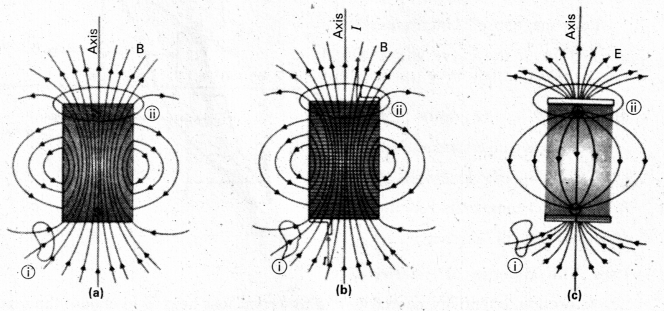
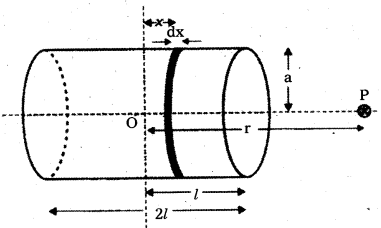
   The axial field of a finite solenoid in order to demonstrate its similarity to that of a bar magnet
5. The magnetic field at point P due to bar magnet in the form of solenoid is B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 m}{r^3}\)
6. The total magnetic field, at a point P due to solenoid is given by
   B = \(\frac{\mu_0 \mathrm{n} \mathrm{I}}{2} \frac{\mathrm{a}^2}{\mathrm{r}^3}(2 l)=\frac{\mu_0}{4 \pi} \frac{2 \mathrm{n}(2 l) \mathrm{I} \pi \mathrm{a}^2}{\mathrm{r}^3}\)
7. The magnitude of the magnetic moment of the solenoid is, m = n(2l) I (πa²).
   ∴ B = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{~m}}{\mathrm{r}^3}\)
8. Therefore, magnetic moment of a bar magnet is equal to magnetic moment of an equivalent solenoid that produces the same magnetic field.

Question 7.
A small magnetic needle is set into oscillations in a magnetic field B obtain an expression for the time period of oscillation.
Answer:
Expression for time period of oscillation :

1. A small compass needle (magnetic dipole) of known magnetic moment m and moment of Inertia i is placing in uniform magnetic field B and allowing it to oscillate in the magnetic field.
2. This arrangement is shown in Figure.
3. The torque on the needle is τ = m × B
4. In magnitude τ = mB sin θ.
   Here τ is restoring torque and θ is the angle between m and B.
5. Therefore, in equilibrium i \(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) = – mB sinθ. Negative sign with mB sin0 implies that restoring torque is in opposition to deflecting torque.
   
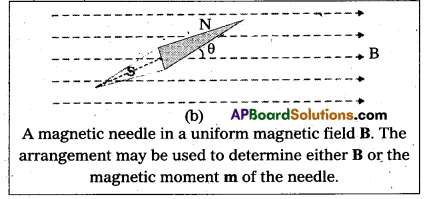
6. For small values of o in radians, we approximate sinθ ≃ θ and get \(i \frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) ≃ – mBθ
   \(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2} \approx \frac{-\mathrm{mB}}{\mathcal{j}} \theta\) …………….. (1)
   This represents a simple harmonic motion. .
7. From defination of simple harmonic motion, we have \(\frac{\mathrm{d}^2 \theta}{\mathrm{dt}^2}\) = – ω²θ …………… (2)
   From equation (I) and (II), we get ⇒ ω² = \(\frac{\mathrm{mB}}{\mathcal{J}}\)
   ∴ ω = \(\sqrt{\frac{\mathrm{mB}}{\mathcal{J}}}\)
8. Therefore, the time period is T = \(=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{\mathcal{J}}{\mathrm{mB}}}\)

Qeustion 8.
A bar magnet, held horizontally, is set into angular oscillations in the Earth’s magnetic field. It has time periods T₁ and T₂ at two places, where the angles of dip are θ₁ and θ₂ respectively. Deduce an expression for the ratio of the resultant magnetic fields at the two places.
Answer:

1. Suppose, the resultant magnetic fields is to be compared at two places A and B.
2. A barmagnet, held horizontally at A and which is set into angular oscillations in the Earth’s magnetic field.
3. Let time period of a bar magnet at place A’ is T₁ and angular displacement or angle of dip is θ₁.
4. As the bar magnet is free to rotate horizontally, it does nqt remain vertical component (B₁ sin θ₁). It can have only horizontal component (B₁ cosθ₁).
5. The time period of a bar magnet in uniform magnetic field is given by T = 2π \(\sqrt{\frac{\mathrm{I}}{\mathrm{mB}_{\mathrm{H}}}}\)
   
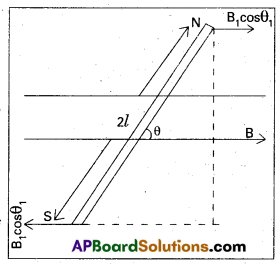
6. Now, in this case T = T₁ and B_H = B₁Cosθ₁
7. Therefore time period of a bar magnet at place ‘A’ is given by
   T₁ = 2π \(\sqrt{\frac{\mathrm{I}}{\mathrm{mB}_1 \cos \theta_1}}\) …………… (1) Where I is moment of Inertia of a barmagnet and m is magnitude of magnetic moment.
8. Similarly, the same bar magnet is placed at B and which is set into angular oscillations in the earth’s magnetic field.
9. Let time period of a bar magnet at place B is T₂ and angle of dip is θ₂.
10. Since horizontal component of earths field at B is B_H = B₂ cos θ₂, time period,
    T₂ = 2π \(\sqrt{\frac{\mathrm{I}}{\mathrm{mB}_2 \cos \theta_2}}\) ………………… (2)
11. Dividing equation (1) by equation (2), we get \(\frac{T_1}{T_2}=\sqrt{\frac{\mathrm{mB}_2 \cos \theta_2}{\mathrm{mB}_1 \cos \theta_1}}\)
    Squaring on both sides, we have \(\frac{\mathrm{T}_1^2}{\mathrm{~T}_2^2}=\frac{\mathrm{B}_2 \cos \theta_2}{\mathrm{~B}_1 \cos \theta_1}\)
12. But B₁ = μ₀H₁, and B₂ = μ₀H₂
    \(\frac{\mathrm{T}_1^2}{\mathrm{~T}_2^2}=\frac{\mu_0 \mathrm{H}_2 \cos \theta_2}{\mu_0 \mathrm{H}_1 \cos \theta_1} \)
13. Therefore, \(\frac{\mathrm{H}_1}{\mathrm{H}_2}=\frac{\mathrm{T}_2^2 \cos \theta_2}{\mathrm{~T}_1^2 \cos \theta_1}\)
14. By knowing T₁, T₂ and θ₁, θ₂ at different places A and B, we can find the ratio of resultant magnetic fields.

Question 9.
Obtain Gauss’ Law for magnetism and explain it.
Answer:
Gauss law for Magnetism :

1. According to Gauss’s law for magnetism, the net magnetic flux (Φ_B) through any closed surface is always zero.
2. The law implies that the no. of magnetic field lines leaving any closed surface is always equal to the number of magnetic field lines entering it.
3. Suppose a closed surface S is held in a uniform magnetic field B. Consider a small vector area element ∆S of this surface as shown in figure.
4. Magnetic flux through this area element is defined as ∆Φ_B = B. ∆S. Then the net flux Φ_B, is,
   Φ_B = \(\sum_{\text {all }} \Delta \phi_B=\sum_{\text {all }} \text { B. } \Delta \mathrm{S}=0\)
5. If the area elements are really small, we can rewrite this equation as
   Φ_B = \(\oint\)B.ds = 0 …………………. (I)
   
6. Comparing this equation with Gauss’s law of electrostatics i.e., electric flux through a closed surface S is given by
   Φ_E = \(\oint \text { E. } \Delta S=\frac{q}{\varepsilon_0}\) …………….. (II) Where q is the electric charge enclosed by the surface.
7. In an electric dipole were enclosed by the surface equal and opposite charges in the dipole add upto zero. Therefore, Φ_E would be zero.
8. The fact that Φ_B = 0 indicates that the simplest magnetic element is a dipole or current loop.
9. The isolated magnetic poles, called magnetic monopoles are not known to exist.
10. All magnetic phenomena can be explained interms of an arrangement of magnetic dipoles and /or current loops.
11. Thus corresponding to equation (II) of Gauss’s theorem in electrostatics, we can visualize equation (I) as
    Φ_E = \(\int_S\) B . dS = μ₀ (m) + μ₀ (-m) = 0 where m is strength of N-pole and -m is strength of
    S – pole of same magnet.
12. The net magnetic flux through any closed surface is zero.

Question 10.
What are ferromagnetic materials ? Give examples. What happens to a ferromagnetic material at curie temperature ? [IPE 2015 (TS)]
Answer:
Ferro magnetic substances : (a) These are strongly attracted by magnet, (b) Susceptibility is large, positive and temperature dependent, (c) Relative permeability, μ_r > > 1 (d) Atoms have permanent dipole moments which are organised in domains. Ex: Iron, Cobalt, Nickel

Curie temperature : The temperature above which a ferro magnetic substance changes in to para magnetic substance changes in to para magnetic substance is called curie temperature.

Problems

Question 1.
A coil of 20 turns has an area of 800 mm² and carries a current of 0.5A. If it is placed in a magnetic field of intensity 0.3T with its plane parallel to the field, what is the torque that it experiences ? ,
Answer:
n = 20; A = 800 mm² = 800 × 10^-6 m²; i = 0.5A; B = 0.3T; θ = 0°.
When the plane parallel to the field,
T = Bin A cos θ = 0.3 × 0.5 × 20 × 800× 10^-6 × cos 0°
∴ τ = 2.4 10^-3 Nm

Question 2.
In the Bohr atom model the electrons move around the nucleus in circular orbits. Obtain an expression the magnetic moment (p) of the electron in a Hydrogen atom in terms of its angular momentum L.
Answer:
Consider an electron of charge e, moves with constant speed v in a circular orbit of radius ‘r’ in Hydrogen atom as shown in fig.

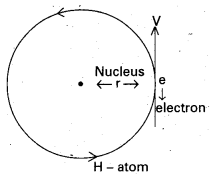
The current constitute by revolving electron in circular motion around a nucleus, I = \(\).
Time period of orbiting electron, T = \(\frac{2 \pi \mathrm{r}}{\mathrm{v}}\) ⇒ I = \(\frac{e}{\frac{2 \pi r}{v}}=\frac{e v}{2 \pi r}\)
orbital magnetic moment, μ = IA = I (πr²)
⇒ μ = \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}}\) (πr²) = \(\frac{\mathrm{evr}}{2}\)
μ = \(\frac{\mathrm{e}}{2 \mathrm{~m}}\) (mvr) [∵ Multiplying and dividing with ‘m’ on right side]
∴μ = \(\frac{\mathrm{e}}{2 \mathrm{~m}}\) L where L = mvr = angular momentum.

Qeustion 3.
A bar magnet of length 0.1m and with a magnetic moment of 5Am² is placed in a uniform a magnetic field of intensity 0.4T, with its axis making an angle of 60° with the field. What is the torque on the magnet ?
Answer:
Given, 2l = 0.1m; m = 5A – m²; B = 0.4T; θ = 60°.
Torque, T = mB sin θ = 5 × 0.4 × sin 60° = 2 × \(\frac{\sqrt{3}}{2}\)
∴ T = 1.732 N – m

Question 4.
A solenoid of length 22.5 cm has a total of 900 turns and carries a current of 0.8 A. What is the magnetising field H near the centre and far away from the ends of the solenoid ?
Answer:
l = 22.5 cm = 22.5 × 10^-2 m = \(\frac{45}{2}\) × 10^-2m
N = 900; I = 0.8A; H = ?
H = \(\frac{\mathrm{NI}}{l}=\frac{900 \times 0.8}{\left(\frac{45}{2}\right) \times 10^{-2}}\)
H = \(\frac{900}{45}\) × 0.8 × 10² × 2
∴ H = 3200 Am^-1

Qeustion 5.
The horizontal component of the earth’s magnetic field at a certain place is 2.6 × 10^-5T and the angle of dip is 60°. What is the magnetic field of the earth at this location ?
Answer:
Given H_E = 2.6 × 10^-5T;
D (or) δ = 60°
B_E = \(\frac{\mathrm{H}_{\mathrm{E}}}{\cos \mathrm{D}}=\frac{2.6 \times 10^{-5}}{\cos 60^{\circ}}=\frac{2.6 \times 10^{-5}}{(1 / 2)}\) = 5.2 × 10^-5 T
∴ B_E = 5.2 × 10^-5 T

Question 6.
In the magnetic meridian of a certain place, the horizontal component of the earth’s magnetic field is 0.26 G and the dip angle is 60°. What is the magnetic field of the earth at this location ?
Solution:
It is given that H_E = 0.26 G. From Fig., we have

The earth’s magnetic field, B_E, its horizontal and vertical components. H_E and Z_E. Also shown are the declination, D and the inclination or angle of dip, I.
cos 60° = \(\frac{\mathrm{H}_{\mathrm{E}}}{\mathrm{B}_{\mathrm{E}}}\)
B_E = \(\frac{\mathrm{H}_{\mathrm{E}}}{\cos 60^{\circ}}\)
= \(\frac{0.26}{(1 / 2)}\) = 0.52 G

Qeustion 7.
What is the magnitude of the equatorial and axial fields due to a bar magnet of length 8.0 cm at a distance of 50 cm from its mid-point ? The magnetic moment of the bar magnet is 0.40 A m².
Solution:
From Eq.

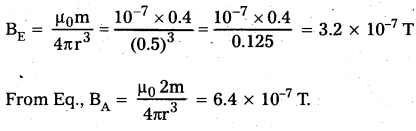
Question 8.
The earth’s magnetic field at the equator is approximately 0.4 G. Estimate the earth’s dipole moment. .
Solution:
The equatorial magnetic field is,
We are given that B_E ~ 0.4 G = 4 × 10^-5 T. For r, we take the radius of the earth 6.4 × 10⁶ m.
Hence,
m = \(\frac{4 \times 10^{-5} \times\left(6.4 \times 10^6\right)^3}{\mu_0 / 4 \pi}\) = 4 × 10² × (6.4 × 10⁶)³ (μ₀/4π = 10^-7)
= 1.05 × 10²³ A m²
This is close to the value 8 × 10²² A m² quoted in geomagnetic texts.

Textual Examples

Question 1.
In Fig, the magnetic needle has magnetic moment 6.7 × 10^-2 Am² and moment of inertia i = 7.5 × 10^-6 kg m². It performs 10 complete oscillations in 6.70 s. What is the magnitude of the magnetic field ?
Solution:
The time period of oscillation is, :
T = \(\frac{6.70}{10}\) = 0.67 s

The axial field of a finite solenoid in order to demonstrate its similarity to that of a bar magnet.
From Eq. B =
= \(\frac{4 \times(3.14)^2 \times 7.5 \times 10^{-6}}{6.7 \times 10^{-2} \times(.067)^2}\)
= 0.01 T

Question 2.
A short bar magnet placed with its axis at 30° with an external field of 800 G experiences a torque of 0.016 Nm.
(a) What is the magnetic moment of the magnet ?
(b) What is the work done in moving it from its most stable to most unstable position ?
(c) The bar magnet is replaced by a solenoid of cross-sectional area 2 × 10^-4 m² and 1000 turns, but of the same magnetic moment. Determine the current flowing through the solenoid.
Solution:
a) From Eq., τ = m B sin θ, θ = 30°, hence sin θ = 1/2.
Thus, 0.016 = m × (800 × 10^-4 T) × (1/2)
m = 160 × 2/800 =0.40 Am²

b) From Eq . U_m = -m. B, the most stable position is θ = 0° and the most unstable position is q = 180°. Work done is given by
W = U_m (θ = 180°) – U_m (θ = 0°)
= 2 m B = 2 × 0.40 × 800 × 10^-4 = 0.064 J

c) From Eq., m_s = NIA. From part (a), m_s = 0.40 Am²
0.40 = 1000 × I × 2 × 10^-4
I = 0.40 × 10⁴/(1000 × 2) = 2A

Question 3.
a) What happens if a bar magnet is cut into two pieces :
(i) transverse to its length,
(ii) along its length ?
b) A magnetised needle in a uniform magnetic field experiences a torque but no net force. An iron nail near a bar magnet, however, experiences a force of attraction in addition to a torque. Why ?
c) Must every magnetic configuration have a north pole and a south pole ? What about the field due to a toroid ?
d) Two identical looking iron bars A and B are given, one of which is definitely known to be magnetised. (We do not know which one.) How would one ascertain whether or not both are magnetised ? If only one is magnetised how does one ascertain which one ? (Use nothing else but the bars A and B].
Solution:
a) In either case, one gets two magnets, each with a north and south pole.

b) No force if the field is uniform. The iron nail experiences a non-uniform field due to the bar magnet. There is induced magnetic moment in the nail, therefore, it experiences both force and torque. Then net force is attractive because the induced south pole (say) in the nail is closer to the north pole of magnet than induced north pole.

c) Not necessarily. True only if the source of the field has a net nonzero magnetic moment. This is not so for a toroid or even for a straight infinite conductor.

d) Try to bring different ends of the bars closer. A repulsive force in some situation establishes that both are magnetised. If it is always attractive, then one of them is not magnetised. In a bar magnet the intensity of the magnetic field is the strongest at the two ends (poles) and weakest at the central region. This fact may be used to determine whether A or B is the magnet. In this case, to see which one of the two bars is magnet, pick up one, (say, A) and lower one of its end first one of the ends of the other (say, B) and then on the middle of B. If you notice that in the middle of B, A experiences no force, then B is magnetised. If you do not notice any change from the end to the middle of B, then A is magnetised.

Question 4.
What is the magnitude of the equatorial and axial fields due to a bar magnet of length 8.0 cm at a distance of 50 cm from its mid-point ? The magnetic moment of the bar magnet is 0.40 A m², the same as in Example – 2.
Solution:
From Eq.

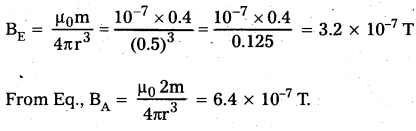
Question 5.
Figure shows a small magnetised needle P placed at a point O. The arrow shows the direction of its magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

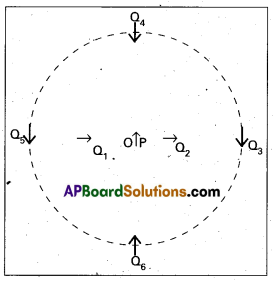
a) In which configuration the system is not in equilibrium ?
b) In which configuration is the system in (i) stable, and (ii) unstable equilibrium ?
c) Which configuration corresponds to the lowest potential energy among all the configurations shown ?
Solution:
Potential energy of the configuration arises due to the potential energy of one dipole (say, Q) in the magnetic field due to other (P). Use the result that the field due to P is given by the expression. *
B_P = –\(\frac{\mu_0}{4 \pi} \frac{\mathrm{m}_{\mathrm{p}}}{\mathrm{r}^3}\) (on the normal bisector)
B_P = \(\frac{\mu_0 2}{4 \pi} \frac{\mathrm{m}_{\mathrm{p}}}{\mathrm{r}^3}\) (on axis)
where mp is the magnetic moment of the dipole P.
Equilibrium is stable when m_Q is parallel to B_P, and unstable when it is anti-parallel to B_P. For instance for the configuration Q₃ for which Q is along the perpendicular bisector of the dipole P, the magnetic moment of Q is parallel to the magnetic field at the position 3. Hence Q₃ is stable. Thus,
a) PQ₁ and PQ₂
b) (i) PQ₃, PQ₆ (stable); (ii) PQ₅, PQ₄ (unstable)
c) PQ₆.

Question 6.
Many of the diagrams given in Fig. show magnetic field lines (thick lines in the figure) wrongly. Point out what is wrong with them. Some of them may describe electrostatic field lines correctly. Point out which ones.

Solution:

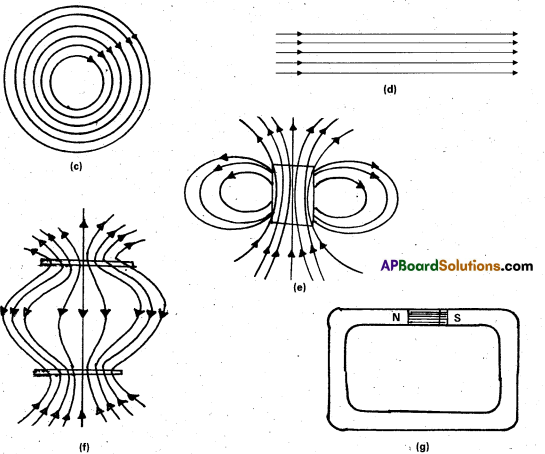
a) Wrong: Magnetic field lines can never emanate from a point, as shown in figure. Over any closed surface, the net flux of B must always be zero, i.e., pictorially as many field lines should seem to enter the surface as the number of lines leaving it. The field lines shown, in fact, represent electric field of a long positively charged wire. The correct magnetic field lines are circling the straight conductor.

b) Wrong: Magnetic field lines (like electric lines) can never cross each other, because otherwise the direction of field at the point of intersection is ambiguous. There is further error in the figure. Magnetostatic field lines can never form closed loops around empty space. A closed loop of static magnetic field line must enclose a region across which a current is passing. By contrast, electrostatic field lines can never form closed loops, neither in empty space, nor when the loop encloses charges.

c) Right: Magnetic lines are completely confined within a toroid: Nothing wrong here in field lines forming closed loops, since each loop encloses a region across which a current passes. Note, for clarity of figure, only a few field lines within the toroid have been shown. Actually, the entire region enclosed by the windings contains magnetic field.,

d) Wrong: Field lines due to a solenoid at its ends and outside cannot be so completely straight and confined; such a thing violates Ampere’s law. The lines should curve out at both ends, and meet eventually to form closed loops.

e) Right: These are field lines outside and inside a bar magnet. Note carefully the direction of field lines inside. Not all field lines emanate out of a north pole (or converge into a south pole). Around both the N-pole, and the S-pole, the next flux of the field is zero.

f) Wrong: These field lines cannot possibly represent a magnetic field. Look at the upper region. All the field lines seem to emanate out of the shaded plate. The net flux through a surface surrounding the shaded plate is not zero. This is impossible for a magnetic field. The given field lines, in fact, show the electrostatic field lines around a positively charged upper plate and a negatively charged lower plate. The difference between Fig. [(e) and (f)] should be carefully grasped.

g) Wrong: Magnetic field lines between two pole pieces cannot be precisely straight at the ends. Some fringing of lines is inevitable. Otherwise, Ampere’s law is violated. This is also true for electric field lines.

Question 7.
a) Magnetic field lines show the direction (at every point) along which a small magnetised needle aligns (at the point). Do the magnetic field line’s also represent the lines of force on a moving charged particle at every point ?
b) Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why ?
c) If magnetic monopoles existed, how would the Gauss’s law of magnetism be modified ?
d) Does a bar magnet exert a torque on itself due to its own field ? Does one element of a current – carrying wire exert a force on another element of the same wire ?
e) Magnetic field arises due to charges in motion. Can a system have magnetic moments even though its net charge is zero ?
Solution:
a) No. The magnetic force is always normal to B (remember magnetic force = qv × B). It is misleading to call magnetic field lines as lines of force.

b) If field lines were entirely confined between two ends of a straight solenoid, the flux through the cross-section at each end would be non-zero. But the flux of field B through any closed surface must always be zero. For a toroid, this difficulty is absent because it has no ‘ends’.

c) Gauss’s law of magnetism states that the flux of,B thrugh any closed surface is always
zero \(\int_s B \cdot d s\) = o.
If monopoles existed, the right hand side would be equal to the monopole (magnetic charge) qm enclosed by S. [Analogous to Gauss’s law of electrostatics, \(\int_s B \cdot d s\) = μ₀q_m
where q_m is the (monopole) magnetic charge enclosed by S.]

d) No. There is no force or torque on an element due to the field produced by that element itself. But there is a force (or torque) on an element of the same wire. (For the special case of a straight wire, this force is zero).

e) Yes. The average of the cahrge in the system may be zero. Yet, the mean of the magnetic moments due to various current loops may not be zero. We will come across such examples in connection with paramagnetic material where atoms have net dipole moment through their net charge is zero.

Question 8.
The earth’s magnetic field at the equator is approximately 0.4 G. Estimate the earth’s dipole moment.
Solution:
The equatorial magnetic field is,
B_E = \(\frac{\mu_0 \mathrm{~m}}{4 \pi \mathrm{r}^3}\)
We are given that B_E ~ 0.4 G = 4 × 10^-5 T. For r, we take the radius of the earth 6.4 × 10⁶ m. Hence,
m = \(\frac{4 \times 10^{-5} \times\left(6.4 \times 10^6\right)^3}{\mu_0 / 4 \pi}\) = 4 × 10² × (6.4 × 10⁶)³ (μ₀/4π = 10^-7)
= 1.05 × 10²³ A m²
This is close to the value 8 × 10²² A m² quoted in geomagnetic texts.

Question 9.
In the magnetic meridian of a certain place, the horizontal component of the earth’s magnetic field is 0.26 G and the dip angle is 60°. What is the magnetic field of the earth at this location ?
Solution:
It is given that H_E = 0.26 G. From Fig., we have

The earth’s magnetic field, B_E, its horizontal and vertical components. H_E and Z_E. Also shown are the declination, D and the inclination or angle of dip, I.
cos 60° = \(\frac{\mathrm{H}_{\mathrm{E}}}{\mathrm{B}_{\mathrm{E}}}\)
B_E = \(\frac{\mathrm{H}_{\mathrm{E}}}{\cos 60^{\circ}}\)
= \(\frac{0.26}{(1 / 2)}\) = 0.52 G

Question 10.
A solenoid has a core of a material with relative permeability 400. The windings of the solenoid are insulated from the core and carry a current of 2A. If the number of turns is 1000 per metre, calculate (a) H, (b) M, (c) B and (d) the magnetising current I_m.
Solution:
a) The field H is dependent of the material of the core, and is
H = nI = 1000 × 2.0 = 2 × 10³ A/m

b) The magnetic field B is given by
B = μ_rμ₀H
= 400 × 4π × 10^-7 (N/A³) × 2 × 10³ (A/m) = 1.0 T

c) Magnetisation is given by
M = (B – μ₀ H)/μ₀
= (μ_rμ₀H – μ₀H)/μ₀ = (μ_r – 1) H = 399 × H ≃ 8 × 10⁵ A/m

d) The magnetising current IM is the additional current that needs to be passed through the windings of the solenoid in the absence of the core which would give a B value as in the presence of the core. Thus B = μ_rn₀ (I + I_M). Using I = 2A, B = 1 T, we get I_M = 794A.

Question 11.
A domain in ferromagnetic iron is in the form of a cube of side length 1 μm. Estimate the number of iron atoms in the domain and the maximum possible dipole moment and magnetisation of the domain. The molecular mass of iron is 55 g/mole and its density is 7.9 g/cm³. Assume that each iron atom has a dipole moment of 9.27 × 10^-24 A m³.
Solution:
The volume of the cubic domain is
V = (10^-6 m)³ = 10^-18 m³ = 10^-12 cm³
Its mass is volume × density = 7.9 g cm^-3 × 10^-12 cm³ = 7.9 × 10^-12 g
It is given that Afagadro number (6.023 × 10²³) of iron atoms have a mass of 55g. Hence,the number of atoms in the domain is
N = \(\frac{7.9 \times 10^{-12} \times 6.023 \times 10^{23}}{55}\)
= 8.65 × 10¹⁰ atoms
The maximum possible dipole moment m_max is achieved for the (unrealistic) case when all the atomic moments are perfectly aligned. Thus,
m_max = (8.65 × 10¹⁰) × (9-27 × 10^-24)
= 8.0 × 10^-13 Am²
The consequent magnetisation is
M_max = m_max/DomainVolume :
= 8.0 × 10^-13 Am²/10^-18 m³
= 8.0 × 10⁵ Am^-1.