Andhra Pradesh BIEAP AP Inter 2nd Year Chemistry Study Material Lesson 3(a) Electro Chemistry Textbook Questions and Answers.
AP Inter 2nd Year Chemistry Study Material Lesson 3(a) Electro Chemistry
Very Short Answer Questions
Question 1.
What is a galvanic cell or a voltaic cell ? Give one example. [T.S. Mar. 19]
Answer:
Galvanic cell: A device which converts chemical energy into electrical energy by the use of spontaneous redox reaction is called Galvanic cell (or) voltaic cell.
Eg.: Daniell cell.
Question 2.
Write the Chemical reaction used in the construction of the Daniell cell together with the half-cell reactions.
Answer:
The chemical reactions used in the construction of the Daniell cell.
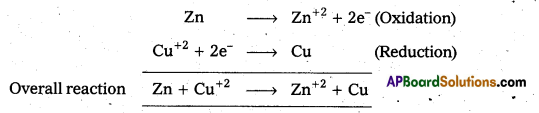
![]()
Question 3.
Name the two half-cell reactions that are taking place in the Daniell cell.
Answer:
The two half cell reactions that are takes place in the Daniell cell are oxidation and reduction.
Zn → Zn+2 + 2e– (Oxidation)
Cu+2 + 2e– → Cu (Reduction)
Question 4.
How is a galvanic cell represented on paper as per IUPAC convention ? Give one example.
Answer:
Representation of a Galvanic cell:
As per IUPAC convention
- Oxidation half cell represented on the left side.
- Reduction half cell represented on the right side.
- Oxidation half cell and reduction half cell are connected by a salt bridge indicated by two vertical parallel lines.
Eg.: Cu(s) | \(\mathrm{Cu}_{(\mathrm{aq})}^{+2}\) || \(\mathrm{Ag}_{(\mathrm{aq})}^{+}\) | Ag(s)
Question 5.
Write the cell reaction taking place in the cell
Cu(s) | \(\mathrm{Cu}_{(\mathrm{aq})}^{+2}\) || \(\mathrm{Ag}_{(\mathrm{aq})}^{+}\) | Ag(s)
Answer:
Given cell is Cu(s) | \(\mathrm{Cu}_{(\mathrm{aq})}^{+2}\) || \(\mathrm{Ag}_{(\mathrm{aq})}^{+}\) | Ag(s)
Cu → Cu+2 + 2e– (Oxidation)
2Ag+ + 2e– → 2Ag (Reduction)
Question 6.
What is standard hydrogen electrode ?
Answer:
The electrode whose potential is known as standard electrode (or) standard hydrogen electrode.
To determine the potential of a single electrode experimentally it combine with standard hydrogen electrode and the EMF of cell so constructed is measured with potentiometer.
![]()
Question 7.
Give a neat sketch of standard hydrogen electrode.
Answer:
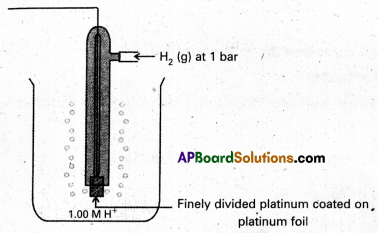
Standard Hydrogen Electrode (SHE)
Question 8.
What is Nernst equation ? Write the equation for an electrode with electrode reaction Mn+(aq) + ne– ⇌ M(s).
Answer:
The electrode potential at any concentration measured with respect to standard hydrogen electrode is represented by Nernst equation.
Nernst equation is
E = E0 + \(\frac{\mathrm{RT}}{\mathrm{nF}}\) ln[Mn+] [Metal Electrodes]
Given electrode reaction is \(\mathrm{M}_{(\mathrm{aq})}^{\mathrm{n}+}\) + ne– ⇌ M(s)
For the above electrode reaction Nemst equation is
E(Mn+/M) = \(\mathrm{E}_{\left(\mathrm{M}^{\mathrm{n}+} / \mathrm{M}\right)}^0+\frac{\mathrm{RT}}{\mathrm{nF}} \ln \left[\mathrm{M}^{\mathrm{n}+}\right]\)
Here E(Mn+/M) = Electrode potential
E0E(Mn+/M) = Standard Electrode potential
R = gas constant = 8.314 J/k.mole
F = Faraday = 96487 c/mole
T = temperature
[Mn+] = concentration of species Mn+
Question 9.
A negative E0 indicates that the redox couple is _______________ reducing couple than H+/H2, couple, (powerful or weak)
Answer:
A negative E0 value indicates that the redox couple is powerful reducing couple than H+/H2 couple.
Question 10.
A positive E0 indicates that the redox couple is a weaker _____________ couple than H+/H2 couple. (oxidising or reducing)
Answer:
A positive E0 value indicates that the redox couple is as weaker reducing couple than H+/H2 couple.
![]()
Question 11.
Write the Nernst equation for the EMF of the cell .
Ni(s) |\(\mathrm{Ni}_{(\mathrm{aq})}^{2+}\) || \(\mathrm{Ag}_{(\mathrm{aq})}^{+}\) | Ag
Answer:
Given cell is Ni(s) |\(\mathrm{Ni}_{(\mathrm{aq})}^{2+}\) || \(\mathrm{Ag}_{(\mathrm{aq})}^{+}\) | Ag
Nernst equation for the cell is
Ecell = \(\mathrm{E}_{\text {cell }}^0+\frac{\mathrm{RT}}{\mathrm{nF}} \ln \frac{\left[\mathrm{Ag}^{+}\right]}{[\mathrm{Ni}]^{+2}}\)
Question 12.
Write the cell reaction for which Ecell = \(\mathrm{E}_{\text {cell }}^0-\frac{\mathrm{RT}}{2 \mathrm{~F}} \ln \frac{\left[\mathrm{Mg}^{2+}\right]}{\left[\mathrm{Ag}^{+}\right]^2}\)
Answer:
Given Ecell = \(\mathrm{E}_{\text {cell }}^0-\frac{\mathrm{RT}}{2 \mathrm{~F}} \ln \frac{\left[\mathrm{Mg}^{2+}\right]}{\left[\mathrm{Ag}^{+}\right]^2}\)
The cell reaction is Mg(s)/\(\mathrm{Mg}_{(\mathrm{aq})}^{2+}\) || \(\mathrm{Ag}_{(\mathrm{aq})}^{+}\) | Ag(s)
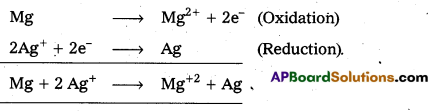
Question 13.
How is E0 cell related mathematically to the equilibrium constant Kc of the cell reaction?
Answer:
Relation between E0 cell and equilibrium constant KC of the cell reaction
\(\mathrm{E}_{\text {cell }}^0=\frac{2.303 \mathrm{RT}}{\mathrm{nF}}\) log KC
n = number of electrons involved
F = Faraday 96500 C mol-1,
T = Temperature
R = gas constant
Question 14.
How is Gibbs energy (G) related to the cell emf (E) mathematically ?
Answer:
Relation between Gibb’s energy (G) and emf (E) mathematically
∆G0 = -nFE(cell)
∆G = change in Gibb’s energy
n = number of electrons involved
F = Faraday = 96500 C mol-1
Question 15.
Define conductivity of a material. Give its SI units.
Answer:
The reciprocal of specific resistance (or) resistivity is called conductivity.
It is represented by (κ)
(Or)
The conductance of one unit cube of a conductor is also called conductivity.
SI units : ohm-1 m-1 (or) Sm-1 S = Siemen
![]()
Question 16.
What is cell constant of a conductivity cell ?
Answer:
Resistance R = ρ . \(\frac{l}{\mathrm{~A}}\) = \(\frac{l}{\kappa \cdot \mathrm{A}}\)
\(\frac{l}{\mathrm{~A}}\) = cell constant
Cell constant G = \(\frac{l}{\mathrm{~A}}\) = R × κ
The cell constant of a conductivity cell is the product of resistance and specific conductance.
Question 17.
Define molar conductivity ∧m and how is it related to conductivity (κ) ?
Answer:
Molar conductivity: The conductivity of a volume of solution containing one gram molecular weight of the electrolyte placed between two parallel electrodes separated by a distance of unit length of 1 meter is called molar conductivity (∧m).
Relation between conductivity and molar conductivity:
∧m = \(\frac{\kappa}{\mathrm{c}}\);
∴ c = constant
Question 18.
Give the mathematical equation which gives the variation of molar conductivity with ∧m the molarity (c) of the solution ?
Answer:
The mathematical equation which gives the variation of molar conductivity ∧m with the molarity (c) of the solution is
∧m = \(\frac{\kappa}{1000\left(\text { lit } / \mathrm{cm}^3\right) \times \text { molarity (moles/lit) }}=\frac{\kappa \times 1000\left(\mathrm{~cm}^3 / \mathrm{lit}\right)}{\text { molarity (mole/lit) }}\)
Question 19.
State Kohlrausch’s law of independent migration of ions.
Answer:
Kohlrausch’s law of independent migration of ions: The limiting molar conductivity of an electrolytes can be represented as the sum of the individual contributions of the anion and the cation of the electrolytes.
\(\lambda_{\mathrm{m}(\mathrm{AB})}^0=\lambda_{\mathrm{A}^{+}}^0+\lambda_{\mathrm{B}^{-}}^0\)
\(\lambda_m^0\) = Limiting molar conductivity
\(\lambda_A^0\) = Limiting molar conductivity of cation
\(\lambda_B^0\) = Limiting molar conductivity of anion
Question 20.
State Faraday’s first law of electrolysis. [A.P. Mar. 18, 16] [Mar. 14]
Answer:
The amount of chemical reaction which occurs at any electrode during electrolysis is proportional to the quantity of current passing through the electrolyte.
(Or)
The mass of the substance deposited at an electrode during the electrolysis of electrolyte is directly proportional to quantity of electricity passed through it.
m ∝ Q; m ∝ c × t
m = ect; m = \(\frac{\text { Ect }}{96,500}\)
e = electrochemical equivalent
c = Current in amperes
t = time in seconds
E = Chemical equivalent
![]()
Question 21.
State Faraday’s second law of electrolysis. [T.S. Mar. 18] [Mar. 14]
Answer:
The amounts of different substances liberated when the same quantity of electricity is passed through the electrolytic solution are proportional to their chemical equivalent weights.
m ∝ E
Qustion 22.
What are the products obtained at the platinum anode and the platinum cathode respectively in the electrolysis of fused or molten NaCl ?
Answer:
In the electrolysis of fused (or) molten NaCl with platinum anode and platinum cathode, sodium metal obtained at cathode and chlorine gas at anode
2 NaCl → 2 Na+ + 2Cl–
2 Cl– → Cl2 + 2e– (anode)
2 Na+ + 2e– → 2 Na (cathode)
Question 23.
Give the products obtained at the platinum electrodes (cathode and anode) when aqueous solution of K2SO4 is electrolysed.
Answer:
During the electrolysis of aq.K2SO4 using pt-anode and pt-cathode hydrogen gas liberated at cathode and oxygen gas at anode.
K2SO4 → 2K+ + \(\mathrm{SO}_4^{-2}\)
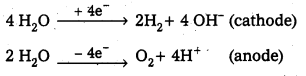
Question 24.
Write the chemical equation corresponding to the oxidation of H2O(l) at the platinum anode.
Answer:
The chemical equation corresponding to the oxidation of H2O(l) at the platinum anode is
2H2O(l) → O2(g) + 4H+(aq) + 4e–
![]()
Question 25.
Give the chemical equation that represents the reduction of liquid water H2O(l)at the platinum cathode.
Answer:
The chemical equation that represents the reduction of liquid water H2O(l) at the platinum cathode is H2O(l) + e– → \(\frac{1}{2}\)H2(g) + OH–
Question 26.
What is a primary battery ? Give one example. [A.P. Mar. 17]
Answer:
The batteries which after their use over a period of time, becomes dead and the cell reaction is completed and this cannot be reused again are called primary batteries.
Eg: Leclanche cell, dry cell.
Question 27.
Give one example for a secondary battery. Give the cell reaction.
Answer:
Lead storage battery is an example of secondary battery.
The cell reactions when the battery is in use are
Pb(s) + \(\mathrm{SO}_4^{-2} \text { (aq) }\) → PbSO4(s) + 2e– (Anode)
PbO2(s) + \(\mathrm{SO}_4^{-2} \text { (aq) }\) → \(4 \mathrm{H}_{(\mathrm{aq})}^{+}\) + 2e– → PbSO4(s) + 2 H2O(l) (Cathode)
Overall cell reaction is .
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(s) + H2O(l)
Question 28.
Give the cell reaction of nickel-cadmium secondary battery.
Answer:
The cell reaction of nickel-cadmium secondary battery is
Cd(s) + 2Ni(OH)3(s) → CdO(s) + 2 Ni(OH)2(s) + H2O(l)
Question 29.
What is a fuel cell ? How is it different from a conventional galvanic cell ?
Answer:
A fuel cell is a galvanic cell in which the chemical energy of fuel-oxidant system is converted directly into electrical energy.
- Conventional Galvanic cell converts chemical energy into electrical energy by spontaneous redox reactions.
- Fuel cell convert energy of combustion of fuels like hydrogen, methane etc., into electrical energy. These cause less pollution.
Question 30.
Give the electrode reactions occurijig at the anode and at the cathode in H2, O2, fuel cell.
Answer:
At cathode : O2(g) + 2 H2, O2 + 4e– → 4OH–(aq)
At anode : 2H2(g) + 4 OH–(aq) → 4H2O(l) + 4e–
Overall reaction : 2H2(g) + O2(g) → 2H2O(l)
![]()
Question 31.
What is metallic corrosion ? Give one example. [T.S. Mar. 17; A.P. Mar. 15]
Answer:
Metallic corrosion: The natural tendency of conversion of a metal into its mineral compound form i n interaction with the environment is known as metallic corrosion.
Eg : 1) Iron converts itself into its oxide [Rusting] (Fe2O3)
2) Silver converts itself into it’s sulphate
[tarnishing] [Ag2S]
Question 32.
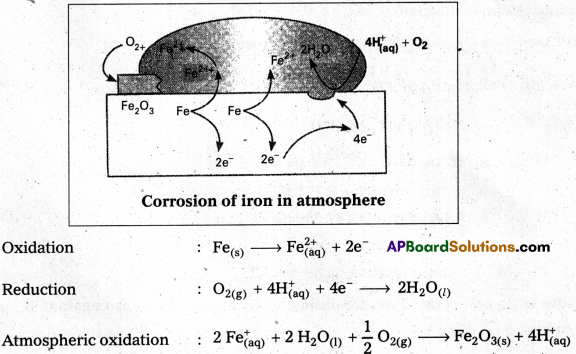
Give the electro-chemical reaction that represents the corrosion or rusting of iron.
Answer:
Rusting of iron: Iron converts itself into its oxixe Fe2O3
The electrochemical reaction that represents the corrosion or rusting of iron is
Anode : 2 Fe(s) → 2 Fe2+ + 4e– \(\mathrm{E}_{\left(\mathrm{Fe}^{2+} / \mathrm{Fe}\right)}^0\) = -0.44V
Cathode : O2(g) + 4H+(aq) + 4e– → 2H2O(l) \(\mathrm{E}_{\mathrm{H}^{+} / \mathrm{O}_2 / \mathrm{H}_2 \mathrm{O}}^{\Theta}\) = 1.23V
Overall reaction: 2 Fe(s) + O2(g) + 4H+(aq) → 2Fe+2aq + 2 H2O(l) \(\mathrm{E}_{\text {(cell) }}^{\Theta}\) = 1.67 V
Short Answer Questions
Question 1.
What are galvanic cells ? Explain the working of a galvanic cell with a neat sketch taking Daniell cell as example. [T.S. & A.P. Mar. 18]
Answer:
Galvanic cell: A device which converts chemical energy into electrical energy by the use of spontaneous redox reaction is called Galvanic cell (or) voltaic cell.
Eg : Daniell cell.
Daniell cell: It is a special type of galvanic cell. It contains two half cells in the same vessel. The vessel is devided into two chambers. Left chamber is filled with ZnSO4 (aq) solution and Zn – rod is dipped into it. Right chamber is filled with aq. CuSO4 solution and a copper rod is dipped into it. Process diaphragm acts as Salt bridge. The two half cell’s are connected to external battery.
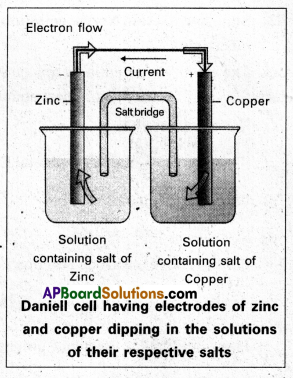
Cell reactions :
Ion Zn/ZnSO4 half cell, oxidation, reaction occurs
Zn → Zn2+ + 2e–
Ion Cu/CuSO4 half cell, reduction reaction occurs.
The net cell reaction is
Zn + Cu+2 ⇌ Zn+2 + Cu
Cell is represented as Zn / Zn+2 || Cu+2 / Cu
![]()
Question 2.
Give the construction and working of a standard hydrogen electrode with a neat diagram.
Answer:
To determine the potential of a single electrode experimentally, it is combined with a standard hydrogen electrode (electrode whose potential is known) and the EMF of the cell. So constructed is measured with a potentiometer. Standard hydrogen electrode is constructed and is used as standard electrode or reference electrode. Standard Hydrogen Electrode (SHE) or Normal Hydrogen Electrode (NHE).
Pure hydrogen gas is bubbled into a solution of 1M HCl along a platinum electrode coated with platinum block. A platinum block electrode placed in the solution at atmospheric pressure.
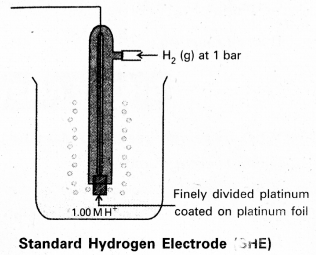
Generally the electrode is fitted into the tube. The tube will have two circular small holes. This tube is immersed in the acid solution such that one haf of the circular hole is exposed to air and another half in the solution.
The following equilibrium exists at the electrode.
\(\frac{1}{2}\) H2(g) (1atm) ⇌ \(\mathrm{H}_{(\mathrm{aq})}^{+}\) (1M) + e–
Question 3.
State and explain Nernst equation with the help of a metallic electrode and a non-metallic electrode.
Answer:
The electrode potential at any concentration measured with respect to standard hydrogen electro represented by Nernst equation.
Nernstst equation is
E = E0 + \(\frac{\mathrm{RT}}{\mathrm{nF}}\) In [Mn+] [Metal Electrodes]
Given electrode reaction is
\(\mathrm{M}_{(\mathrm{aq})}^{\mathrm{n}+}\) + ne– ⇌ M(s)
For the above electrode reaction Nernst equation is
E(Mn+ / M) = \(\mathrm{E}_{\left(\mathrm{M}^{\mathrm{n}+} / \mathrm{M}\right)}^0+\frac{\mathrm{RT}}{\mathrm{nF}} \ln \left[\mathrm{M}^{\mathrm{n}+}\right]\)
Here E(Mn+ / M) = Electrode potential
E0(Mn+ / M) = Standard Electrode potential
R = gas constant = 8.314 J/k.mole
F = Faraday = 96487 c/mole
T = temperature
[Mn+] = concentration of species Mn+
For non-metal electrodes :
E = E0 – \(\frac{\mathrm{RT}}{\mathrm{nF}}\) ln C ; C = concentration
Example for metal electrode:
Given cell is Ni(s) | \(\mathrm{Ni}_{(a q)}^{2+}\) || \(\) | Ag
Nernst equation for the cell is
Ecell = \(\mathrm{E}_{\text {cell }}^0+\frac{\mathrm{RT}}{\mathrm{nF}} \ln \frac{\left[\mathrm{Ag}^{+}\right]}{[\mathrm{Ni}]^{+2}}\)
Example for non-metal electrode: Pt, Cl2/Cl–
E = E0 – \(\frac{\mathrm{RT}}{\mathrm{nF}}\) log C
E = E0 – \(\frac{\mathrm{RT}}{\mathrm{F}}\) log C
![]()
Question 4.
Explain with a suitable example the relation between the Gibbs energy of chemical reaction (G) and the functioning of the electrochemical cell.
Answer:
Electrical work done in one second in an electrochemical cell is equal to the electrical potential multiplied by the total charge passing. If we want to obtain maximum work from a galvanic cell then the charge has to be passed reversibly. The reversible work done by a galvanic cell is equal to decrease in its Gibbs energy and therefore, if the emf is E and nF is the amount of charge passing and ∆rG = – nFE[cell]
It may be remembered that E[cell] is an intensive parameter but ∆rG is an extensive thermodynamic property and the value depends on n. Thus, if we write the reaction
Zn[s] + \(\mathrm{Cu}_{[\mathrm{aq}]}^{2+}\) → \(\mathrm{Zn}_{\text {[aq] }}^{2+}\) + Cu[s]
∆rG = -2FE[cell]
but when we write the reaction
2 Zn[S] + 2 \(\mathrm{Cu}_{[\mathrm{aq}]}^{2+}\) → \(\mathrm{Zn}_{[\text {aq] }}^{2+}\) + 2 Cu[s]
∆rG = -4FE[cell]
If the concentration of each of the reacting species is unity, then E[cell] = \(\mathrm{E}_{\text {[cell] }}^{\Theta}\) and we have
∆rG⊖ -nF\(\mathrm{E}_{\text {[cell] }}^{\Theta}\)
We can calculate equilibrium constant using the equation
∆rG⊖ = – RTln Kc
Question 5.
On what factors the electrical conductance of an aqueous solution of electrolyte depends?
Answer:
The electrical conductance of an aqueous solution of electrolyte depends on
- The nature of the electrolyte
- Size and solvation of the ions formed in the dissociation of the electrolyte.
- The nature and viscosity of the solvent.
- Concentration of the electrolyte
- Temperature
Question 6.
How is molar conductivity of an aqueous electrolyte solution measured experimentally ?
Answer:
Molar conductivity: The conductivity of a volume of solution containing one gram molecular weight of the electrolyte placed between two parallel electrodes separated by a distance of unit length of 1 meter is called molar conductivity (∧m)
Relation between conductivity and molar conductivity:
∧m = \(\frac{\kappa}{\mathrm{c}}\);
∴ c = constant .
The conductance of a solution measured in a conductivity cell.
By using the conductivity cells
Resistance (R) = \(\frac{l}{\kappa \times A}\)
l = distance between electrodes; A = Area of cross section; K = conductivity
G* = \(\frac{l}{\mathrm{~A}}\) = cell constant
-4 Cell constant is measured by measuring the resistance of the cell containing a solution whose conductivity is known.
-4 Cell constant determined is used for measuring the resistance (or) conductivity.
∴ molar conductivity ∧(m) = \(\frac{\kappa}{\mathrm{c}}\)
∧(m) = \(\frac{\kappa\left(\mathrm{Scm}^{-1}\right)}{1000\left(\mathrm{~L}^{-3}\right) \text { molarity (moles/lit) }}\)
Question 7.
Explain the variation of molar conductivity with the change in the concentration of the electrolyte. Give reasons.
Answer:
Molar conductivity of a solution at a given concentration is the conductance of the volume of solution containing one mole of electrolyte kept between two electrodes with area of cross section A and distance of unit length.
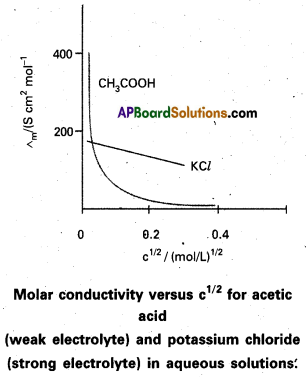
Molar conductivity ∧m = \(\frac{\mathrm{\kappa A}}{l}\)
∧m = κ × V (∵ l = 1, A = V)
V = Volume containing 1 mole of electrolyte
Molar conductivity increase with decrease in concentration of electrolyte (or) increase in dilution. This is due to total volume V of solution containing one mole of electrolyte also increases.
When concentration approaches to zero, the molar conductivity is known as limiting molar conductivity and it is represented by
For strong electrolytes molar conductivity is given by \(\wedge_m^0\)
∧m = \(\wedge_m^0\) – Ac1/2
For weak electrolytes limiting’ molar conductivity is given by
λAB+ = λA+ + λB– (Kohlrausch law)
![]()
Question 8.
State and explain Kohlrausch’s law of independent migration of ions. [T.S. Mar. 16; A.P. Mar. 15]
Answer:
Kohlrausch’s law of independent migration of ions: The limiting molar conductivity of an electrolytes can be represented as the sum of the individual contributions of the anion and the cation of the electrolytes.
\(\lambda_{\mathrm{m}(\mathrm{AB})}^0=\lambda_{\mathrm{A}^{+}}^0+\lambda_{\mathrm{B}^{-}}^0\)
\(\lambda_{\mathrm{m}}^0\) = Limiting molar conductivity
\(\lambda_{\mathrm{A}^{+}}^0\) = Limiting molar conductivity of cation
\(\lambda_{\mathrm{B}^{-}}^0\) = Limiting molar conductivity of anion
Applications:
- Kohlrausch’s law is used in the calculation of the limiting molar conductivity of weak electrolytes.
Eg : λCH3COOH = λCH3COONa + λHCl – λNaCl
= λCH3COO– + λNa+ + λH+ - This law is used in the calculation of degree of dissociation of a weak electrolyte.
- This law is used in the calculation of solubility of sparingly soluble salts like AgCl, BaSO4 etc.
Question 9.
What is electrolysis ? Give Faraday’s first law of electrolysis. [A.P. & T.S. Mar. 15]
Answer:
Electrolysis : The decomposition of a chemical compound in the molten state or in the solution state into its constituent elements under the influence of an applied EMF is called electrolysis.
The amount of chemical reaction which occurs at any electrode during electrolysis is proportional to the quantity of current passing through the electrolyte.
(Or)
The mass of the substance deposited at an electrode during the electrolysis of electrolyte is directly proportional to quantity of electricity passed through it.
m ∝ Q; m ∝ c × t
m = ect; m = \(\frac{\text { Ect }}{96,500}\)
e = electrochemical equivalent
t = time in seconds
c = Current in amperes
E = Chemical equivalent
Question 10.
What are the products obtained at the cathode and anode during the electrolysis of the following when platinum electrodes are used in the electrolysis
a) Molten KCl
b) Aq. CuSO4 solution
c) Aq. K2SO4 solution
Answer:
a) During the electrolysis of molten KCl using platinum electrodes. Potassium is obtained at cathode and chlorine at anode.
2 KCl → 2K+ + 2Cl–
2 Cl– → Cl2 + 2e– (anode)
2K+ + 2e– → 2K (cathode)
b) During the electrolysis of aq.CuS04 solution using platinum electrodes, O2 gas liberated at anode and Cu deposited at cathode.
2 CuSO4 → 2 Cu+2 + 2 SO-24
2 Cu+2 + 4e– → 2 Cu (cathode)
2H2O – 4e– → O2 + 4H+ (anode)
c) During the electrolysis of aq.k2SO4 using pt-anode and pt-cathode hydrogen gas liberated at cathode and oxygen gas at anode.
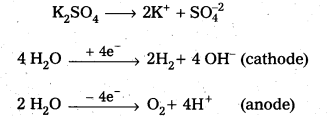
![]()
Question 11.
What are primary and secondary batteries ? Give one example for each.
Answer:
The batteries which after their use over a period of time’ becomes dead and the cell reaction is completed and this cannot be reused again are called primary batteries.
Eg : Leclanche cell, dry cell.
Secondary battery: A secondary battery is the battery in which after it’s use can be recharged and can be used again.
A good secondary battery undergoes large no. of discharging and charging cycles.
Lead storage battery is an example of secondary battery. ,
The cell reactions when the battery is in use are
Pb(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → PbSO4(s) + 2e– (Anode)
PbO2(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → \(4 \mathrm{H}_{\text {(aq) }}^{+}\) + 2e → PbSO4(s) + 2 H2O(l) (Cathode)
Overall cell reaction is
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(aq) + 2H2O(l)
Question 12.
What are the fuel cells ? How are they different from galvanic cells ? Give the construction of H2, O2 fuel cell? [T.S. Mar. 17]
Answer:
A fuel cell is a galvanic cell in which the chemical energy of fuel-oxidant system is converted directly into electrical energy.
- Conventional Galvanic cell converts chemical energy into electrical energy by spontaneous redox reactions.
- Fuel cell convert energy of combustion of fuels like hydrogen, methane etc., into electrical energy. These cause less pollution.
H2 – O2 fuel cell: In this cell, hydrogen and oxygen are bubbled through porous carbon electrodes into Cone. NaOH solution. Electrodes are embedded with suitable catalysts. The electrode reactions are:
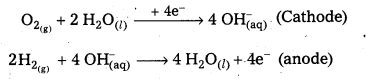
Overall reaction : 2H2(g) + O2(g) → 2 H2O(l)
The cell functions as long as the reacting gases are in supply. The heat of combustion is directly converted into electrical energy.
Question 13.
What is metallic corrosion ? Explain it with respect to iron corrosion.
Answer:
Metallic corrosion: The natural tendency of conversion of a metal into its mineral compound form on interaction with the environment is known as metallic corrosion.
Eg.: 1) Iron converts itself into its oxide [Rusting] (Fe2O3)
2) Silver converts itself into it’s sulphate [tarnishing] [Ag2S]
Rusting of iron : Iron converts it self into its oxixe Fe2O3
The electrochemical reaction that represents the corrosion or rusting-of iron is
Anode : 2 Fe(s) → 2 Fe2+ + 4e– \(\mathrm{E}_{\left(\mathrm{Fe}^{2+} / \mathrm{Fe}\right)}^0\) = -0.44 V
Cathode : O2(g) + \(4 \mathrm{H}_{\text {(aq) }}^{+}\) + 4e– → 22O(l) \(\) = 1.23 V
Overall reaction : 2 Fe(s) + O2(g) + \(4 \mathrm{H}_{\text {(aq) }}^{+}\) → \(2 \mathrm{Fe}_{\mathrm{aq}}^{+2}\) + 2 H2O(l) \(\mathrm{E}_{(\text {cell) }}^{\Theta}\) = 1.67 V
Long Answer Questions
Question 1.
What are electro chemical cells ? How are they constructed ? Explain the working of the different types of galvanic cells ?
Answer:
Electrochemical cell is a device which makes use of a spontaneous redox reaction for the generation of electrical energy.
Eg : Galvanic cell, Daniell cell etc.
Galvanic cell: A device which converts chemical energy into electrical energy by the use of spontaneous redox reaction is called Galvanic cell (or) voltaic cell.
Eg : Daniell cell.
Daniell cell: It is a special type of galvanic cell. It contains two half cells in the same vessel.
The vessel is devided into two chambers. Left chamber is filled with ZnSO4 (aq) solution and Zn – rod is dipped into it, Right chamber is filled with aq. CuSO4 solution and a copper rod is dipped into it. Process diaphragm acts as Salt bridge. The two half cell’s are connected to external battery.
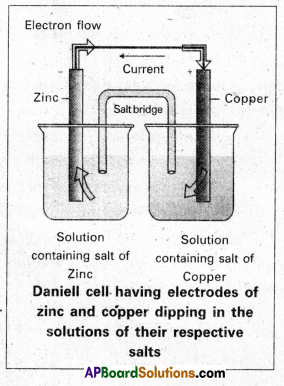
Cell reactions :
Ion Zn/ZnSO4 half cell, oxidation, reaction occurs
Zn → Zn2+ + 2e–
Ion Cu/CuSO4 half cell, reduction reaction occurs.
Cu+2 + 2e– → Cu
The net cell reaction is
Zn + Cu+2 ⇌ Zn+2 + Cu
Cell is represented as Zn / Zn+2 // Cu2+ / Cu
- The two vertical lines (||) represents a salt bridge.
- It is U shaped tube filled with KCl and agar agar gel salt bridge maintains the electrical neutrality and flow of current.
The batteries which after their use over a period of time, becomes dead and the cell reaction is completed and this cannot be reused again are called primary batteries.
Eg : Leclanche cell, dry cell.
Secondary battery: A secondary battery is the battery in which after it’s use can be recharged and can be used again.
A good secondary battery undergoes large no. of discharging and charging cycles.
Lead storage battery is an example of secondaiy battery.
The cell reactions when the battery is in use are
Pb(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → PbSO4(s) + 2e– (Anode)
PbO2(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → \(4 \mathrm{H}_{\text {(aq) }}^{+}\) + 2e → PbSO4(s) + 2 H2O(l) (Cathode)
Overall cell reaction is
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(aq) + 2H2O(l)
In batteries also the principle involved same as in the galvanic cell.
![]()
Question 2.
What is electrical conductace of a solution? How ¡s it measured experimentally?
Answer:
The reciprocal of resistance (R) is known as conductance (c)
\(\frac{l}{\mathrm{R}}=\kappa \times \frac{1}{l / \mathrm{A}}\)
c = \(\kappa \times \frac{1}{l / \mathrm{A}}\)
The conductance or the current conducting capacity of an electrolytic solution can be expressed as .
- Specific conductance (κ),
- Molar conductivity (∧m)
1. Specific conductance : The conductance of the solution enclosed between two parallel electrodes of unit area of cross section separated by unit distance is called specific conductance (κ).
2. Molar conductivity (∧m) : The conductivity of a volume of solution containing one gram molecular weight of the electrolyte placed between two parallel electrodes separated by a distance of unit length of 1 meter is called molar conductivity (∧m)
Relation between conductivity and molar conductivity :
∧m = \(\frac{\kappa}{\mathrm{c}}\); ∴ c = constant
Measurement of electrical conductance :
- The resistance of a metallic wire can be measured with a Wheatstone bridge.
- In measuring the resistance of an electrolytic solution two problems are identified.
- On passing direct current (DC) through the solution changes the composition of the solution due to electrolysis.
- A solution cannot be connected to the measuring bridge like a metallic wire.
- First problem solved by using AC instead of DC. .
- Second problem solved by using specially designed vessel called conductivity cell.
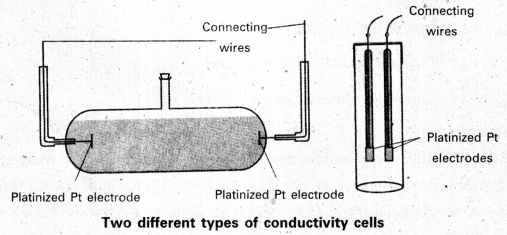
By using above cells,
Resistance R = \(\frac{l}{\kappa \times \mathrm{A}}\)
l = distance between electrodes; A = Area of cross section; κ = conductivity
\(\frac{l}{\mathrm{~A}}\) = cell constant = G*
∴ G* = \(\frac{l}{\mathrm{~A}}\) = R × κ
The cell constant (G*) is determined by measuring the resistance of the cell containing a solution whose conductivity is already known - Cell constant once determined, used for measuring the resistance (or) conductivity.
- The set up for the measurement of the resistance is shown in following figure.
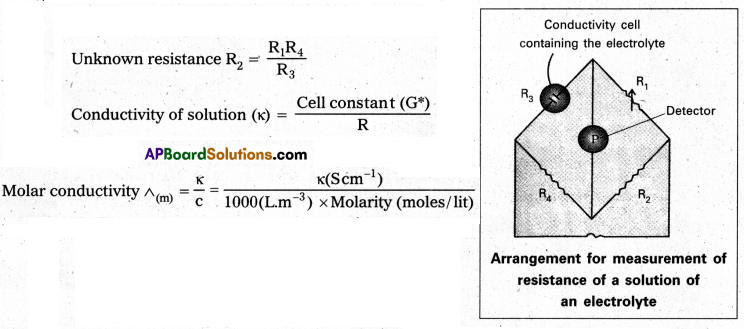
Question 3.
Give the applications of Kohlrausch’s law of independent migration of ions. [T.S. Mar. 16]
Answer:
Kohlrausch’s law of independent migration of ions: The limiting molar conductivity of an electrolytes can be represented as the sum of the individual contributions of the anion and the cation of the electrolytes.
\(\lambda_{\mathrm{m}(\mathrm{AB})}^0=\lambda_{\mathrm{A}^{+}}^0+\lambda_{\mathrm{B}^{-}}^0\)
\(\lambda_{\mathrm{m}}^0\) = Limiting molar conductivity
\(\lambda_{\mathrm{A}^{+}}^0\) = Limiting molar conductivity of cation
\(\lambda_{\mathrm{B}^{-}}^0\) = Limiting molar conductivity of anion
Applications:
1) Calculation of limiting molar conductance at infinite dilution (∧∞) of weak electrolytes :
Limiting molar conductance of weak electrolytes at infinite dilution- cannot be obtained graphically by extrapolation method. However the application of Kohlrausch’s law enables indirect evaluations in such cases.
Eg: Limiting molar conductance of acetic acid at infinite dilution can be calculated from the limiting molar conductances at infinite dilution of hydrochloric acid, sodium chloride and sodium acetate, as illustrated below:
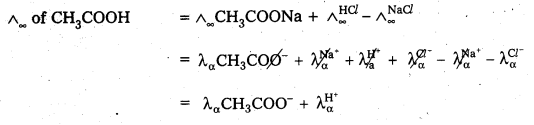
2) Calculation of degree of dissociation of a weak electrolyte :
Degree of dissociation (α) = \(\frac{\lambda_{\mathrm{v}}}{\lambda_{\infty}}\)
Where λv = Limiting molar conductivity at a given concentration or dilution.
λ∞ = Limiting molar conductivity of given electrolyte at infinite dilution.
3) Calculation of the solubility (s) of sparingly soluble salts like AgCl, BaSO4 etc.
S = \(\frac{\kappa \times 1000}{\wedge_{\infty}}\)
where K = specific conductance
∧∞ = Limiting molar conductance at infinite dilution.
![]()
Question 4.
Give the different types of batteries and explain the construction and working of each type of battery. [A.P. Mar. 19]
Answer:
The batteries which after their use over a period of time, becomes dead and the cell reaction is completed and this cannot be reused again are called primary batteries.
Eg.: Leclanche cell, dry cell.
Secondary battery:
A secondary battery is the battery in which after it’s use can be recharged and can be used again.
A good secondary battery undergoes large no. of discharging and charging cycles.
Lead storage battery is an example of secondary battery.
The cell reactions when the battery is in use are
Pb(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → PbSO4(s) + 2e– (Anode)
PbO2(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → \(4 \mathrm{H}_{\text {(aq) }}^{+}\) + 2e → PbSO4(s) + 2 H2O(l) (Cathode)
Overall cell reaction is
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(aq) + 2H2O(l)
Construction and working of primary batteries :
Dry cell:
- This is a modification of Leclanche cell. The liquid state electrolytes (in Leclanche cell) are replaced by paste electrolytes.
- A cylindrical ‘Zn’ vessel is covered with a cardboard. This is sealed with pitch. Zn vessel acts as negative electrode. A carbon rod is introduced at the centre of the Zn vessel. This carbon rod acts as positive electrode.
- Carbon rod is surrounded by a paste of (C + MnO2). The remaining space is filled with (NH4Cl + ZnCl2 paste. The two pastes are separated by a porous sheet.
- These cells are easy to handle and used in radios, watches, torch lights etc. The cell potential is approximately 1.5 V
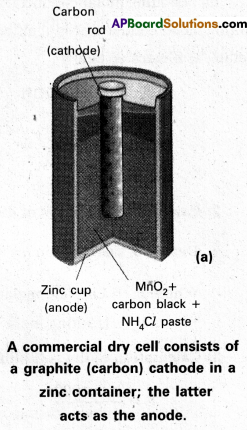
- Electrode reactions:
Cathode : MnO2 + \(\mathrm{NH}_4^{+}\) + eΘ → MnO (OH) + NH3
Anode : Zn + 2MnO2 + 2H2O → Zn2+ + 2OHΘ + 2MnO (OH)
Some of the secondary reactions are
2 NH4Cl + 2OHΘ → 2NH3 + 2Cl– + 2H2O
Zn2+ + 2NH3 + 2Cl– → [Zn (NH3)2] Cl2
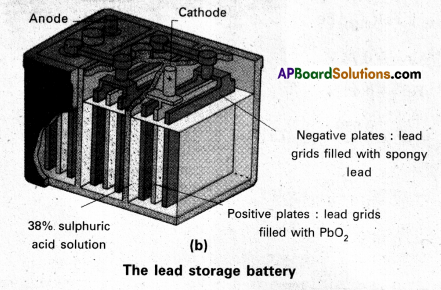
Secondary batteries – construction and working : A secondary cell after its use can be recharged and can be used again. A good secondary cell undergoes a large number of discharging and charging cycles. The most important secondary cell in use is the lead storage battery (fig.(b)). This is commonly used in automobiles and invertors. It consists of a lead anode and a grid of lead packed with lead dioxide (PbO2) as cathode. A 38% solution of sulphuric acid is used as electrolyte.
The cell reactions when the battery is in use (discharging) are :
Anode : Pb(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → PbSO4(s) + 2e–
Cathode: PbO2(s) + \(\mathrm{SO}_4^{-2}(\mathrm{aq})\) → \(4 \mathrm{H}_{\text {(aq) }}^{+}\) + 2e → PbSO4(s) + 2 H2O(l)
i.e., overall cell reaction consisting of cathode and anode reactions is
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(aq) + 2H2O(l)
These reactions occur during discharge i.e., during use of the battery.
On charging the discharged battery the above reaction is reversed and PbSO4 (s) on anode and cathode is converted into Pb and PbO2, respectively.
Problems
Question 1.
The standard potentials of some electrodes are as follows. Arrange the metals in an increasing order of their reducing power.
1) K+/K = -2.93 V
2) Ag+/Ag = 0.8OEV
3) Cu2+/Cu = 0.34 V
4) Mg2+/Mg = -2.37 V
5) Cr3+/Cr = – 0.74V
6) Fe2+/Fe = —0.44 V
Solution:
Given
E0 of cells K+/K = —2.93
Mg+2/Mg = -2.37 V
Ag+/Ag = 0.80 V
Cr+3/Cr = -0.74 V
Cu+2/Cu = 0.34 V
Fe+2/Fe = -0.44 V
Lower the reduction potential values indicates high reducing power and high value indicates the high oxidising power.
So, increasing order of the given cells reducing power is
Ag < Cu < Fe < Cr < Mg < K.
![]()
Question 2.
Calculate the emf of the cell at 25°C
Cr | Cr3+ (0.1 M) || Fe2+ (0.01M) | Fe, given that \(\mathrm{E}_{\mathrm{Cr}^{3+} / \mathrm{Cr}}^0\) = – 0.74V and \(\mathrm{E}_{\mathrm{Fe}^{2+} / \mathrm{Fe}}^0\) = 0.44 V.
Solution:
Given cell is
Cr | \(\mathrm{Cr}_{(0.1 \mathrm{M})}^{+3}\) || \(\mathrm{Fe}_{(0.01 \mathrm{M})}^{+2}\) | Fe
E0 of Cr+3/Cr = -0.74 V
E0 of Fe+2/Fe = -0.44 V
ECr+3/Cr = E0 + \(\frac{0.059}{3}\) log10 [Cr+3]
= -0.74 + \(\frac{0.059}{3}\) log 0.1
= -0.76 V
EFe+2/Fe = -0.44 + \(\frac{0.059}{2}\) log 0.01
= -0.44 – 0.059 = – 0.499 V
EMF of cell = ERHS – ELHS
= (- 0.499) – (-0.76) = 0.26 1 V .
Question 3.
Calculate the potential of a Zn – Zn2+ electrode in which the molarity of Zn2+ is 0.001 M. Given that \(\mathrm{E}_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^0\) = – 0.76 V
R = 8.314 JK-1 mol-1; F = 96500 C mol-1.
Solution:
Given electrode Zn | Zn+2(0.001m) \(\mathrm{E}_{\mathrm{Zn}^{+2} / \mathrm{Zn}}^0\) = -0.76V
Nemst equation is
E = E0 + \(\frac{2.303 \mathrm{RT}}{\mathrm{nF}}\) log [Mn+]
Given R = 8.314 J/K. mole
F = 96500 c/mole
E = E0 + \(\frac{0.059}{\mathrm{n}}\) log C
= -0.76 + \(\frac{0.059}{2}\) log 0.001
= -0.76 – \(\frac{0.059}{2}\) × 3
= – 0.76 – 0.0295 × 3
= -0.76 – 0.0885
= -0.8485 V
Question 4.
Determine ∆G0 for the button cell used in the watches. The cell reaction is
Zn(s) + Ag2O(s) + H2O(l)→ \(\mathrm{Zn}_{(a q)}^{2+}\) + 2 Ag(s) + 2 \(\mathrm{OH}_{(a q)}^{-}\)
\(\mathrm{E}_{\mathrm{Ag}^+ / \mathrm{Ag}}^0\) = + 0.80 V; \(\mathbf{E}_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^0\) = – 0.76 V.
Solution:
Given E0 of Ag+/Ag = 0.80 V
E0 of Zn+2/Zn = – 0.76 V
Cell representation Zn/Zn+2|| Ag+ / Ag
EMF = ERHS – ELHS = 0.80 – (-0.76) = 1.56 V
∆G = -nFE0 = -2 × 96500 × 1.56 = -301.08 kJ/mole
![]()
Question 5.
Calculate the emf of the cell consisting the following half cells
Al/Al3+(0.001 M), Ni/Ni2+ (0.50 M). Given that \(\mathrm{E}_{\mathrm{Ni}^{2+} / \mathrm{Ni}}^0\) = – 0.25 V \(\mathrm{E}_{\mathrm{Al}^{3+} / \mathrm{Al}}^0\) = – 1.66 v (log 8 × 10-6 = – 5.0969).
Solution:
Given E0 of Al+3/Al =-1.66 V
E0 of Ni+2/Ni = – 0.25 V
Cell representation Al/\(\mathrm{Al}_{(0.001 \mathrm{M})}^{+3}\) || \(\mathrm{Ni}_{(0.50 \mathrm{M})}^{+2}\) | Ni
Nemst equation is
EAl+3/Al = \(\mathrm{E}_{\mathrm{Al}^{+3} / \mathrm{A} l}^0\) + \(\frac{0.059}{n}\) log [Al+3]
= -1.66 + \(\frac{0.059}{3}\) log 0.001 = – 1.66 – 0.059 = – 1.719V
ENi+2/Ni = \(\mathrm{E}_{\mathrm{Ni}^{+2} / \mathrm{Ni}}^0+\frac{0.059}{\mathrm{n}}\) log [Ni+2]
= -0.25 + \(\frac{0.059}{2}\) log [0.5]
= -0.25 – 0.0295 × 0.3010 = -0.25 – 0.0088795 = -0.25888
EMF of cell = ERHS – ELHS
= -0.25888 – (-1.719) = 1.46012 V
Question 6.
Determine the values of Kc for the following reaction
Ni(s) + 2 \(\mathrm{Ag}_{\text {(aq) }}^{+}\) → \(\mathrm{Ni}_{\text {(aq) }}^{2+}\) + 2 Ag(s) E0 = 1.05 V.
Solution:
Given
Ni(s) + 2 \(\mathrm{Ag}_{\text {(aq) }}^{+}\) → \(\mathrm{Ni}_{\text {(aq) }}^{2+}\) + 2 Ag(s)
E0 = 1.05 V.
Nernst Equation is E = E0 – \(\frac{0.059}{\mathrm{n}}\) log Kc
at equilibrium E = 0
E0 = \(\frac{0.059}{\mathrm{n}}\) log Kc
1.05 = \(\frac{0.059}{2}\) log Kc
log Kc = \(\frac{2.1}{0.059}\) = 35.59
Kc = 3.42 × 1035
Question 7.
Calculate the potential of the half-cell containing 0.1 M
K2Cr2O7(aq), 0.2 M \(\mathrm{Cr}_{\mathrm{aq}}^{3+}\) and 1.0 × 10-4 M \(\mathrm{H}_{(\mathrm{aq})}^{+}\). The half-reaction \(\mathrm{Cr}_2 \mathrm{O}_{7(\mathrm{aq})}^{2-}+14 \mathrm{H}_{\text {(aq) }}^{+}+6 \mathrm{e}^{-} \longrightarrow 2 \mathrm{Cr}_{(\mathrm{aq})}^{3+}+7 \mathrm{H}_2 \mathrm{O}_{(l)}\) (E0 of \(\mathrm{Cr}_2 \mathrm{O}_7^{2-} / \mathrm{Cr}^{3+}\) = 1.33 V)
Solution:
Given half reaction

Question 8.
Calculate K for the reaction at 298 K
\(\mathrm{Zn}_{(\mathrm{s})}+\mathrm{Cu}_{(\mathrm{aq})}^{2+} \rightleftharpoons \mathrm{Zn}_{(\mathrm{aq})}^{2+}+\mathrm{Cu}_{(\mathrm{s})}\)
\(\mathrm{E}_{\mathrm{Zn}^{2+/ Z n}}^0\) = -0.76 V; \(\mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^0\) = + 0.34 V.
Solution:
Given \(\mathrm{Zn}_{(\mathrm{s})}+\mathrm{Cu}_{(\mathrm{aq})}^{2+} \rightleftharpoons \mathrm{Zn}_{(\mathrm{aq})}^{2+}+\mathrm{Cu}_{(\mathrm{s})}\)
E0 of Zn+2/Zn = -0.76 V
E0 of Cu+2/Cu = -0.34 V
E0 of cell = ERHS – ELHS = 0.34 – (- 0.76) = 1.1 V
∆G0 = – RTlnKc = – 2.303 RT log Kc
-212300 = -2.303 × 8.314 × 298 × log Kc
log Kc = \(\frac{212300}{2.303 \times 8.314 \times 298}\) = 37.207
Kc = 1.6 × 1037
![]()
Question 9.
Calculate the emf of the cell at 298 K
Sn(s) | Sn2+ (0.05 M) || \(\mathrm{H}_{(\mathrm{aq})}^{+}\) (0.02 M) | H2 1 atm. Pt
Given that \(\mathrm{E}_{\mathrm{Sn}^{2+} / \mathrm{Sn}}^0\) = -0.144 V
Solution:
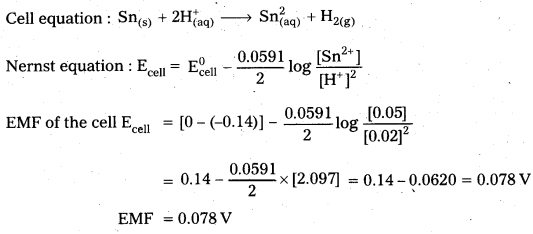
Question 10.
Calculate the concentration of silver ions in the cell constructed by using 0.1 M concentration of Cu2+ and Ag+ ions. Cu and Ag metals are used as electrodes. The cell potential is 0.422 V.
[\(\mathrm{E}_{\mathrm{Ag}^{2+} / \mathrm{Ag}}^0\) = 0.80 V; \(\mathrm{E}_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^0\) = +0.34 V]
Solution:
Given E0 of Ag+/Ag = 0.80 V .
E0 of Cu+2/Cu = 0.34 V
E0 of cell = ERHS – ELHS = 0.80 – 0.34 = 0.46 V

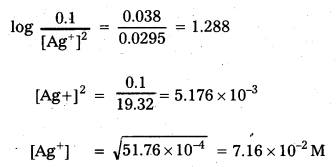
Question 11.
Calculate the emf of the cell with the cell reaction
Ni(s) + 2 Ag+ (0.002M) → Ni2+ (0.160 M) + 2 Ag(s) ; \(\mathrm{E}_{\text {cell }}^0\) = 1.05 V.
Solution:
From the given cell reaction and Nernst equation

![]()
Question 12.
Cu2+ + 2e– ⇌ Cu; E0 = +0.34 V
Ag+ + e– ⇌ Ag; E0 = + 0.80 V
For what concentration of Ag+ ions will the emf of the cell be zero at 25°C. The concentration of Cu2+ is 0.1 M. (log 3.919 = 0.593).
Solution:
Cell is Cu|Cu+2 | |Ag+|Ag
E0 of cell = ERHS – ELHS = 0.80 – 0.34 = 0.46 V
Nernst equation is E = E0 – \(\frac{0.059}{2} \log \frac{\left[\mathrm{Cu}^{+2}\right]}{\left[\mathrm{Ag}^{+}\right]^2}\)
EMF of cell = 0
E0 = \(\frac{0.059}{2} \log \frac{0.1}{\left[\mathrm{Ag}^{+}\right]^2}\)

Question 13.
The conductivity of 0.20 M solution of KCl at 298 K is 0.0248 S cm-1. Calculate molar conductance.
Solution:
Conductivity (K) = 0.0248 S cm-1 = 0.0248 ohm-1 cm-1
Molar concentration [c] = 0.20 mol L-1
= \(\frac{[0.2 \mathrm{~mol}]}{\left[1000 \mathrm{~cm}^3\right]}\) = 2.0 × 10-4 mol cm-3
Molar conductivity [∧m] = \(\frac{\kappa}{\mathrm{c}}=\frac{\left[0.0248 \mathrm{ohm}^{-1} \mathrm{~cm}^{-1}\right]}{\left[2.0 \times 10^{-4} \mathrm{~mol} \mathrm{~cm}^{-3}\right]}\)
= 124 ohm-1 mol-1 cm2 or 1245 mol-1 cm2
Molar conductivity = 124 mol-1 cm2
Question 14.
Calculate the degree of dissociation (α) of CH3COOH at 298 K.
Given that \(\wedge_{\mathrm{CH}_3 \mathrm{COOH}}^{\infty}\) = 11.75 cm2 mol-1
\(\wedge_{\mathrm{CH}_3 \mathrm{COO}^{-}}^0\) = 40.95 cm2 mol-1
\(\wedge_{\mathrm{H}^{+}}^0\) = 349.15 cm2 mol-1
Solution:
Given that \(\wedge_{\mathrm{CH}_3 \mathrm{COOH}}^{\infty}\) = 11.75 cm2 mol-1
\(\wedge_{\mathrm{CH}_3 \mathrm{COO}^{-}}^{\infty}\) = 40.95 cm2 mol-1
\(\wedge_{\mathrm{H}^{+}}^{\infty}\) = 349.15 cm2 mol-1
\(\wedge_{\mathrm{CH}_3 \mathrm{COOH}}^{\infty}\) = \(\wedge_{\mathrm{CH}_3 \mathrm{COO}^{-}}^{\infty}\) + \(\wedge_{\mathrm{H}^{+}}^{\infty}\) = 40.95 + 349.15 = 390.1
Degree of dissociation (α) = \(\frac{\lambda^\alpha}{\lambda^{\infty}}=\frac{11.75}{390: 1}\) = 0.03 = 3 × 10-2
∴ α = 3× 10-2
Textual Examples
Question 1.
Represent the cell in which the following reaction takes place Mg(s) + 2Ag+ (0.0001M) → Mg2+ (0.130M) + 2 Ag(s)
Calculate its E(cell) if \(\mathrm{E}_{(\text {cell) }}^{\Theta}\) = 3.17 V
Solution:
The cell is represented as Mg |Mg2+ (0.130M) || Ag+(0.0001M) | Ag
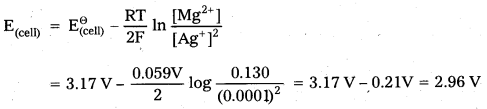
![]()
Question 2.
Calculate the equilibrium constant of the reaction:
Cu(s) + 2 \({Ag}_{\text {(aq) }}^{+}\) → \(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) + 2 Ag(s) ; \(\mathrm{E}_{(\text {cell) }}^{\Theta}\) = 0.46 V
Solution:
\(\mathrm{E}_{(\text {cell) }}^{\Theta}\) = \(\frac{0.059V}{2}\) log Kc = 0.46 V or
l0g Kc = \(\frac{0.46 \mathrm{~V} \times 2}{0.059 \mathrm{~V}}\) = 156
Kc = 3.92 × 1015
Question 3.
The standard emf of Daniell cell is 1.1V. Calculate the standard Gibbs energy for the cell reactions:
Zn(s) + \(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) → \(\mathrm{Zn}_{(\mathrm{aq})}^{2+}\) + Cu(s)
Solution:
∆rGΘ = -nF\(\mathrm{E}_{(\text {cell) }}^{\Theta}\)
n in the above equation is 2, F = 96487 C mol-1 and \(\mathrm{E}_{(\text {cell) }}^{\Theta}\) = 1.1 V
Therefore ∆rGΘ = -2 × 1.1V × 96487 C mol-1
= – 21227 J mol-1 =-212.27 kJ mol-1
Question 4.
Resistance of a conductivity cell filled with 0.1 mol L-1 KCl solution is 100 Ω. If .the resistance of the same cell when filled with 0.02 mol L-1 KCl solution is 520 Ω, calculate the conductivity and molar conductivity of 0.02 mol L-1 KCl solution. The conductivity of 0.1 mol L-1 KCl solution is 1.29 S/m.
Solution:
The cell constant is given by the equation :
Cell constant = G* = conductivity × resistance
= 1.29 S/m 100 Ω = 129 m-1 = 1.29 cm-1
Conductivity of 0.02 mol L-1 KCl solution = cell constant / resistance
= \(\frac{\mathrm{G}^*}{\mathrm{R}}=\frac{129 \mathrm{~m}^{-1}}{520 \Omega}\) = 0.248 S m-1
Concentration = 0.02 mol L-1
= 1000 × 0.02 mol m-3 = 20 mol m-3
Molar conductivity = ∧m = \(\frac{\kappa}{\mathrm{c}}\)
= \(\frac{248 \times 10^{-3} \mathrm{Sm}^{-1}}{20 \mathrm{~mol} \mathrm{~m}^{-3}}\) = 124 × 10-4 Sm2 mol-1
Alternatively, κ = \(\frac{1.29 \mathrm{~cm}^{-1}}{520 \Omega}\) = 0.248 × 10-2 S cm-1
and ∧m = κ × 1000 cm3L-1 molarity-1
= \(\frac{0.248 \times 10^{-2} \mathrm{~S} \mathrm{~cm}^{-1} \times 1000 \mathrm{~cm}^3 \mathrm{~L}^{-1}}{0.02 \mathrm{~mol} \mathrm{~L}^{-1}}\)
= 124 S cm2 mol-1
![]()
Question 5.
The electrical resistance of a column 0.05 mol L-1 NaOH solution of diameter 1 cm and length 50 cm is 5.55 × 103 ohm. Calculate its resistivity, conductivity and molar conductivity.
Answer:
A = πr2 = 31.4 × 0.52 cm2 = 0.785 cm2 = 0.785 × 10-4 m2
l = 50 cm = 0.5 m

Question 6.
Calculate \(\wedge_m^0\) for CaCl2 and MgSO4 from the data given in Table 3.4.
Solution:
We know from Kohlrausch law that
\(\wedge_{\mathrm{m}\left(\mathrm{CaCl}_2\right)}^0=\wedge_{\mathrm{Ca}^{2+}}^0+2 \lambda_{\mathrm{Cl}}^0\) = 119.0 S cm2 mol -1 + 2(76.3) S cm2 mol-1
= (119.0 + 152.6) Scm2 mol-1
= 271.6 S cm2 mol-1
\(\wedge_{\mathrm{m}\left(\mathrm{MgSO}_4\right)}^0=\lambda_{\mathrm{Mg}^{2+}}^0+\lambda_{\mathrm{SO}_4^{2-}}^0\) =106.0 S cm2 mol-1 + 160.0 S cm2 mol-1
= 266 S cm2 mol-1
Question 7.
\(\wedge_m^0\) for NaCl, HCl and NaAc are 126.4,425.9 and 91.0 S cm2 mol-1 respectively. Calculate ∧0 for HAc.
Solution:
\(\wedge_{\mathrm{m}(\mathrm{HAc})}^0=\lambda_{\mathrm{H}^{+}}^0+\lambda_{\mathrm{Ac}^0}^0=\lambda_{\mathrm{H}^{+}}^0+\lambda_{\mathrm{Cl}^{-}}^0+\lambda_{\mathrm{Na}^{+}}^0-\lambda_{\mathrm{Cl}^{-}}^0-\lambda_{\mathrm{Na}^{+}}^0\)
= \(\wedge_{\mathrm{m}(\mathrm{HCl})}^0+\wedge_{\mathrm{m}(\mathrm{NaAc})}^0-\wedge_{\mathrm{m}(\mathrm{NaCl})}^0\)
= (425.9 + 91.0 – 126.4) S cm2 mol-1
= 390.5 S cm2 mol-1
Question 8.
The conductivity of 0.001028 mol L-1 acetic acid is 4.95 × 10-5 S cm-1. Calculate its dissociation constant if \(\wedge_m^0\) for acetic acid is 390.5 S cm2 mol-1.
Solution:
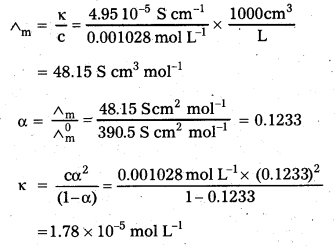
![]()
Question 9.
A solution of CuSO4 is electrolysed for 10 minutes with a current of 1.5 amperes. What is the mass of eopper deposited at the cathode ? [A.P. & T.S. Mar. 15] [Mar. 15]
Solution:
t = 600 s charge = current × time = 1.5A × 600 s = 900 C
According to the reaction :
\(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) + 2e– = Cu(s)
We require 2F or 2 × 96487 C to deposit 1 mol or 63 g of Cu.
For 900 C, the mass of Cu deposited
= (63 g mol-1 × 900 C) / (2 × 96487 C mol-1) = 0.2938 g
Intext Questions
Question 1.
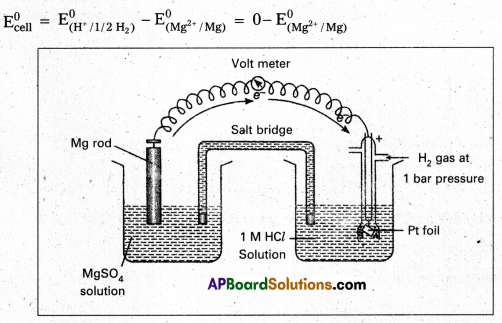
How would you determine the standard electrode potential of the system Mg2+/Mg ?
Solution:
E° value of Mg2+/Mg electrode is determined by setting up an electrochemical cell. For this purpose, a Mg electrode is dipped in 1 M MgSO4 solution, which acts as one half cell i.e., oxidation half-cell.
In the same way, the standard hydrogen electrode acts as the other half-cell i.e., reduction half cell. The deflection of voltmeter placed in the cell circuit is towards the Mg electrode which indicates the direction of flow of current.
The cell may be represented as : Mg | Mg2+ (1M) || H+ (M) | H2 (1 atm). Pt The reading as given by voltmeter gives \(\mathrm{E}_{\text {cell }}^0\)
Question 2.
Can you store copper sulphate solutions In a zinc pot?
Solution:
No, zinc pot cannot store copper sulphate solutions because the standard electrode potential (E0) value of zinc is less than that of copper. So, zinc is stronger reducing agent then copper.
\(\mathrm{Zn}_{(\mathrm{aq})}^{2+}\) + 2e– → Zn(s); E0 = -0.76 V
\(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) + 2e– → Cu(s); E0 = – 0.34 V
So, zinc will loss electrons to Cu2+ ions and redox reaction will occur as follows.
Zn(s) + \(\mathrm{Cu}_{(\mathrm{aq})}^{2+}\) → \(\mathrm{Zn}_{(\mathrm{aq})}^{2+}\) + Cu(s)
![]()
Question 3.
Consult the table on standard electrode potentials and suggest three substances that can oxidise ferrous ions under suitable conditions.
Solution:
Fe2+ (ferrous) ions gets oxidised to Fe3+ (ferric) ion as follows
Fe2+ → Fe3+ + e– \(\mathrm{E}_{0 \mathrm{x}}^0\) = -0.77V
Only those substances can oxidise Fe2+ ions to Fe3+ ions which can accept electrons released during oxidation or are placed above iron in electrochemical series. Three such substances are: Cl2(g), Br2(g) and F2(g).
Question 4.
Calculate the potential of hydrogen electrode placed in a solution of pH 10.
Solution:

Question 5.
The cell in which the following cell reaction occurs,
\(2 \mathrm{Fe}_{(\mathrm{aq})}^{3+}+2 \mathrm{I}_{(\mathrm{aq})}^{-} \longrightarrow 2 \mathrm{Fe}_{(\mathrm{aq})}^{2+}+\mathrm{I}_{2(\mathrm{~s})}\) has \(\mathrm{E}_{\text {cell }}^0\) = 0.236 V at 298 K. Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.
Solution:
Two half reactions for the given redox reaction may be written as :
\(2 \mathrm{Fe}_{(\mathrm{aq})}^{3+}+2 \mathrm{e}^{-} \longrightarrow 2 \mathrm{Fe}_{(\mathrm{aq})}^{2+} ; 2 \mathrm{I}^{-} \longrightarrow \mathrm{I}_2+2 \mathrm{e}^{-}\)
2 moles of electrons are involved in the reaction, so n = 2
∆rG0 = – nF\(\mathrm{E}_{\text {cell }}^0\) = (-2 mol) × (96500 mol-1) (0.236 V)
= -45548 CV = -45548 J
∆rG0 = – 45.55 kJ
log Kc = \(\frac{\Delta \mathrm{G}^0}{2.303 \mathrm{RT}}\)
= \(\frac{(-45.55 \mathrm{~kJ})}{2.303 \times\left(8.314 \times 10^{-3} \mathrm{kJK}^{-1}\right) \times(298 \mathrm{~K})}\) = 7.983
Kc = Antilog (7.983) = 9.616 × 107
Kc = 9.616 × 107
![]()
Question 7.
Why does the conductivity of a solution decrease with dilution ?
Solution:
The conductivity of a solution is related with the number of ions present per unit volume of the solution. When the solution is diluted, the number of ions decreases. Hence, conductivity or specific conductance of the solution also decreases.
Question 8.
Suggest a way to determine the \(\wedge_{\mathrm{m}}^0\) value of water.
Solution:
The molar conductance of water at infinite dilution can be obtained from the knowledge of molar conductances at inifite dilution of sodium hydroxide, hydrochloric acid and sodium chloride (all strong electrolytes). This is in accordance with Kohlrausch’s law.
\(\wedge_{\mathrm{m}\left(\mathrm{H}_2 \mathrm{O}\right)}^0=\wedge_{\mathrm{m}(\mathrm{NaOH})}^0+\wedge_{\mathrm{m}(\mathrm{HCl})}^0-\wedge_{\mathrm{m}(\mathrm{NaCl})}^0\)
Question 9.
The molar conductivity of 0.025 mol L-1 methanoic acid is 46.1 S cm2 mol-1. Calculate its degree of dissociation and dissociation constant.
Given, λ0(H+) = 349.6 S cm-1 mol-1 and λ0 (HCOO–) = 54.6 S cm2 mol-1
Solution:
Step I: Calculation of degree of dissociation (a) of HCOOH

= \(\frac{\left(3.249 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}\right)}{(0.886)}\)
= 3.67 × 10-4 mol L-1
α = 0.114
Ka = 3.67 × 10-4 mol L-1
Question 10.
If a current of 0.5 ampere flows through a metallic wire for 2h, then how many electrons would flow through the wire ?
Solution:
Quantity of charge (Q) passed = Current (C) × Time (t)
= (0.5 A) × (2 × 60 × 60 s)
= (3600) Ampere sec = 3600 C ,
Number of electrons flowing through the wire on passing charge of one Faraday (96500 C) = 6.022 × 1023
Number of electrons flowing through the wire on passing a charge of 3600 C
= \(\frac{6.022 \times 10^{23} \times(3600 \mathrm{C})}{(96500 \mathrm{C})}\)
= 2.246 × 1022
Number of electrons = 2.246 × 1022
![]()
Question 11.
Suggest a list to metals that are extracted electrolytically.
Solution:
Those metals which are highly reactive and have large negative E0 values can be exerted electrolytically. This type of metals are powerful reducing agents.
Eg: Sodium, Potassium, Calcium, Magnesium etc.
Question 12.
Consider the reaction,
\(\mathrm{Cr}_2 \mathrm{O}_7^{2-}\) + 14H+ + 6e– → 2Cr3+ + 7H2O
What is the quantity of electricity in coulombs nefeded to reduce 1 mole of \(\mathrm{Cr}_2 \mathrm{O}_7^{2-}\) ?
Solution:
1 mole \(\mathrm{Cr}_2 \mathrm{O}_7^{2-}\) require 6 Faraday electricity (6 F)
= 6 × 96500 C = 5.79 × 105 C
Quantity of electricity = 5.79 × 105 Coulomb
Question 13.
Write the chemistry of recharging the lead storage battery, highlighting all the materials that are involved during recharging.
Solution:
When lead storage battery is recharged, electrical energy is supplied to the cell from the external source : i.e., the cell operates as an electrolytic cell during recharging. All the chemical reactions, which take place during the use of battery, are reversed at this time.
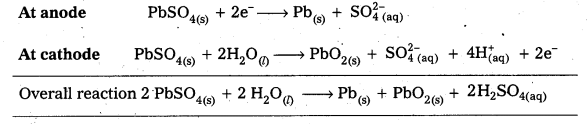
Question 14.
Suggest two materials other than hydrogen that can be used as fuels in fuel cells.
Solution:
Methane (CH4) and methanol (CH3OH)
![]()
Question 15.
Explain how rusting of iron is envisaged as setting up of an electrochemical cell.
Solution:
In corrosion, a metal is oxidised by loss of electrons to oxygen with the formation of oxides. So, an electrochemical cell is set up.
Eg: Rusting of iron involves the following steps :
i) The water layer present on the surface of iron dissolves acidic oxides from air like CO2 and forms acid to produce H+ ions.
H2O + CO2 H2CO3 ⇌ 2H+ + \(\mathrm{CO}_3^{2-}\)
ii) In the presence of H+ ions, iron starts losing electrons at some spot to form ferrous ions. This spot behaves as anode.
![]()
iii) The electrons released at anode move to another spot, where H+ ions and the dissolved oxygen gain these electrons. This spot becomes a cathode.
![]()
iv) Overall reaction, i.e., redox reaction is :
![]()
v) Ferrous ions are further oxidised by the atmospheric oxygen to ferric ions which combine with water molecules to form hydrated ferric oxide, Fe2O3. xH2O. (Rust).