AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.4
Question 1.
In the given triangles, find out ∠x, ∠y and ∠z
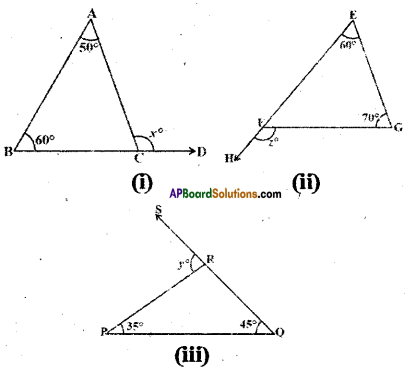
Solution:
In fig(i)
x° = 50° + 60°
(∵ exterior angle is equal to sum of the opposite interior angles)
∴ x= 110°
In fig (ii)
z° = 60° + 70°
(∵ exterior angle is equal to sum of the opposite interior angles)
∴ z = 130°
In fig (iii)
y° = 35° + 45° = 80°
(∵ exterior angle is equal to sum of the opposite interior angles)
![]()
Question 2.
In the given figure AS // BT; ∠4 = ∠5, \(\overline{\mathbf{S B}}\) bisects ∠AST. Find the measure of ∠1.
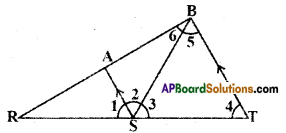
Solution:
Given AS // BT
∠4 = ∠5 and SB bisects ∠AST.
∴ By problem
∠2 = ∠3 …………..(1)
For the lines AS // BT
∠2 = ∠5 ( ∵alternate interior angles)
∴ In ΔBST
∠3 = ∠5 = ∠4
Hence ΔBST is equilateral triangle and each of its angle is equal to 60°.
∴∠3 = ∠2 = 60° [by eq. (1)]
Now ∠1 + ∠2 + ∠3 = 180°
∠1 + 60° + 60° = 180°
[ ∵ angles at a point on a line]
∴∠1 = 180° – 120° = 60°
Question 3.
In the given figure AB // CD; BC // DE then find the values of x and y.
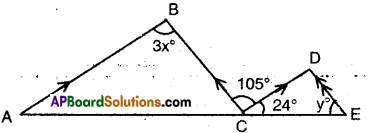
Solution:
Given that AB // CD and BC // DE.
∴ 3x = 105° (∵ alternate interior angles for AB // CD)
x = \(\frac { 105° }{ 3 }\) = 35°
Also BC // DE
∴∠D = 105°
(∵ alternate interior angles)
Now in ΔCDE
24° + 105° + y = 180°
(∵ angle sum property)
∴ y = 180° – 129° = 51°
![]()
Question 4.
In the given figure BE ⊥ DA and CD ⊥ DA then prove that m∠1 = m∠3.
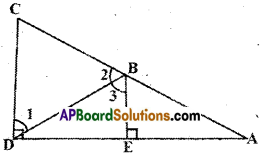
Solution:
Given that CD ⊥ DA and BE ⊥ DA.
⇒ Two lines CD and BE are perpendicular to the same line DA.
⇒ CD // BE (or)
∠D =∠E ⇒ CD // BE
(∵ corresponding angles for CD and BE and DA are transversal)
Now m∠1 = m∠3
(∵alternate interior angles for the lines CD // BE ; DB are transversal)
Hence proved.
Question 5.
Find the values of x, y for which lines AD and BC become parallel.
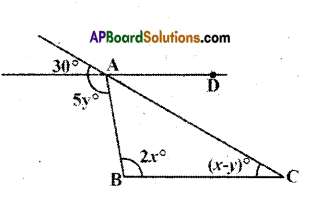
Solution:
For the lines AD and BC to be parallel x – y = 30° (corresponding angles) ……… (1)
2x = 5y ………….(2)
(∵ alternate interior angles)
Solving (1) & (2)
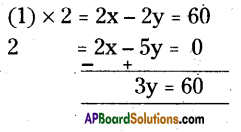
y = \(\frac{60}{3}\) = 20°
Substituting y = 20° in eq. (1)
x – 20° = 30°
⇒ x = 50°
∴ x = 50° and y = 20°
![]()
Question 6.
Find the values of x and y in the figure.
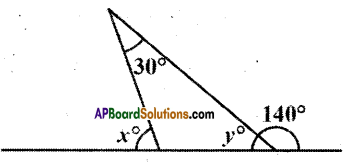
Solution:
From the figure y + 140° = 180°
(∵ linear pair of angles)
∴ y = 180° – 140° = 40°
And x° = 30° + y°
(∵ exterior angle = sum of the opposite interior angles)
x° = 30° + 40° = 70°
Question 7.
In the given figure segments shown by arrow heads are parallel. Find the values of x and y.
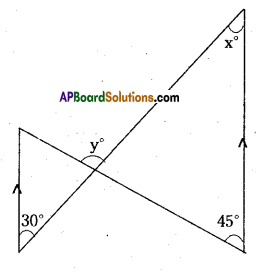
Solution:
From the figure
x° = 30° (∵ alternate interior angles)
y° = 45° + x° (∵ exterior angles of a triangle = sum of opp. interior angles)
y = 45° + 30° – 75°
Question 8.
In the given figure sides QP and RQ of ∠PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
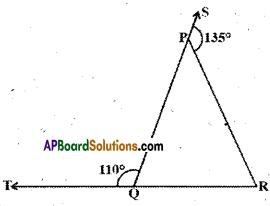
Solution:
Given that ∠SPR = 135° and ∠PQT =110°
From the figure
∠SPR + ∠RPQ = 180°
∠PQT + ∠PQR = 180°
[∵ linear pair of angles]
⇒ ∠RPQ = 180° – ∠SPR
= 180° – 135° = 45°
⇒ ∠PQR = 180° – ∠PQT
= 180°-110° = 70°
Now in APQR
∠RPQ + ∠PQR + ∠PRQ = 180°
[∵ angle sum property]
∴ 45° + ’70° + ∠PRQ = 180°
∴ ∠PRQ = 180°-115° = 65°
![]()
Question 9.
In the given figure ∠X = 62° ; ∠XYZ = 54°. In ΔXYZ. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respec-tively find ∠OZY and ∠YOZ.
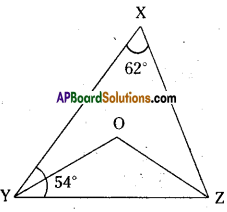
Solution:
Given that ∠X = 62° and ∠Y = 54°
YO arid ZO are bisectors of ∠Y and ∠Z.
In ΔXYZ
∠X + ∠XYZ + ∠XZY = 180° .
62° + 54° + ∠XZY = 180°
=> ∠XZY = 180°- 116° = 64°
Also in Δ𝜏OYZ
∠OYZ = 1/2 ∠XYZ = 1/2 x 54° = 27°
(∵ YO is bisector of ∠XYZ)
∠OZY = 1/2 ∠XZY = 1/2 x 64° = 32
(∵ OZ is bisector of ∠XYZ)
And ∠OYZ + ∠OZY + ∠YOZ = 180°
(∵ angle sum property, ΔOYZ)
⇒ 27 + 32° + ∠YOZ = 180°
⇒ ∠YOZ = 180° – 59° = 121°
Question 10.
In the given figure if AB // DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
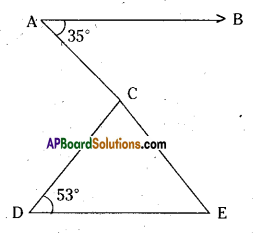
Solution:
Given that AB // DE, ∠CDE = 53°;
∠BAC = 35°
Now ∠E = 35°
( ∵ alternate interior angles)
Now in ∆CDE
∠C + ∠D + ∠E = 180°
(∵angle sum property, ACDE)
∴ ∠DCE + 53° + 35° = 180°
⇒ ∠DCE = 180° – 88° = 92°
![]()
Question 11.
In the given figure if line segments PQ and RS intersect at point T, such that∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
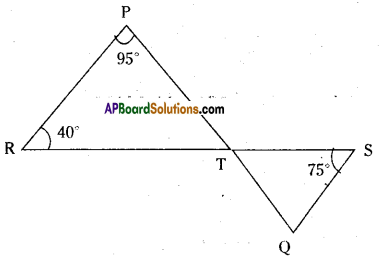
Solution:
Given that ∠PRT = 40°; ∠RPT = 95°;
∠TSQ = 75°
In ∆PRT ∠P + ∠R + ∠PTR = 180°
(∵angle sum property)
95° + 40° + ∠PTR = 180°
⇒ ∠PTR = 180° – 135° = 45°
Now ∠PTR = ∠STQ
(∵ vertically opposite angles)
In ΔSTQ ∠S + ∠Q + ∠STQ = 180°
(∵ angle sum property)
75° + ∠SQT + 45° = 180°
∴ ∠SQT = 180° – 120° = 60°
Question 12.
In the given figure, ABC is a triangle in which ∠B = 50° and ∠C = 70°. Sides AB and AC are produced. If ∠ is the measure of angle between the bisec¬tors of the exterior angles so formed, then find ‘z’.
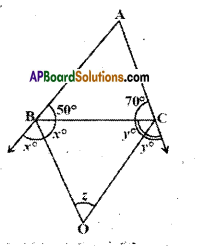
Solution:
Given that ∠B = 50°; ∠C = 70°
Angle between bisectors of exterior angles B and C is ∠.
From the figure
50° + 2x = 180°
70° + 2y = 180°
(∵ linear pair of angles)
∴ 2x= 180°-50°
2x= 130°
x = \(\frac{130}{2}\)
= 65°
2y= 180°-70°
2y= 110°
x = \(\frac{110°}{2}\)
= 55°
Now in ΔBOC
x + y + ∠ = 180° (∵ angle sum property)
65° + 55° + ∠ = 180°
z = 180° -120° = 60°
![]()
Question 13.
In the given figure if PQ ⊥ PS; PQ // SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
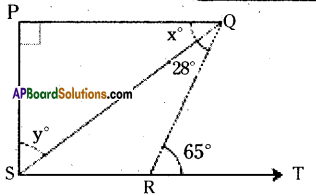
Solution:
Given that PQ ⊥ PS ; PQ // SR
∠SQR = 28°, ∠QRT = 65°
From the figure
∠QSR = x° (∵ alt. int. angles for the lines PQ // SR)
Also 65° = x + 28° (∵ ext. angles = sum of the opp. interior angles)
∴ x° = 65° – 28° = 37°
And x° + y° = 90°
[ ∵ PQ ⊥ PS and PQ // SR. ⇒ ∠P = ∠S]
37° + y = 90°
∴ y = 90° – 37° = 53°
Question 14.
In the given figure ΔABC side AC has been produced to D. ∠BCD = 125° and ∠A: ∠B = 2:3, find the measure of ∠A and ∠B
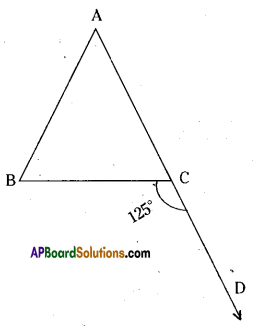
Solution:
Given that ∠BCD = 125°
∠A : ∠B = 2 : 3
Sum of the terms of the ratio
∠A : ∠B = 2 + 3 = 5
We know that ∠A + ∠B = ∠BCD
(∵ exterior angles of triangle is equal to sum of its opp. interior angles)
∴ ∠A = \(\frac{2}{5}\) x 125° = 50°
∠B = \(\frac{3}{5}\) x 125° = 75°
Question 15.
In the given figure, it is given that, BC // DE, ∠BAC = 35° and ∠BCE = 102°. Find the measure of 0 ∠BCA i0 ∠ADE and iii) ∠CED.
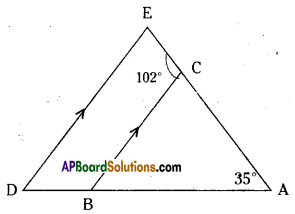
Solution:
Given that BC // DE ; ∠BAC = 35°;
∠BCE = 102°
i) From the figure
102° + ∠BCA = 180°
(∵ linear pair of angles)
∴ ∠BCA = 180° – 102° = 78°
![]()
ii) ∠ADE + ∠CBD = 180°
(∵ interior angles on the same side of the transversal)
∠ADE + (78° + 35°) = 180°
(∵ ∠CBD = ∠BAC + ∠BCA)
∴ ∠ADE = 180° – 113° = 67°
iii) From the figure .
∠CED = ∠BCA = 78°
(∵ corresponding angles)
Question 16.
In the given figure, it is given that AB = AC; ∠BAC = 36°; ∠ADB = 45° and ∠AEC = 40°. Find i) ∠ABC
i) ∠ACB iii) ∠DAB iv) ∠EAC.
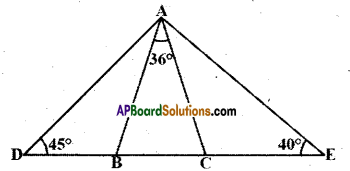
Solution:
Given that AB = AC; ∠BAC = 36°,
∠ADB = 45°, ∠AEC = 40°
(i) & (ii)
In ∆ABC ; AB = AC
⇒ ∠ABC = ∠ ACB
And 36° + ∠ABC + ∠ACB = 180°
(∵ angle sum property)
∴ ∠ABC = \(\frac{180^{\circ}-36^{\circ}}{2}=\frac{144^{\circ}}{2}=72^{\circ}\)
∠ACB = 72°
iii) From the figure
∠ABD + ∠ABC = 180°
∠ABD = 180° – 72° = 1086
In ΔABD
∠DAB + ∠ABD + ∠D = 180°
∠DAB + 108° + 45° = 180°
∠DAB = 180° – 153° = 27°
![]()
iv) In ΔADE
∠D + ∠A + ∠E = 180°
45° + ∠A + 40° = 180°
⇒ ∠A = 180° -85° = 95°
But ∠A = ∠DAB + 36° + ∠EAC
95° = 27°, + 36° + ∠EAC
∴ ∠EAC = 95° – 63° = 32°
Question 17.
Using information given in the figure, calculate the values of x and y.
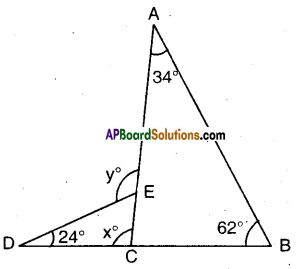
Solution:
From the figure In ∆ACB
34° + 62° + ∠ACB = 180°
(∵ angle sum property)
∴ ∠ACB = 180° – 96° = 84° .
And x + ∠ACB = 180°
(∵ linear pair of angles) .
∴ x + 84° = 180°
x = 180°-84° = 96°
(OR)
x = 34° + 62° = 96°
( ∵ x is exterior angle, ∆ABC)
y = 24° + x°
= 24° + 96° = 120°
(∵ y is exterior angle, ∆DCE)
