AP State Syllabus AP Board 9th Class Maths Solutions Chapter 11 Areas Ex 11.2 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 11th Lesson Areas Exercise 11.2
![]()
Question 1.
The area of parallelogram ABCD is 36cm2. Calculate the height of parallelogram ABEF if AB = 4.2 cm.
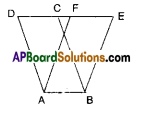
Solution:
Area of □ABCD = 36 cm2
AB = 4.2 cm
then □ABCD = AB X Height
[ ∵ base x height]
36 = 4.2 x h
∴ h = \(\frac { 36 }{ 4.2 }\)
But □ ABCD and □ ABEF are on the same base and between the same parallels.
∴ □ABCD = □ABEF
□ABEF = base x height = AB x height
∴ height = \(\frac { 36 }{ 4.2 }\) = 8.571cm 5
Question 2.
ABCD is a parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB = 10 cm; AE = 8 cm and CF = 12 cm. Find AD.
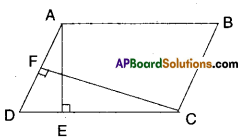
Solution:
Area of parallelogram = base x height
AB x AE = AD x CF
⇒ 10 x 8 = 12 x AD
⇒ AD = \(\frac{10 \times 8}{12}\) = 6.666 ……….
∴ AD ≅ 6.7 cm
![]()
Question 3.
If E, F, G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar (EFGH) = \(\frac { 1 }{ 2 }\) ar (ABCD).
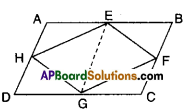
Solution:
Given that □ABCD is a parallelogram.
E, F, G and H are the midpoints of the sides.
Join E, G.
Now
ΔEFG and □EBCG he on the same base EG and between the same parallels
EG // BC.
∴ ΔEFG = \(\frac { 1 }{ 2 }\)□EBCG ……………(1)
Similarly,
ΔEHG = \(\frac { 1 }{ 2 }\)□EGDA …………….(2)
Adding (1) and (2);
ΔEFG + ΔEHG = \(\frac { 1 }{ 2 }\) □EBCG + \(\frac { 1 }{ 2 }\) □EGDA
□EFGH = \(\frac { 1 }{ 2 }\)[□EBCG +□ EGDA]
□EFGH = \(\frac { 1 }{ 2 }\) [□ABCD]
Hence proved.
Question 4.
What figure do you get, if you join ΔAPM, ΔDPO, ΔOCN and ΔMNB in the example 3 ?
Solution:
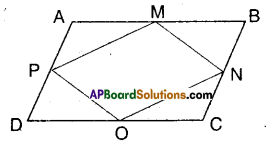
□ABCD is a rhombus.
M, N, O and P are the midpoints of its sides. By joining ΔAPM, ΔDPO, ΔOCN and ΔMNB we get the figure shown by shaded region.
![]()
Question 5.
P and Q are any two points lying on the sides DC and AD .respectively of a parallelogram ABCD. Show that ar (ΔAPB) = ar (ΔBQC).
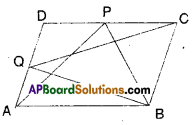
Solution:
ΔAPB and □ABCD are on the same base
AB and between the same parallel lines
AB//CD.
∴ ΔAPB = \(\frac { 1 }{ 2 }\) □ABCD …………… (1)
Also ΔBCQ and □BCDA are on the same base BC and between the same paral¬lel lines BC//AD.
∴ ΔBCQ = \(\frac { 1 }{ 2 }\) □BCDA …………….. (2)
But □ABCD and □BCDA represent same parallelogram.
∴ΔAPB = ΔBCQ [from (1) & (2)]
Question 6.
P is a point in the interior of a parallelogram ABCD. Show that
i) ar (ΔAPB) + ar (ΔPCD) = \(\frac { 1 }{ 2 }\)ar(ABCD)
(Hint : Through P, draw a line paral¬lel to AB)
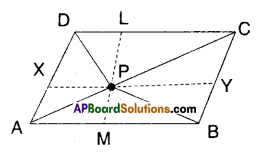
Solution:
□ABCD is a parallelogram.
P is any interior point.
Draw a line \(\overline{\mathrm{XY}}\) parallel to AB through P.
Now ΔAPB = \(\frac { 1 }{ 2 }\) □AXYB ……………(1)
[∵ ΔAPB, □AXYB lie on the same base AB and beween AB//XY]
Also ΔPCD = \(\frac { 1 }{ 2 }\) □CDXY ………………… (2)
[ ∵ ΔPCD; □CDXY lie on the same
base CD and between CD//XY]
Adding (1) & (2), we get
Δ APB + ΔPCD = \(\frac { 1 }{ 2 }\) □AXYB + \(\frac { 1 }{ 2 }\) □CDXY
= \(\frac { 1 }{ 2 }\) [□ AXYB + □ CDXY] [from the fig.)
= \(\frac { 1 }{ 2 }\) □ABCD
Hence Proved.
![]()
(ii) ar (ΔAPD) + ar (ΔPBQ = ar (ΔAPB) + ar (ΔPCD)
Solution:
Draw LM // AD.
ΔAPD + ΔPBC = \(\frac { 1 }{ 2 }\) □AMLD + \(\frac { 1 }{ 2 }\) □BMLC
= \(\frac { 1 }{ 2 }\) [□AMLD + \(\frac { 1 }{ 2 }\) BMLC].
= \(\frac { 1 }{ 2 }\) □ABCD
= ΔAPB +ΔPCD [from(i)]
Hence proved.
[ ∵ ΔAPD, □AMLD are on same base AD and between same parallels AD and LM]
Question 7.
Prove that the area of a trapezium is half the sum of the parallel sides mul¬tiplied by the distance between them.
Solution:
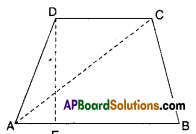
Let □ABCD is a trapezium; AB//CD and
DE ⊥ AB
□ABCD = ΔABC + ΔADC
= \(\frac { 1 }{ 2 }\) AB x DE + \(\frac { 1 }{ 2 }\) DC x DE
[∵ Δ = \(\frac { 1 }{ 2 }\) x base x height]
= \(\frac { 1 }{ 2 }\) x DE [AB + DC]
Hence proved.
![]()
Question 8.
PQRS and ABRS are parallelograms and X is any point on the side BR.
Show that
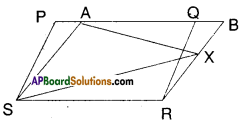
i) ar (PQRS) = ar (ABRS)
Solution:
□PQRS and □ABRS are on the same base SR and between the same parallels SR//PB.
∴ □PQRS = □ABRS
ii) ar (ΔAXS) = \(\frac { 1 }{ 2 }\) ar (PQRS)
Solution:
From (1) □PQRS = □ABRS
And □ABRS and ΔAXS are on the same base AS and between the same paral¬lels AS//BR.
∴ ΔAXS = \(\frac { 1 }{ 2 }\) □ABRS
= \(\frac { 1 }{ 2 }\) □PQRS from (1)
Hence proved.
![]()
Question 9.
A farmer has a held in the form of a parallelogram PQRS as shown in the figure. He took the midpoint A on RS and joined it to points P and Q. In how many parts the field is divided ? What are the shapes of these parts ? The farmer wants to sow groundnuts which are equal to the sum of pulses and paddy. How should he sow ? State reasons.
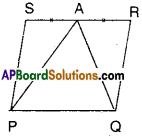
Solution:
From the figure ΔAPQ, □PQRS are on the same base PQ and between the same parallels PQ//SR.
∴ ΔAPQ = \(\frac { 1 }{ 2 }\)□PQRS
⇒ □PQRS – AAPQ = \(\frac { 1 }{ 2 }\)□PQRS
∴ \(\frac { 1 }{ 2 }\)□PQRS = ΔASP + ΔARQ
∴ The farmer may sow groundnuts on ΔAPQ region.
The farmer may sow pulses on ΔASP region.
The farmer may sow paddy on ΔARQ region.
![]()
Question 10.
Prove that the area of a rhombus is equal to half of the product of the diagonals.
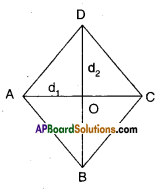
Solution:
Let □ABCD be a Rhombus.
d1, d2 are its diagonals bisecting at ‘O’
We know that d1 ⊥ d1
∴ ΔABC = \(\frac{1}{2} \mathrm{~d}_{1} \cdot\left(\frac{\mathrm{d}_{2}}{2}\right)\)
[∵ base = d1; height = \frac{\mathrm{d}_{2}}{2}[/latex] ]
ΔADC = \(\frac{1}{2} \mathrm{~d}_{1} \cdot\left(\frac{\mathrm{d}_{2}}{2}\right)\)
[ ∵ base = d1;height= \(\frac{\mathrm{d}_{2}}{2}\)]
∴ □ABCD = ΔABC + ΔADC
= \(\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{4}+\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{4}=\frac{\mathrm{d}_{1} \mathrm{~d}_{2}}{2}\)
Hence Proved.
