SCERT AP Board 8th Class Social Solutions 9th Lesson Public Health and the Government Textbook Questions and Answers.
AP State Syllabus 8th Class Social Studies Solutions 9th Lesson Public Health and the Government
8th Class Social Studies 9th Lesson Public Health and the Government Textbook Questions and Answers
Improve your learning
Question 1.
Correct the false statements.
a. Most rural areas have trained doctors.
b. There are more facilities in hospitals of private sector than the public sector.
c. Nutritious food helps in improving the health scenario.
d. Some doctors may involve in unnecessary treatments to make money.
Answer:
a) Most rural areas have trained doctors. (False)
Correction: Most rural areas have untrained doctors.
b) True
c) True
d) True
![]()
Question 2.
Jayamma uses the following. Which of these will you include in basic public facilities?
a. Drives Scooter to school,
b. Sends her child to Anganwadi.
c. Owns a television set.
d. Has a mobile phone,
e. Sends letters by post office.
Answer:
b. Sends her child to Anganwadi.
c. Sends letters by post office.
Question 3.
Identify the sentences in this chapter that discuss the role of the government in providing public health.
Answer:
“Self exercise” – The student should underline the sentences in this chapter.
Question 4.
Discuss which among the following measures will you consider as instances – OR not an instance of improving the healthcare. Write down the reasons for your answer.
a. TB patients are given free medicines.
b. In some villages clean drinking water facilities are arranged.
c. Shopkeepers selling medicines for cold, fever, headache etc.
d. The government provides foodgrains in Fair Price shops.
Answer:
I consider a, b, d as instances of improving the health care. Selling medicines by shop-keepers is trade.
![]()
Question 5.
Priyamvada runs a private hospital. This has more facilities than that are available in a government hospital. Satyanarayana works as a government doctor in a Mandal. Can you write an imaginary dialogue between them about access to health services?
Answer:
Priyamvada: Hello Doctor, how are you?
Satyanarayana: Fine doctor. You are working in?
Priyamvada: I run my own hospital in the town. You?
Satyanarayana: I am working in the government Mandai Hospital here?
Prlyamvada: Oh I am very sorry. All of our friends opened many super specialty hospitals and are running them successfully. But you…?
Satyanarayana: Oh I Don’t say sorry. This is my ambition.
Priyamvada: What is this doctor? We are working regularly in one hospital while visiting four to five others daily. A handful of income, sophisticated facilities. We have everything what we need. Operation theatres, oxygen facilities, ambulances etc. All the facilities are in our reach. Why
are you missing them?
Satyanarayana: Sorry Miss. Pnyamvada. I like my profession and this job. The people in villages are approaching untrained persons for treatment. We are in this profession to serve the people only.
It is the same either in villages or in towns. We have also many facilities in our hospitals.
Priyamvada: Very sorry doctor, very sorry. I misunderstand you. You are rendering more services to the people who are in need.
Now onwards I also will come and treat the patients without fees. All the best doctor.
![]()
Question 6.
Health is not limited to providing medicines. In this chapter there are other aspects of health that are mentioned (like clean water etc). Bring them together and write a paragraph about such aspects.
Answer:
Health is not limited to providing medicines only. The people should be given nutritious food. Safety Drinking water facilities should be arranged. First aid should be provided to the needy. Proper housing facilities, healthy environment should be created. Through these steps alone we can get good health.
Question 7.
Following figure shows how people get money for hospitalization in Andhra Pradesh. Nearly 65% of the people below poverty line have to borrow money. Identify this in the chart and mark the percentage. Those above poverty line spend 45% of the hospitalization expenditure from their savings. Identify this in the chart and mark the percentage. Those above poverty line borrow only 35%. Identify this in the chart and mark the percentage.
Can you also roughly estimate share of other means through which people meet their hospitalization expenses in the chart below?
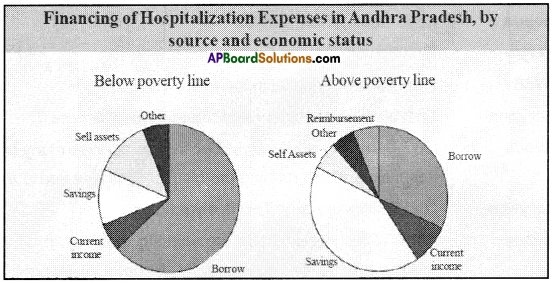 Answer:
Answer:
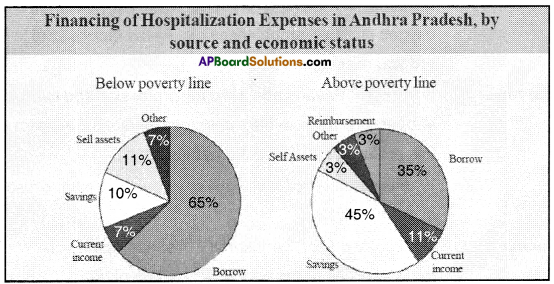
| Below the poverty line | Above the poverty line | ||
| Others | 7% | Others | 3% |
| Self assets | 11% | Self assets | 3% |
| Savings | 10% | Reimbursement | 3% |
| Borrow | 65% | Savings | 45% |
| Current income | 7% | Borrow | 35% |
| Current income | 11% | ||
They find their money for hospitalization as above.
![]()
Question 8.
Conduct a survey on government welfare schemes on health. List the beneficiaries in your area.
Answer:
- Aarogya Sri Scheme: White card holders.
- ESI: People working in public & private companies, factories etc.
- Reimbursement facilities: To State/Central government employees.
Question 9.
To know about the prevention of contageous diseases, what questions do you ask your region’s Health worker?
Answer:
- How can we prevent Malaria?
- What is the preventive medicine for Typhoid?
- Is there any preventive drug for Cholera?
- What are the preventive steps of govt, to control eye diseases?
Question 10.
What type of services would be rendered by ‘108′ during emergencies?
Answer:
All types of emergency cases are handled by 108 services, including pregnancy cases, accidental, unconscious, paralysis, inflation, fever, heart attack and all types of emergencies.
![]()
Project
Consult any five of your friends and fill the table with the following particulars, then analyse and discuss In the class.
| Sl.No. | Name of the student | How often the nails are cut? | How often the hands are washed? | Where are the leftover food items throwning mid-day meais? | How often he/she participates in school cleanliness? | What kinds of work they do for dean Siness of their houses? |
| 1. | Saroja | Once in a week | Each time before eating | In dustbin | Once in a month | Grooming |
| 2. | Dhanush | Once in a week | 3 – 4 times | In drain | Once in 6 – months | Not interested |
| 3. | Sarath | 10 – days | 5 – 8 times | Nil | Twice in a month | Helping mother |
| 4. | Sampath | 15 days | Regular | Offer to street children | 10 – days | Helping mother |
| 5. | Sravya | 20 – days | 10-12 times | Nil | Once in a month | Grooming cleasing vessels etc. |
Answer:
“Health is wealth”. Everyone knows about this. If we maintain cleanliness of our hands and nails we can protect ourselves from epidemic diseases. If we keep our surrounding clean & neat we will protect ourselves from mosquitoes and other insects and be safe from dangerous diseases, If we are in healthy manner we will develop ourselves and our country will also be in prosperous.
That’s why Indian Government introduced Swatch Bharat Programme and protect our people from dangerous diseases like Dengue, Swineflu, Zika, etc.,
Finally everyone will be habituate for cleanliness.
8th Class Social Studies 9th Lesson Public Health and the Government InText Questions and Answers
![]()
Question 1.
What steps can be taken to prevent Malaria?
Answer:
- Necessary preventive measures should be taken from mosquito bites.
- We should use mosquito nets.
- Creams like Odomos.
- We should take care of drainage canals and small kuntas. Stagnated water should be dried.
- The smoke of Neem and Tulasi sticks should be spread in houses during evenings.
- Water tanks should be cleaned once in a month.
With these we can prevent malaria.
Question 2.
Why are children given food in the anganwadis? Do they get adequate food to eat in the anganwadis of your area? (Textbook Page No. 101)
Answer:
In Andhra Pradesh about 33% of children below 5 years of age were characterised as underweight. This is due to hunger and malnutrition. So the government decided to feed these children through Anganwadis.
We have two Anganwadi Kendras in our village. They provide nutrition in a certain quantities like Soya powder, Soya granules, Chips etc., to the children below 5 years.
Question 3.
What problems did Kiran face in the Government Hospital? How do you think could the hospital could work in a better manner? Discuss. (Textbook Page No. 103)
Answer:
- Kiran had to spend 3 hours standing in a queue for consultation.
- Again he spent two hours for blood test.
- He had to come on the second day for blood report by consultation.
- He took week days to go to his school regularly.
These hospitals can work in a proper manner. They can create more facilities to the patients. Seating arrangements can be provided. The test reports also can be issued on the same day.
![]()
Question 4.
What problems do we face in private hospitals? Discuss. (Textbook Page No. 103)
Answer:
Problems in private hospitals:
- We should pay more money here.
- Medicines also cost very high.
- Some may cause unnecessary tensions to the patient families.
Question 5.
Where do you go when you are ill? Are there any problems that you face? Write a paragraph based on your experience. (Textbook Page No. 103)
Answer:
Once I suffered from Typhoid. My father is a Railway employee. He joined me in Railway hospital. I stayed there for 10 days. Several blood tests were done. They treated me well. But they never disclose the results of any report. The patients were given a hospital uniform. I didn’t like wearing this uniform. On the whole I hate that atmosphere.
Question 6.
Why do you think do people in the rural areas go to untrained practitioners, even though they know that they are not properly trained? Keep in mind the following aspects in discussion- trained doctors do not work in villages; people have faith in injection; treat on credit; accepts payments like grains or chicken. (Textbook Page No. 104)
Answer:
Even though they are untrained practioners, they treat small diseases like fever, cold, cough etc., well. Some may have undergone RMP training, some may have worked under a trained doctor. Many of the people have faith on injections. They call it as ‘Soodi Mandu’. Many practitioners take the benefit of this belief. The fee can be paid in instalments or in barter system. These practitioners help the rural people by introducing them to specialists in the time of need and urgency. Due to all these reasons, the medical practitioners are treated as small gods in villages.
![]()
Question 7.
In India about one lakh women die each year of complications from pregnancy, it was observed that poor maternal health and nutritional status and inappropriate management of labour during delivery were responsible for many of the deaths of children. Do you think that 104 and 108 services have made a difference to the above situation? Discuss. (Textbook Page No. 109)
Answer:
I think 104 and 108 services have made a difference to the above situation.
Hiring an Ambulance from private is very expensive. But 108 reaches the patient within a short time, takes him/her to the nearest hospital by providing medical aid.
104 service creates awareness in the rural people. And they give medical assistance to needy people.
Question 8.
What should be available in every village as part of the public health system? (Textbook Page No. 104)
Answer:
Asha worker, nutrition, immunisation facilities, weighing machine etc., should be available in every village as part of the public health system.
Question 9.
List some public health centres or hospitals near your place. From your experience (or by visiting any one of them) find out the facilities provided and people who run the centre. (Textbook Page No. 104)
Answer:
1. Government General Hospital. 2. Primary Health Care Centre.
Facilities:
- Laboratory
- UltraSound Scanning.
- X-ray
- Pharmacy etc.
Government employees run the centre.
![]()
Question 10.
Mark sentences that highlight the relationship between public health and expectations from the government. (Textbook Page No. 106)
Answer:
“Self exercise” – The student should identify the sentences from this chapter.
Question 11.
Is the water you drink at school clean? (Textbook Page No. 101)
Answer:
Yes, the water at our school is clean. Our school is in Vijayawada Municipal Corporation. We have a water tank near our school. We get clean water from that tank. We clean our school tank once a month.
Question 12.
Private health services can mean many things. Explain with the help of some examples from your area. (Textbook Page No. 104)
Answer:
We live in Vijayawada. Many types of hospitals are presented here. Those are:
- Multispeciality Hospitals: The treatment is available for all kinds of diseases.
For e.g.: Ramesh Multispeciality Hospital. - Special Hospitals: The treatment here is related to some particular part/organ/body.
- Private Hospitals: Those are our family hospitals. They treat us for normal diseases. For e.g.: Dr. Prakash’s Hospital.
- Medical Centres: These are run by Medical Practitioners.
For e.g.: M.B. Sarada Medical Centre.
![]()
Question 13.
Write a short note on the health facilities available in your village or town. What are the problems that people of your neighborhood face when they go to government/ private hospitals? (Textbook Page No. 108)
Answer:
Ours is Tenali town. It is in Guntur district. Once here was only one doctor Dr. Sri- Buddhavarapu Krishna Rao. But we have many at present. The facilities in government hospital are a bit little than those in private hospitals.
More facilities are available in private hospitals. Here we have visited “Kanaka Durga Nursing Home”. The doctor is Buddhavarapu Satyanarayana, M.S. Ortho. This is in a single storeyed building. X-ray, blood test, medical shop – all facilities are available here. Sophisticated operation theatre is an asset to this hospital. The doctor is dedicated and service oriented. The premises is very neat and clean. The consultation fees is also in the reach of middle class ‘people. They render free service to the poor people.
The patients who approach government hospital are losing their valuable time. Corruption is also a curse on this department. The people who approach private hospitals are losing money.
Question 14.
Use the following questions to do a small survey on immunisation of children in your area (in five households having children under 2 years).
a. Do you have an immunization card for the child?
b. Did your child get a vaccine on the left arm that has left a mark? (Look for a scar if you can.)
c. Did your child get vaccination on the buttock?
d. Did your child get polio drops? How many times?
e. Did your child get a vaccination on the thigh at 9 months along with a spoon of medicine?
f. Did your child get any vaccination at 18 months of age (if the child is older than this)? Did she/ he get any medicine to drink also?
For each question, answer with Yes / No; No. of doses (where applicable); DK (for don’t know)/ NA (not applicable; for example, question ‘V will not be applicable if the baby is 1 year old). Discuss your results. (Textbook Page No. 108)
Answer:
1) Family of Sai Kanaka Durga:
a) Yes b) Yes c) Yes d) Yes, 4 times e) Yes f) Yes – Deepa – 4 years – Yes.
2) Family of Krishnarao & Durgamba:
a) Yes b) Yes c) Yes d) Yes, 4 times e) Yes f) Yes – Babji – Age : 1 year Yes.
3) Family of Madhavarao & Rajya Lakshmi:
a) Yes b) Yes c) Yes d) Yes 3 times e) Not applicable – Bobby – 6 months – Yes.
4) Rambabu & Subbha Lakshmi Family:
a) Yes b) Yes c) Yes d) Yes, 2 times e) Yes f) Yes
5) Hanumantharao & Kameswari’s family:
a) Yes b) Yes c) Yes d) Yes, 5 times e) Yes f) Yes
After my sincere observation I came to a conclusion that all parents are caring for their children’s health.
![]()
Question 15.
The Aarogyasri scheme was started as a medical insurance scheme to white card holding families, for treatment that requires hospitalisation. The scheme covers very large number of illnesses and includes many private hospitals as providers. Discuss with some people in your neighbourhood and write a short note on the effectiveness of the scheme. (Textbook Page No. 109)
Answer:
‘Aarogyasri’ scheme is really helpful to the poor people. Once my father joined in a private hospital. Then I noticed that many people had undergone free treatment. But at present many diseases are outlisted. So this is not useful to all in all times.
Question 16.
In your opinion, what is one most important improvement that should be made for the mid-day meal being served at your school? (Textbook Page No. 109)
Answer:
The quality of rice should be changed. Better quality should be maintained.
Question 17.
What are the reasons for doctors not accepting rural posting? (Textbook Page No. 101)
Answer:
- Rural backwardness.
- Lack of modern facilities.
- More financial benefits are not available.
- Lack of medical facilities.
- Interest in private practice. These are the reasons behind it.
![]()
Question 18.
Why did Saritha have to spend so much money? Give reasons. (Textbook Page No. 103)
Answer:
Soon after Saritha got viral fever, her father took her to a private hospital and got her tested.
The doctor recommended a number of blood tests and a chest X-ray. He also prescribed several medicines. She had to spend money for all these tests and medicines to get well soon. She became healthy within 3 days and went to school.
Question 19.
Most of the medical facilities in both the private and public sectors are located in urban areas. A study conducted during 2003 based on a sample survey in selected areas found that most of the qualified private doctors (79 per cent) were in the urban areas. The actual availability of doctors in rural areas, though officially posted in these areas, may be negligible, given the widespread prevalence of absenteeism. Discuss the reasons for this situation. Talk to people in your area about this problem and in what ways this be can tackled. (Textbook Page No. 108)
Answer:
Reasons:
- Medical education is very costly.
- The persons, who incur expenditure on studies, try to get back the same.
- There is a rapid growth in urbanization.
- All the facilities for treatment are cheap in cities and towns.
Transport facilities, housing facilities and drinking water facilities are nominal in the rural areas.
So these conditions arise.
This can be tackled by creating social awarness in the medical students. “Villages and villagers are the backbone of the nation”. This concept should be injected into their minds.
