AP State Syllabus AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures Ex 9.2 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 9th Lesson Area of Plane Figures Exercise 9.2
![]()
Question 1.
A rectangular acrylic sheet is 36 cm by 25 cm. From it, 56 circular buttons, each of diameter 3.5 cm have been cut out. Find the area of the remaining sheet.
Solution:
The dimensions of a rectangular acrylic sheet = 36 cm × 25 cm.
∴ Its area = l × b
= 36 × 25 = 900 sq.cm
The diameter of a circular button = 3.5 cm
radius = r = \(\frac{d}{2}=\frac{3.5}{2}\) = 1.75 cm.
∴ Area of each button = πr2
= \(\frac{22}{7}\) × (1.75)2
= \(\frac{22}{7}\) × 1.75 × 1.75
= 9.625 sq.cm.
The area of 56 such buttons = 56 × 9.625 = 539 sq.cm.
∴ The area of remaining sheet
= Area of a rectangular sheet – Area of 56 buttons
= 900 – 539
= 361 sq.cm
![]()
Question 2.
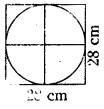
Find the area of a circle inscribed in a square of side 28 cm.
[Hint. Diameter of the circle is equal to the side of the square]
Solution:
Diameter of a circle = d = side of a square = 28 cm.
∴ d = 28 cm
⇒ r = \(\frac{d}{2}=\frac{28}{2}\) = 14 cm
∴ Area of a circle = \(\frac{22}{7}\) × 14 × 14
= 22 × 28
= 616 sq.cm.
Question 3.
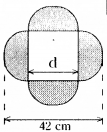
Find the area of the shaded region in each of the following figures.
[Hint:d + \(\frac{d}{2}\) + d/2 = 42]
d = 21
∴ side of the square 21 cm
i)
Solution:

∴ Side of a square, d = 21 cm.
Radius of a semicircle = r = \(\frac{\mathrm{d}}{2}=\frac{21}{2}\) = 10.5 cm
∴ Area of a semi-circle = \(\frac{\pi r^{2}}{2}\)
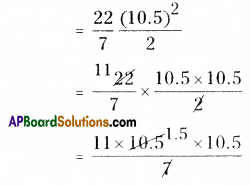
= 11 × 1.5 × 10.5
= 173.250 sq.cm.
∴ Area of 4 shaded semi-circles
= 4 × Area of each semi-circle
= 4 × 173.25 = 693 sq.cm.
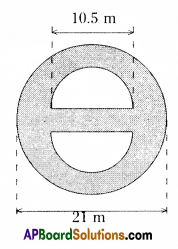
Diameter of a big circle = 21 m

Diameter of a semicircle = 10.5 m.
Radius = \(\frac{10.5}{2}\) = 5.25 m.
∴ Area of semi-circle = \(\frac{\pi r^{2}}{2}\)
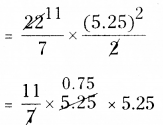
= 11 × 0.75 × 5.25
= 43.3125 sq.m.
Area of two semicircles
= 2 × 43.3125 = 86.6250 sq.m.
∴ Area of shaded region
= Area of big circle – Area of 2 semicircles
= 346.5 – 86.6250
= 259.8750 sq.m.
![]()
Question 4.
The adjacent figure consists of four small semi-circles of equal radii and two big semi-circles of equal radii (each 42 cm). Find the area of the shaded region
Solution:
Diameter of a bigger semi circle d = 42 cm
Radius, r = \(\frac { 42 }{ 2 }\) = 21 cm
Area of a bigger semi circle = \(\frac{\pi r^{2}}{2}\)
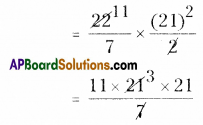
= 11 × 3 × 21
= 693 sq.cm
∴ Area of the shaded region
= Area of two bigger semi circles – Area of two smaller semi circles + Area of two smaller semi circles
= Area of two bigger semi circles
= 2 × Area of bigger semi circles
= 2 × 693 = 1386 sq.cm.
Question 5.
The adjacent figure consists of four half circles and two quarter circles.
If OA=OB=OC=OD= 14cm. Find the area of the shaded region.
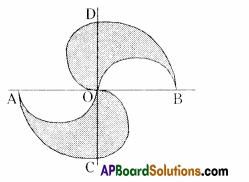
Solution:
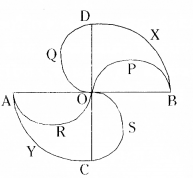
OA = OB = OC = OD = 14CM
Radius of \(\frac { 1 }{ 4 }\) of circle BXD, r = 14cm
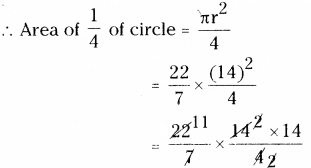
= 154 sq.cm.
∴ Area of the quarter circle AYC
= 154 sq.cm
.’. Area of the shaded region = Area of quarter circle BXD – Area of semi circle OPB + Area of semi circle OQD + Area of quarter circle AYC – Area of semi circle ARO + Area of semi circle OSC
= Area of quarter circle BXD + Area of quarter circle AYC
= 154 + 154
= 308 sq.cm.
![]()
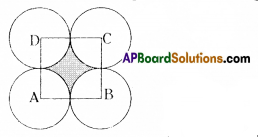
Question 6.
In adjacent figure A, B, C and D are centres of equal circles which touch externally is pairs and ABCD is a square of side 7 cm. Find the area of the shaded region.
Solution:
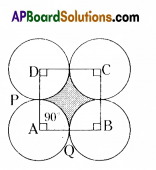
Side of a square,
AB = BC = CD = DA = 7 cm
Area of a square = s × s
= 7 × 7 = 49 sq.cm.
From the above figure,
Radius of a circle, r = \(\frac{\text { Side of a square }}{2}\)
= \(\frac{7}{2}\) = 3.5
Areas of 4 equal sectors are equal.
Angle of a sector APQ, x = 90°
Radius, r = 3.5 cm
Area of sector APQ

= 5.5 × 0.5 × 3.5
= 9.625 sq.cm.
Total area of 4 equal sectors = 4 × 9.625 = 38.5 sq.cm.
∴ Area of shaded region = Area of square ABCD – Area of 4 equal sectors
= 49 – 38.5
= 10.5 sq.cm.
![]()
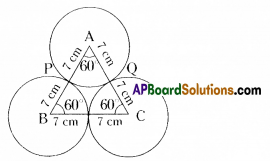
Question 7.
The area of an equilateral triangle is 49√ cm2. Taking each angular point as centre, a circle is described with radius equal to half the length of the side of the triangle as shown in the figure. Find the area of the portion in the triangle not included in the circles.
Solution:
From the given figure,
Δ ABC is an equilateral triangle.
∴ Area of an equilateral triangle
= 49√3 sq.em (given)
3 equal circles (whose radii are equal) are touch externally.
Each angle of a sector in the circle = 60°,
Radius r = 7 cm.
∴ The areas of 3 sectors are equal.
∴ Area of a sector APQ
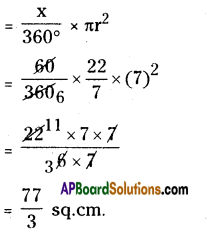
∴ The area of 3 sectors
= 3 × \(\frac { 77 }{ 3 }\) = 77 sq. cm
∴ The area of the portion in the triangle not included in the circles
= area of ΔABC — area of 3 equal sectors
=49√3 – 77
=49 × 1.7321 – 77 (∵√3 = 1.7321)
= 84.8729 – 77
= 7.8729 sq.cm.
Question 8.
(i) Four equal circles, each of radius ‘a’ touch one another. Find the area between them.
(ii) Four equal circles are described about the four corners of a square so that each circle
touches two of the others. Find the area of the space enclosed between the circumferences
of the circles, each side of the square measuring 14 cm.
Solution:
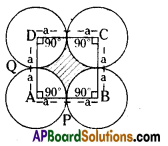
The side of a square ABCD
AB = BC = CD = DA = a + a = 2a units.
∴ Area of a square = s × s
= 2a × 2a = 4a2 sq.units.
4 equal sectors are there.
In each sector,
The angle of a sector APQ, x = 90°
Radius, r = a units
Area of each sector APQ

∴ Area of 4 equal sectors
= 4 × \(\frac{\pi \mathrm{a}^{2}}{4}\) = πa2 sq. units
= 2a × 2a = 4a2 sq.units. 4 equal sectors are there.
∴ The area between the circles
= Area of square sectors
= 4a2 – πa2
= a2 (4 – π) sq. units
= a2 (4 – \(\frac { 22 }{ 7 }\) ) = \(\frac{6 a^{2}}{7}\) sq. units
![]()
Question 9.
From a piece of cardbord, in the shape ofa trapezium ABCD, and AB||CD and ∠BCD = 90°,= quarter circle is removed. Given AB = BC = 3.5 cm and DE =2 cm. Calcualte the area of the remaining piece of the cardboard. (Take π to be \(\frac{22}{7}\) )
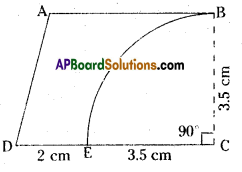
Solution:
ABCD is a trapezium
AB || CD and ZBCD = 90°
AB = BC = 3.5 cm; DE = 2 cm.
Area of a trapezium ABCD :
Length of parallel sides, AB = 3.5 cm
CD = DE + EC
= 2 + 3.5 = 5.5 cm.
Distance between parallel sides,
BC = 3.5 cm.
∴ Area of a trapezium
= \(\frac { 1 }{ 2 }\) h (a + b)
= \(\frac { 1 }{ 2 }\) × BC (AB + CD)
= \(\frac { 1 }{ 2 }\) × 3.5 (3.5 + 5.5)
= \(\frac { 1 }{ 2 }\) × 3.5 × 9
= 3.5 × 4.5
= 15.75 sq.cm.
Area of quarter circle EBC :
Radius, r = 3.5 cm
∴ Area of quarter circle
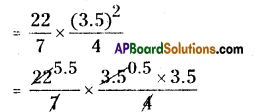
= 5.5 × 0.5 × 3.5
= 9.625 sq.cm.
Area of the remaining piece of card board = Area of a trapezium – \(\frac { 1 }{ 2 }\) th of area of a circle
= 15.75 – 9.625
= 6.125 sq.cm.
Question 10.
A horse is placed for grazing inside a rectangular field 70 m by 52 m and is tethered to one corner by a rope 21 m long. How much area can it graze?
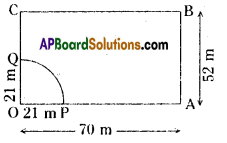
Solution:
From the above figure,
The sector represents the grazing area of a horse.
The angle of a sector OPQ, x = 90°
Radius of a sector OPQ, r = 21 m .
∴ Area of a sector
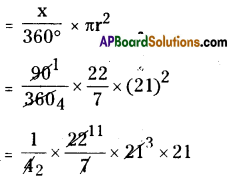
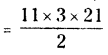
= 346.5 sq.m.
∴ The area of grazing = 346.5 sq.m.
