AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers InText Questions and Answers.
8th Class Maths 15th Lesson Playing with Numbers InText Questions and Answers
Do this
Question 1.
Write the place value of numbers underlined. (Pg. No: 312)
i) 29879 ii) 10344 iii) 98725
Answer:
i) 29879
Place value of 8 = 8 × 100 = 800
Place value of 2 = 2 × 10,000 = 20,000
ii) 10344
Place value of 4 = 4 × 1 = 4
Place value of 3 = 3 × 100 = 300
iii) 98725
Place value of 5 = 5 × 1 = 5
Place value of 8 = 8 × 1000 = 8,000
![]()
Question 2.
Write the following numbers in expanded form, (Pg. No: 313)
i) 65 ii) 74 iii) 153 iv) 612
Answer:
Number Expanded form
i) 65 = 60 + 5 = (6 × 101) + (5 × 100)
ii) 74 = 70 + 4 = (7 × 101) + (4 × 100)
iii) 153 = 100 + 50 + 3 = (1 × 102) + (5 × 101) + (3 × 100)
iv) 612 = 600 + 10 + 2 = (6 × 102) + (1 × 101) + (2 × 100)
Question 3.
Write the following in standard notation. (Pg. No: 313)
i) 10 × 9 + 4 ii) 100 × 7 + 10 × 4 + 3
Answer:
Expanded form General form
i) 10 × 9 + 4 = 90 + 4 = 94
ii) 100 × 7 + 10 × 4 + 3 = 700 + 40 + 3 = 743
Question 4.
Fill in the blanks. (Pg. No: 313)
Answer:
i) 100 × 3 + 10 × ——— + 7 = 357 (5)
ii) 100 × 4 + 10 × 5 + 1 = ——— (451)
iii) 100 × ——— + 10 × 3 + 7 = 737 (7)
iv) 100 × ——— + 10 × q + r = \(\overline{\mathrm{pqr}}\) (p)
v) 100 × x + 10 × y + z = ——— (\(\overline{\mathrm{xyz}}\))
Do you know?
Question 5.
The number 8281807978777675747372717069686766656463626160595857565554535251504948474645444342414039383736353433323130292827262524232221201918 1716151413121110987654321 is written by starting at 82 and writing backwards to 1 and see that it is a prime number. (Pg. No: 313)
Answer:
No.of digits in the given number are 155.
![]()
Question 6.
Write all the factors of the following numbers. (Pg. No: 314)
a) 24 b) 15 c) 21 d) 27 e) 12 f) 20 g) 18 h) 23 i) 36
Answer:
a) Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
b) Factors of 15 = 1, 3, 5, 15
c) Factors of 21 = 1, 3, 7, 21
d) Factors of 27 = 1, 3, 9, 27
e) Factors of 12 = 1, 2, 3, 4, 6, 12
f) Factors of 20 = 1, 2, 4, 5, 10, 20
g) Factors of 18 = 1, 2, 3, 6, 9, 18
h) Factors of 23 = 1, 23
i) Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Question 7.
Write first five multiples of given numbers (Pg. No: 314)
a) 5 b) 8 c) 9
Answer:
a) Multiples of 5 = 5, 10, 15, 20, 25
b) Multiples of 8 = 8, 16, 24, 32, 40
c) Multiples of 9 = 9, 18, 27, 36, 45
Question 8.
Factorize the following numbers into prime factors. (Pg. No: 314)
a) 72 b) 158 c) 243
Answer:
a) 72 = 2 × 2 × 2 × 3 × 3
b) 158 = 2 × 7 × 9
c) 243 = 7 × 7 × 7
Question 9.
Check whether the following given numbers are divisible by 10 or not. (Pg. No: 315)
a) 3860 b) 234 c) 1200 d) 103 e) 10 + 280 + 20
Answer:
a) 3860, c) 1200, d) 103, e) 10 + 280 + 20 are divisible by ’10’.
[∵ the units digit of above numbers is ‘0’]
b) 234, is not divisible by 10.
[∵ its unit digit is 4]
Question 10.
Check whether the given numbers are divisible by 10 or not. (Pg. No: 315)
a) 1010 b) 210 c) 103 + 101
Answer:
a) 1010 = 10000000000
b) 210 = 1024
c) 103 + 101 = 1000 + 10 = 1010
∴ a) 1010, c) 103 + 101 are divisible by ’10’.
[∵ Their units digits are ‘0’.]
b) 1024 is not divisible by 10.
[∵ Its units digit is 4.]
![]()
Question 11.
Check whether the given numbers are divisible by 5 or not (Pg. No: 315)
a) 205 b) 4560 c) 402 d) 105 e) 235785
Answer:
a) 205, b) 4560, d) 105, e) 235785 are divisible by 5.
[∵ The units digit of the above numbers are either 0 (or) 5.]
c) 402 is not divisible by 5.
[∵ Its units digit is 2.]
Question 12.
Check whether the given numbers which are divisible by 3 or 9 or by both, (Pg. No: 318)
a) 3663 b) 186 c) 342 d) 18871 e) 120 f) 3789 g) 4542 h) 5779782
Answer:
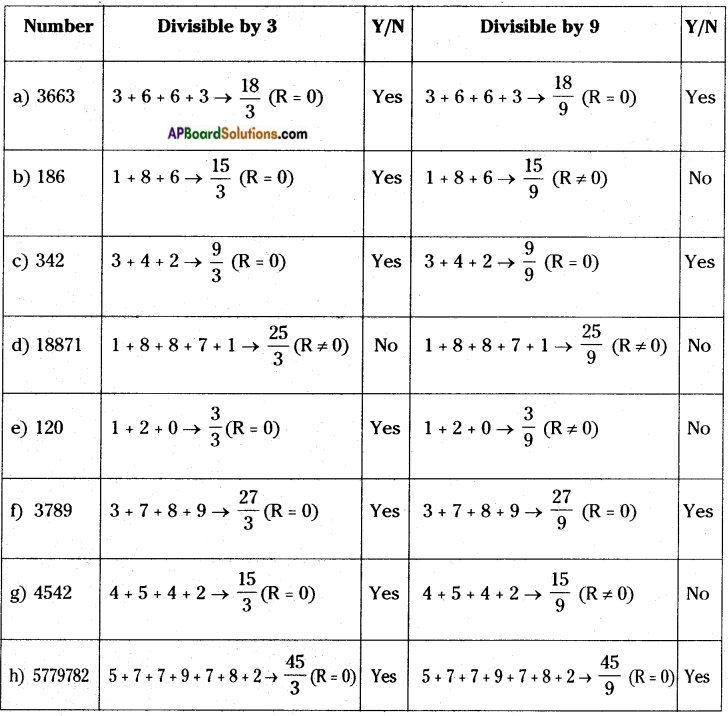
![]()
Question 13.
Check whether the given numbers are divisible by 6 or not. (Pg. No: 320)
a) 1632 b) 456 c) 1008 d) 789 e) 369 f) 258
Answer:
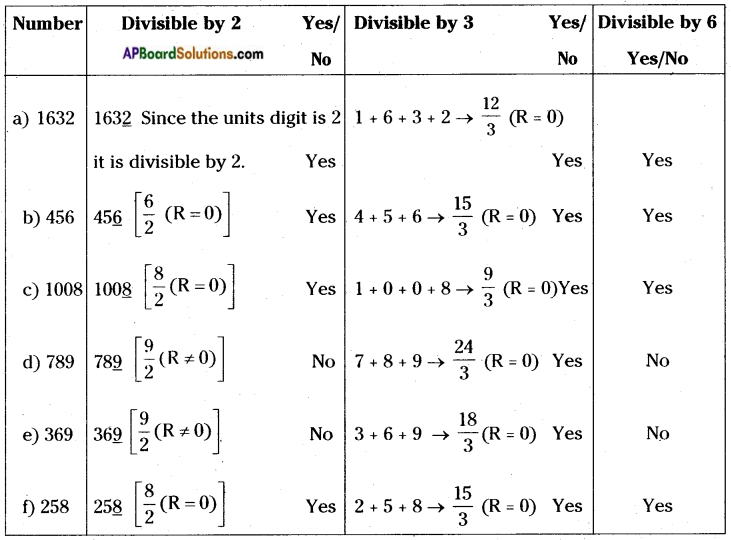
Question 14.
Check whether the given numbers are divisible by 6 or not. (Pg. No: 320)
a) 458 + 676 b) 63 c) 62 + 63 d) 22 × 32
Answer:

![]()
Question 15.
Can you arrange the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 in an order so that the number formed by first two digits is divisible by 2, the number formed by first three digits is divisible by 3, the number formed by first four digits is divisible by 4 and so on upto nine digits?
Solution: The order 123654987 looks promising check and verify. (Pg. No : 320)
Answer:

∴ This number can’t continue upto ‘9’.
→ 123654987

∴ The given number 123654987 is not divisible by all the numbers like 2, 3, 4, 5,……… 9.
Question 16.
Check whether the given numbers are divisible by 4 or 8 or by both 4 and 8.
a) 464 b) 782 c) 3688 d) 100 e) 1000 f) 387856 g)44 h) 83 (Pg. No: 321)
Answer:
If a number is divisible by 4 then the last two digits of the number must be divisible by 4.
If the last 3 digits of a number is divisible by 8 then it is divisible by 8.
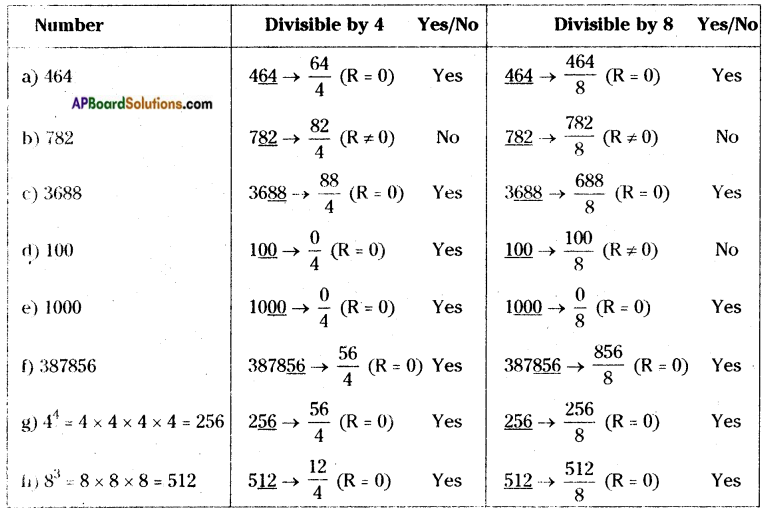
![]()
Question 17.
Check whether the given numbers are divisible by 7. (Pg. No: 322)
a) 322 b) 588 c) 952 d) 553 e) 448
Answer:

All the given numbers are divisible by ‘7’.
Question 18.
Check whether the given numbers are divisible by 11. (Pg. No: 323)
i) 4867216 ii) 12221 iii) 100001
Answer:
If the difference between the sum of digits of odd places and even places is divisible by 11, then entire number is divisible by 11.

Question 19.
Take different pairs of numbers and check the above four rules. (Pg. No: 325)
Answer:
a) Consider a factor of 36, say 9.
Factors of 9 are 1,3,9.
∴ 36 is divisible by 1, 3, 9.
∴ 36 is also divisible by all the factors of 9.
b) Let us consider a number 60. It is divisible by 5 and 6. It is also divisible by 5 x 6 = 30 Where 5, 6 are co-primes.
c) Take two numbers 25, 30. These numbers are both divisible by 5.
The number 25 + 30 = 55 is also divisible by 5.
d) Take two numbers 36, 54. These numbers are both divisible by 9.
Their difference i.e., 54 – 36 = 18 is also divisible by 9.
Question 20.
144 is divisible by 12. Is it divisible by the factors of 12? Verify. (Pg. No : 325)
Answer:
Factors of 12 = 1, 2, 3, 4, 6, 12.
If 12 is a factor of 144 then 144 is divisible by all the factors of 12.
Question 21.
Check whether 23 + 24 + 25 is divisible by 2. Explain. (Pg. No : 325)
Answer:
23 + 24 + 25 = 8 + 16 + 32 = 56 is an even.
∴ 56 is divisible by 2.
![]()
Question 22.
Check whether 33 – 32 is divisible by 3. Explain (Pg. No : 325)
Answer:
33 – 32 = 27 – 9 = 18 → 1 + 8 = 9 ⇒ \(\frac{9}{3}\) (R = 0)
∴ It is divisible by ‘3’.
Question 23.
Check the result if the numbers chosen were (Pg. No : 328)
i) 37 ii) 60 iii) 18 iv) 89
Answer:
i) If the digits are interchanged in 37 then it becomes as 73.
∴ 37 + 73 = 110 → \(\frac{110}{11}\) (R = 0)
It is divisible by ’11’.

Question 24.
In a cricket team there are 11 players. The selection board purchased 10x + y T-shirts to players. They again purchased ‘10y + x’ T-shirts and total T-shirts were distributed to players equally. How many T-shirts will be left over after they distributed equally to 11 players ? How many each one will get? (Pg. No : 328)
Answer:
No.of players in the team = 11
No.of T- shirts are purchased at first = 10x + y
No. of T – shirts are purchased for the 2nd time = 10y + x
Sum of the T – shirts = (10x + y) + (10y + x)
= 11x + 11y = ll(x + y)
∴ 11(x + y) T – shirts are distributed among 11 players then each will get ll(x + y)
\(\frac{11(x + y)}{11}\) = x + y
Remaining T – shirts = Purchased T – shirts – 11 (No.of T-shirts got by each)
= 11(x + y) – 11(x + y)
= 0
![]()
Question 25.
In a basket there are ‘10a + b’ fruits (a ≠ 0 and a > b). Among them ‘10b + a’ fruits are rotten. The remaining fruits distributed to 9 persons equally. How many fruits are left over after equal distribution? How many fruits would each child get? (Pg. No: 328)
Answer:
No. of fruits in a basket = 10a + b
No. of fruits are rotten = 10b + a
Remaining fruits to be distributed = (10a + b) – (10b + a)
= 10a + b – 10b – a
= 9a – 9b = 9(a – b)
∴ 9(a – b) fruits are distributed among ‘9’ Children
then each will get = 9(a – b) ÷ 9 = \(\frac{9(a – b)}{9}\) = (a – b)
No. of fruits left over after distribution
= Total no. of fruits distributed – No.of fruits got by each
= 9(a – b) – 9(a – b) = 0
Question 26.
Check in the above activity with the following numbers. (Pg. No: 329)
i) 657 ii) 473 iii) 167 iv) 135
Answer:
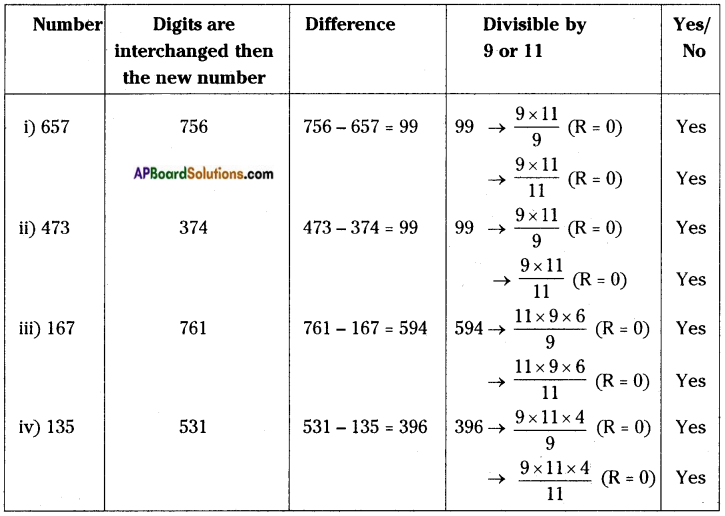
Question 27.
If 21358AB is divisible by 99, find die values of A and B. (Pg. No: 331)
Answer:
If 21358AB is divisible by 99, then it is divisible by 9 and 11.
If 21358AB is divisible by 9 then the sum of the digits is divisible by 9.
2 + 1 + 3 + 5 + 8 + A + B = 9 × 3 say
⇒ 19 + A + B = 27
⇒ A + B = 27-19 = 8
A + B = 8 …… (1)
If 21358AB is divisible by ‘ll’ then the difference of sum of even and odd digits will be divisible by’ll’.
2 1 3 5 8 A B
∴ (2 + 3 + 8 + B) – (1 + 5 + A) = 11 × 1 say
⇒ 13 + B – 6 – A = 11
⇒ B – A = 11 – 7 = 4 ……. (2)
From (1) & (2) A = 2, B = 6
∴ The required number is 21358AB = 2135826 which is divisible by 99.
![]()
Question 28.
Find the values of A and B of file number 4AB8 (A, B are digits) which is divisible by 2, 3, 4, 6, 8 and 9. (Pg. No: 331)
Answer:
Given number is 4AB8.
4AB8 → \(\frac{8}{2}\) (R = 0) so, it is divisible by ‘2’.
4AB8 → If it is divisible by ‘3’, sum of all the digits should be a multiple of ‘3’. .
∴ 4 + A + B + 8 = 3 or 6 or 9 or 12 or 15 …….

4AB8 → If it is divisible by 9, sum of all the digits should be a multiple of ‘9’.
∴ 4 + A + B + 8 = 9 or 18 or 27 or 36
⇒ A + B + 12 = 9 ∣18∣ 27∣ 36 ……. (3)
From (1) & (3)
A + B + 12 = 9 or 18 say
If A + B + 12 = 9
A + B = 9 – 12 = -3
It is impossible
If A + B + 12 = 18
A + B = 18 – 12 = 6
∴ A + B = 6
If A = 4 & B = 2
4AB8 = 4428
4AB8 → 4428 → \(\frac{428}{8}\) (R ≠ 0)
∴ A = 4 & B = 2 are not possible.
If A = 2& B = 4
4AB8 → 4248 → \(\frac{248}{8}\) (R = 0)
∴ A = 2 and B = 4
![]()
Question 29.
By using the above method check whether 7810364 is divisible by 4 or not. (Pg. No: 333)
Answer:
Given number = 7810364
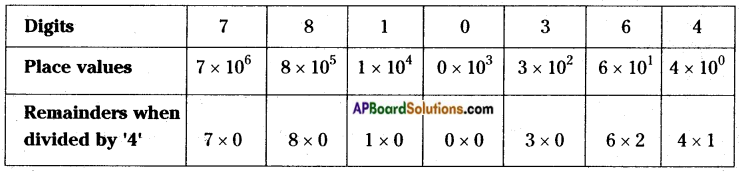
Sum of product of place values and remainders of place values = 0 + 0 + 0 + 0 + 0 + 12 + 4
→ \(\frac{16}{4}\) (R = 0)
∴ 7810364 is divisible by ‘4’.
Question 30.
By using the above method check whether 963451 is divisible by 6 or not. (Pg. No: 333)
Answer:
The given number = 963451
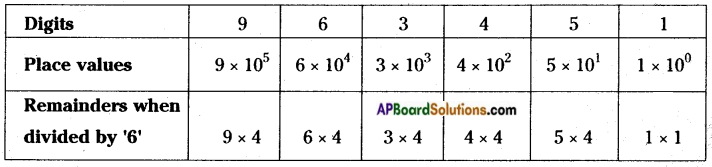
Sum of product of place values and remainders of place values
= 36 + 24 + 12 + 16 + 20 + 1 → \(\frac{109}{6}\) (R ≠ 0)
∴ 963451 is not divisible by ‘6’.
Try these
Question 1.
In the division 56 Z ÷ 10 leaves remainder 6, what might be the value of Z. (Pg. No: 315)
Answer:
Let 56Z, Z = 0, 1,2, 3, 4, ….. , 9 say.
To obtain remainder ‘6’ when divided by 10, Z = 6
\(\frac{566}{10}\) = \(\frac{560+6}{10}\)
Remainder is 6.
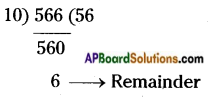
∴ Z = 6
![]()
Question 2.
If 4B ÷ 5 leaves remainder 1, what might be the value of B? (Pg. No : 316)
Answer:
If 4B is divided by 5 then remainder should be ‘1’,
∴ B = {0, 1, 2, ….. , 9}
i.e., 40, 41, 42, …… , 49
From the above numbers we have to take 41 and 46.
41 and 46 are divided by 5 and leaves the remainder 1.
∴ B = {1, 6}
Question 3.
If 76C ÷ 5 leaves remainder 2, what might be the value of C? (Pg. No: 316)
Answer:
To get remainder 2, when 76C is divided by 5 take C = {0, 1,……, 9}.
If C = 2, 7 then
76C = 762 or 767 are divided by 5 leaves the remainder 2.
Question 4.
“If a number is divisible by 10, it is also divisible by 5.” Is the statement true? Give reasons. (Pg. No : 316)
Answer:
The given statement is true.
∵ When a number is divisible by ’10’, then its units digit should be ‘0’.
Similarly the units digit of a number is 5 or 0, then it is divisible by 5.
∴ The number which is divisible by 10 is also divisible by 5.
Question 5.
“If a number is divisible by 5, it is also divisible by 10.” Is the statement is true or false? Give reasons. (Pg. No : 316)
Answer:
The given statement is false.
∵ If a number is divisible by 5, then its units digit must be ‘5’ or ‘0’. But in case of 10, it . must be ‘0’ only.
∴ The number which is divisible by ‘5’ is need not be divisible by ’10’.
Question 6.
Check whether the given numbers are divisible by 4 or 8 or by both 4 and 8. (Pg. No : 321)
a) 42 × 82 b) 103 c) 105 + 104 + 103 d) 43 + 42 + 41 – 22
Answer:
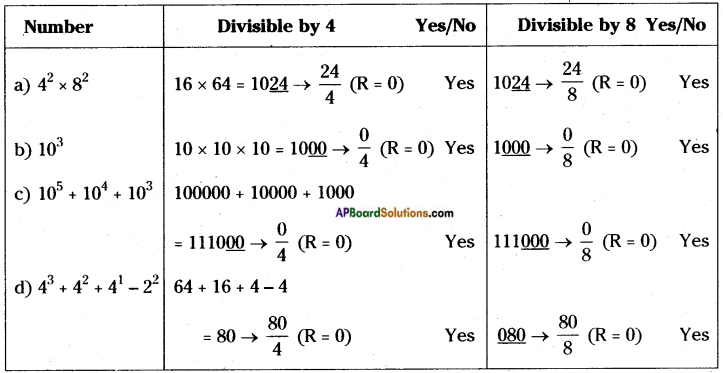
![]()
Question 7.
Take a four digit general number, make the divisibility rule for ‘7’. (Pg. No : 322)
Answer:
Let the 4 – digited number be ‘abcd’ say.
The remainders when divided by ‘7’,

∴ If (6a + 2b + 3c + d) is divisible by 7 then the 4 – digited number be divisible by ‘7’.
Question 8.
Check your rule with the number 3192 which is a multiple of 7. (Pg. No : 322)
Answer:
The given number is 3192
⇒ a = 3, b = 1, c = 9, d = 2
6a + 2b + 3c + d = 6 × 3 + 2 × l + 3 × 9 + 2.
= 18 + 2 + 27 + 2
= 49 → \(\frac{49}{7}\) (R = 0)
∴ 3192 is divisible by 7’according to my law.
Question 9.
1) Verify whether 789789 is divisible by 11 or not. (Pg. No: 323)
2) Verify whether 348348348348 is divisible by 11 or not.
3) Take an even palindrome i.e. 135531 check whether this number is divisible by 11 or not.
4) Verify whether 1234321 is divisible by 11 or not.
Answer:

![]()
Question 10.
Check whether 1576 × 1577 × 1578 is divisible by 3 or not. (Pg. No : 325)
Answer:
The given number is 1576 × 1577 × 1578.
The product of any 3 consecutive numbers is divisible by ‘3’.
Ex : 4 × 5 × 6 = 120 → \(\frac{120}{3}\) (R = 0)
∴ 1576 × 1577 × 1578 is divisible by ’3’.
Question 11.
Check the above method applicable for the divisibility of 11 by taking 10-digit number. (Pg. No : 326)
Answer:
The largest 10 – digited number = 9,99,99,99,999
D C B A
∴ 9/999/999/999
⇒ B + D = 9 + 999 = 1008
A + C = 999 + 999 = 1998
∴ (A + C) – (B + D) = 990 → \(\frac{990}{11}\) (R = 0)
∴ The largest 10 – digited number should be divisible by 11 according to this method.
Question 12.
Take a three digit number and make the new numbers by replacing its digits as (ABC, BCA, CAB). Now add these three numbers. For what numbers the sum of these three numbers is divisible? (Pg. No : 329)
Answer:

Question 13.
If YE × ME = TTT find the numerical value of Y + E + M + T.
[Hint: TTT = 100T + 10T + T = T(111) = T(37 × 3)] (Pg. No: 332)
Answer:
TTT = 100T + 10T + T
= T(111)
= T(37 × 3)
∴ YE × ME = T(37 × 3)
∴ T ={1, 2, 3, ….., 9}
But T = {3, 6, 9} are multiples of 3.
T(37 × 3) = 3(111), 6(111), 9(111) are divisible by 3.
∴ YE × ME = 333∣666∣999
YE × ME = 999 = 27 × 37
∴ Y = 2, M = 3, E = 7, T = 3
∴ Y + E + M + T = 2 + 3 + 7 + 3 = 15
![]()
Question 14.
If cost of 88 articles is A733B, find the values of A and B. (Pg. No: 334)
Answer:
If A733B is divisible by 88 then it is divisible by 8 × 11.
Divisibility of 11:
⇒ A733B → (A + 3 + B) – (7 + 3) = 0
⇒ A + B = 7 ……. (1)
Divisibility of 8:
⇒ A733B ⇒ \(\frac{33B}{8}\)
∴ \(\frac{336}{8}\) (R = 0) (If B = 6 then it is divisible by 8)
∴ B = 6 ……. (2)
From (1), (2)
∴ A = 1, B = 6
Question 15.
Check whether 456456456456 is divisible by 7, 11 and 13. (Pg. No: 334)
Answer:
∴ The given number = 456456456456
456456456456 = 456 (1001001001)
= 456 × (7 × 11 × 13) × (1000001)
∴ 456456456456 is divisible by 7, 11 and 13.
Think, Discuss and Write
Question 1.
Find the digit in the units place of a number if it is divided by 5 and 2 leaves the remainders 3 and 1 respectively. (Pg. No: 316)
Answer:
If a number is divided by 5 and 2 leaves the remainders 3 and 1 respectively, then its units digit be 3.
Ex: \(\frac{13}{5}\) ⇒ (R = 3), \(\frac{13}{2}\) ⇒ (R = 1)
\(\frac{23}{5}\) ⇒ (R = 3), \(\frac{23}{2}\) ⇒ (R = 1)
∴ The unit’s digit of a required number be 3.
![]()
Question 2.
Take a two digit number reverse the digits and get another number. Subtract smaller number from bigger number. Is the difference of those two numbers is always divisible by 9? (Pg. No : 328)
Answer:
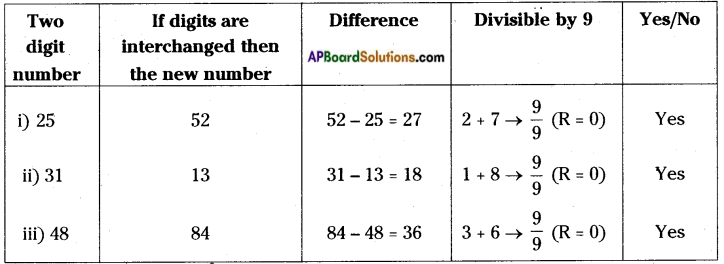
Question 3.
1) Can we conclude 102n – 1 is divisible by both 9 and 11? Explain. (Pg. No: 333)
2) Is 102n+1 – 1 is divisible by 11 or not? Explain.
Answer:

![]()
Question 4.
Verify a5 + b5 is divisible by (a + b) by taking different natural numbers for ‘a’ and ‘b’. (Pg. No : 334)
Answer:

∴ a5 + b5 is divisible by (a + b).
∴ (a5 + b5) is divisible by (a + b) for all the values of a, b.
Question 5.
Can we conclude (a2n+1 + b2n+1) is divisible by (a + b)? (Pg. No : 334)
Answer:

a2n+1 + b2n+1 is divisible by (a + b) for all the values of ‘n’.
