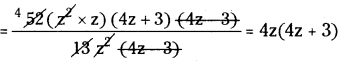AP Board 8th Class Maths Solutions Chapter 12 Factorisation Ex 12.3

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 12 Factorisation Ex 12.3 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 12th Lesson Factorisation Exercise 12.3

Question 1.
Carry out the following divisions
(i) 48a³ by 6a
(ii) 14x³ by 42x³
(iii) 72a³b⁴c⁵ by 8ab²c³
(iv) 11xy²z³ by 55xyz
(v) -54l⁴m³n² by 9l²m²n²
Solution:
(i) 48a³ by 6a
48a³ ÷ 6a
= \(\frac{6 \times 8 \times a \times a^{2}}{6 \times a}\)
= 8a²

(ii) 14x³ by 42x³
= 14x³ ÷ 42x³

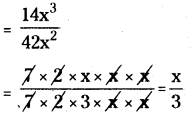
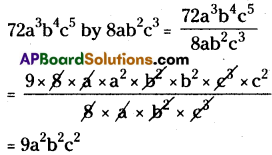
(iii) 72a³b⁴c⁵ by 8ab²c³

(iv) 11xy²z³ by 55xyz
11xy²z³ ÷ 55xyz

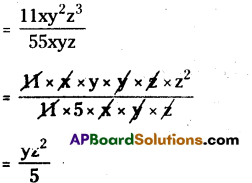
(v) -54l⁴m³n² by 9l²m²n²
-54l⁴m³n² ÷ 9l²m²n²

= -6l²m

Question 2.
Divide the given polynomial by the given monomial
(i) (3x² – 2x) ÷ x
(ii) (5a³b – 7ab³) ÷ ab
(iii) (25x⁵ – 15x⁴) ÷ 5x³
(iv) (4l⁵ – 6l⁴ + 8l³) ÷ 2l²
(v) 15 (a³b²c² – a²b³c² + a²b²c³ ) ÷ 3abc
(vi) 3p³– 9p²q – 6pq²) ÷ (-3p)
(vii) (\(\frac{2}{3}\) a² b² c²+ \(\frac{4}{3}\) a b² c³) ÷ \(\frac{1}{2}\)abc
Solution:
(i) (3x² – 2x) ÷ x

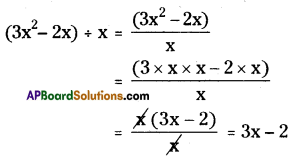
(ii) (5a³b – 7ab³) ÷ ab

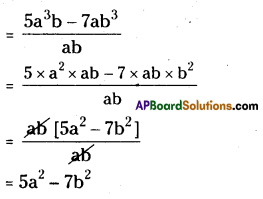
(iii) (25x⁵ – 15x⁴) ÷ 5x³

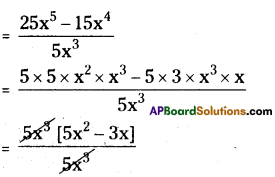
= 5x² – 3x (or) x(5x – 3)

(iv) (4l⁵ – 6l⁴ + 8l³) ÷ 2l²

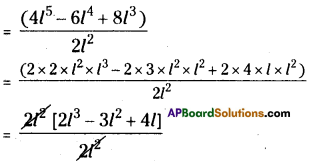
= 2l² – 3l² + 4l = l(2l² – 3l + 4)

(v) 15 (a³ b² c² – a² b³ c² + a² b² c³ ) ÷ 3abc

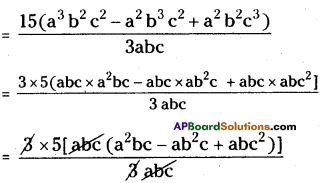
= 5[a x abc – b x abc + c x abc ]
= 5abc [a – b + c]

(vi) 3p³– 9p²q – 6pq²) ÷ (-3p)

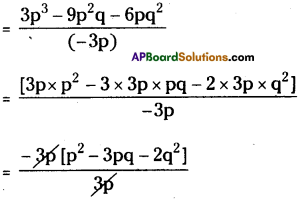
= -[p² – 3pq – 2q²]
= 2² + 3pq – p²

(vii) (\(\frac{2}{3}\) a²b²c²+ \(\frac{4}{3}\) ab²c³) ÷ \(\frac{1}{2}\)abc

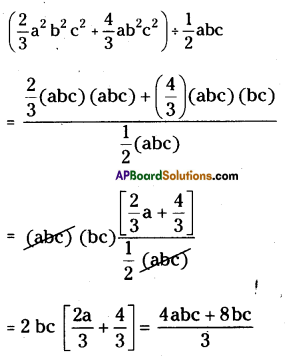
Question 3.
Workout the following divisions:
(i) (49x -63) ÷ 7
(ii) 12x (8x – 20,) ÷ 4(2x – 5)
(iii) 11a³ b³ (7c – 35) ÷ 3a² b² (c – 5)
(iv) 54lmn (l + m) (m + n) (n + l) ÷ 8 lmn (l + m) (n +l)
(v) 36(x + 4)(x² + 7x + 10) ÷ 9(x + 4)
(vi) a(a+1)(a+2)(a + 3) ÷ a(a + 3)
Solution:
(i) (49x -63) ÷ 7

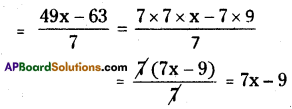
(ii) 12x (8x – 20,) ÷ 4(2x – 5)

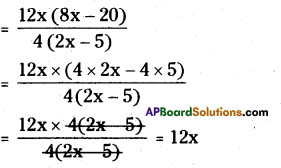
(iii) 11a³ b³ (7c – 35) ÷ 3a² b² (c – 5)

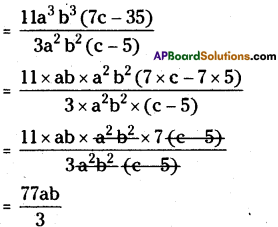
(iv) 54lmn (l + m) (m + n) (n + l) ÷ 8 lmn (l + m) (n +l)

(v) 36(x + 4)(x² + 7x + 10) ÷ 9(x + 4)

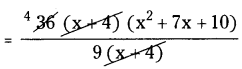
4 ( x² + 7x + 10)
= 4 ( x² + 5x + 2x + 10)
= 4 [x( x + 5) +2(x + 5)]
= 4( x + 5) (x + 2)

(vi) a(a+1)(a+2)(a + 3) ÷ a(a + 3)

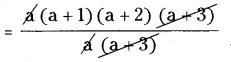
= ( a + 1)(a + 2)

Question 4.
Factorize the expressions and divide them as directed:
(i) (x² + 7x + 12) ÷ (x + 3)
(ii) (x² – 8x + 12) ÷ (x – 6)
(iii) (p² + 5p + 4,) (p + l)
(iv) 15ab(a² – 7a + 10) ÷ 3b(a – 2)
(v) 151m (2p² – 2q²) ÷ 3l(p + q)
(vi) 26z³(32z² – 18,) ÷ 13z² (4z – 3)
Solution:
(i) (x² + 7x + 12) ÷ (x + 3)
(x² + 7x + 12) ÷ (x + 3)
x² + 7x + 12 = x² + 3x + 4x + 12
= x(x + 3) + 4(x + 3)
= (x + 3) (x + 4)

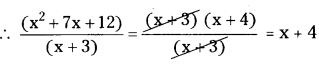
(ii) (x² – 8x + 12) ÷ (x – 6)
(x² – 8x + 12) ÷ (x – 6)
x² – 8x + 12 = x² – 6x – 2x + 12
= x(x – 6) – 2(x – 6)
= (x – 6) (x – 2)
∴ (x² – 8x + 12) 4 (x – 6)
= \(\frac{(x-6)(x-2)}{(x-6)}\) = x – 2

(iii) (p² + 5p + 4,) (p + 1)
p² + 5p + 4 = p² + p + 4p + 4
= p(p + 1) + 4(p + 1)
= (p + 1) (p + 4)
(p² + 5p + 4) ÷ (p + 1)
= \(\frac{(p+1)(p+4)}{(p+1)}\) = p + 4

(iv) 15ab(a² – 7a + 10) ÷ 3b(a – 2)
15ab (a² – 7a + 10) ÷ 3b (a – 2)
15ab (a² – 7a + 10) = 15ab (a² – 5a – 2a + 10)
= 15ab [(a² – 2a) – (5a -10)]
= 15ab [a(a – 2) – 5(a – 2)]
= 15ab(a – 2)(a – 5)
∴ 15ab (a² – 7a + 10) ÷ 3b (a – 2)

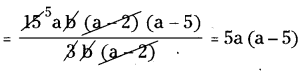
(v) 151m (2p² – 2q²) ÷ 3l(p + q)
15lm (2p² – 2q²) ÷ 3l (p + q)
15lm (2p² – 2q²) = 15lm x 2(p² – q²)
= 30lm (p + q) (p – q)
∴ 15lm(2p² – 2q²) ÷ 3l(p + q)

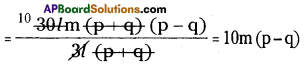
(vi) 26z³(32z² – 18,) ÷ 13z² (4z – 3)
26z³(32z² – 18) ÷ 13z² (4z – 3)
26z³(32z² – 18) = 26z³ (2 x 16z² – 2 x 9)
= 26z³ x 2 [16z³ – 9]
= 52z³ [(4z)³ – (3)³]
= 52z³ (4z + 3) (4z – 3)
∴ 26z³ (32z² – 18) ÷ 13z² (4z – 3)