AP State Syllabus 8th Class Maths Solutions 10th Lesson Direct and Inverse Proportions InText Questions
AP State Syllabus AP Board 8th Class Maths Solutions Chapter 10 Direct and Inverse Proportions InText Questions and Answers.
8th Class Maths 10th Lesson Direct and Inverse Proportions InText Questions and Answers
Do this
Question 1.
Write five more such situations where change in one quantity leads to change in another quantity. [Page No. 231]
Answer:
The change in one quantity leads to change in another quantity will see in the following situations.
- If speed increases then time decreases.
- In a family, the number of persons are increased then their consumption will also increases.
- If water consumption increases then water levels decreases.
- If the capacity of worker’s increases then time decreases.
- If thickness of a wire increases then its resistance decreases.
![]()
Question 2.
Write three situations where you see direct proportion. [Page No. 233]
Answer:
- The relation between number of students to number of teachers.
- Number of buffaloes to their consumption of grass.
- Number of workers to length of wall.
Question 3.
Let us consider different squares of sides 2, 3, 4 and 5 cm. Find the areas of the squares and fill the table.
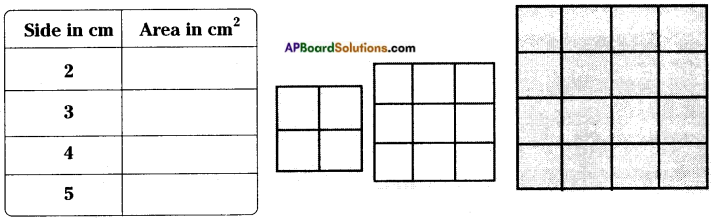
What do you observe? Do you find any change in the area of the square with a change in its side? Further, find the ratio between the area of a square to the length of its side. Is the ratio same? Obviously not.
∴ This variation is not a direct proportion. [Page No. 233]
Answer:

From the above table the ratios are not equal.
∴ So the change is not in direct proportion.
If the measure of side of a square will be change then its area also be changed.
![]()
Question 4.
The following are rectangles of equal breadth on a graph paper. Find the area for each rectangle and fill in the table.
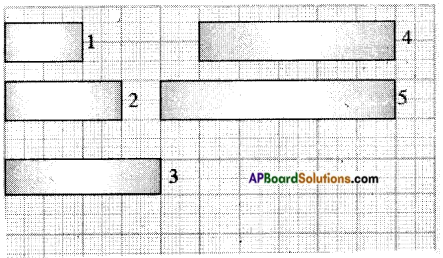

Is the area directly proportional to length? [Page No. 233]

Answer:
Yes, the area is directly proportional to its length.
![]()
Question 5.
Take a graph paper make same rectangles of same length and different width. Find the area for each. What can you conclude about the breadth and area? [Page No. 233]
Answer:

Area of first rectangle (A1) = 3 × 1 = 3 sq. cm.
Area of second rectangle (A2) = 3 × 2 = 6 sq. cm.
∴ The relation between the areas of rectangle and breadths is in direct proportion.
[∵ \(\frac{1}{3}\) = \(\frac{2}{6}\)]
Question 6.
Measure the distance in the given map and using that calculate actual distance between (i) Vijayawada and Visakhapatnam, (ii) Tirupati and Warangal. (Scale is given) [Page No. 235]
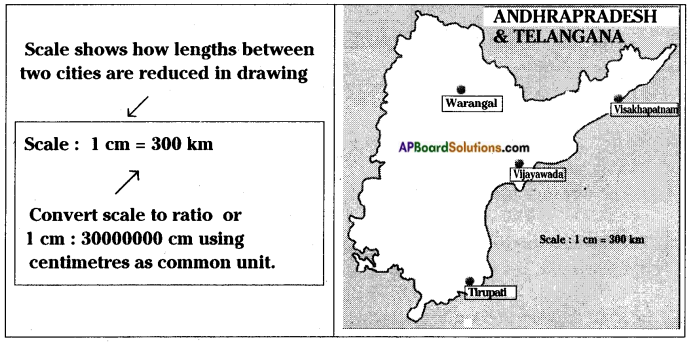
Answer:
i) The distance between Vijayawada and Visakhapatnam = 2 cm
According to the sum
1 cm = 300 km then 2 cm = ?
1 …… 300
2 …… ? (x)
⇒ x = 2 × 300 = 600 km
The distance between the above two cities is 600 km.
ii) The distance between Tirupathi and Warangal = 3 cm
But given that 1 cm = 300 km
3 cm = ? (x)
x = 3 × 300 = 900 km
∴ The distance between Tirupathi and Warangal = 900 km.
![]()
Question 7.
Write three situations where you see inverse proportion. [Page No. 238]
Answer:
i) Time – work capacity
ii) Speed – distance
iii) Time – speed
Question 8.
To make rectangles of different dimensions on a squared paper using 12 adjacent squares. Calculate length and breadth of each of the rectangles so formed. Note down the values in the following table.

What do you observe? As length increases, breadth decreases and vice-versa (for constant area).
Are length and breadth inversely proportional to each other? [Page No. 238]
Answer:
In a rectangle if length is increases then breadth is decreases and vise-versa.
∴ Length and breadth of a rectangle are in inverse proportion.
Think, discuss and write
![]()
Question 1.
Can we say that every variation is a proportion.
A book consists of 100 pages. How do the number of pages read and the number of pages left over in the book vary?

What happened to the number of left over pages, when completed pages are gradually increasing? Are they vary inversely? Explain. [Page No. 239]
Answer:
In every situation number of pages read and number of pages left over in the book are in inverse proportion.
If number of pages read are increases then number of pages left are decreases.

