AP Board 7th Class Maths Solutions Chapter 9 బీజీయ సమాసాలు InText Questions

SCERT AP 7th Class Maths Solutions Pdf Chapter 9 బీజీయ సమాసాలు InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson బీజీయ సమాసాలు InText Questions

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 98]

ప్రశ్న 1.
దిగువ పేర్కొన్న ప్రతి సమాసములలో ఎన్ని పదాలున్నాయో తెలపండి.
(i) 5x² + 3y + 7
సాధన.
పదాల సంఖ్య = 3

(ii) 5x²y + 3
సాధన.
పదాల సంఖ్య = 2

(iii) 3x²y
సాధన.
పదాల సంఖ్య = 1

(iv) 5x – 7
సాధన.
పదాల సంఖ్య = 2

(v) 7x³ – 2x
సాధన.
పదాల సంఖ్య = 2

ప్రశ్న 2.
పై సమాసాలలో సంఖ్యాపదాలను మరియు బీజీయ పదాలను గుర్తించి విడిగా రాయండి.
(i) 5x² + 3y + 7
సాధన.
సంఖ్యా పదాలు = 7
బీజీయ పదాలు = 5x² + 3y

(ii) 5x²y + 3
సాధన.
సంఖ్యా పదాలు = 3
బీజీయ పదాలు = 5x²y

(iii) 3x²y
సాధన.
సంఖ్యా పదాలు = లేవు
బీజీయ పదాలు = 3x²y

(iv) 5x – 7
సాధన.
సంఖ్యా పదాలు = -7
బీజీయ పదాలు = 5x

(v) 7x³ – 2x
సాధన.
సంఖ్యా పదాలు = లేవు
బీజీయ పదాలు = 7x³ – 2x

ప్రశ్న 3.
దిగువ ఇవ్వబడిన సమాసాలలోని పదాలను రాయండి. – 3x + 4, 2x – 3y, \(\frac{4}{3}\)a² + \(\frac{5}{2}\)b, 1.2ab + 5.1b – 3.2a
సాధన.
– 3x+4 లోని పదాలు = – 3x, 4
2x – 3y లోని పదాలు = 2x, – 3y
\(\frac{4}{3}\)a² + \(\frac{5}{2}\)b లోని పదాలు = \(\frac{4}{3}\)a², \(\frac{5}{2}\)b
1.2ab + 5.1b – 3.28 లోని పదాలు
= 1.2 ab, 5.1 b, – 3.2a

అన్వేషిద్దాం [పేజీ నెం. 100]

ప్రశ్న 1.
కింద ఇచ్చిన సమాసాలలో m² కలిగి ఉన్న పదాలను గుర్తించండి మరియు m యొక్క గుణకాలను రాయండి.

(i) mn² + m²n
సాధన.
m² ను కలిగిన పదం = m²n
m² గుణకము = n

(ii) 7m² – 5m – 3
సాధన.
m² ను కలిగిన పదం = 7m²
m² గుణకము = 7

(iii) 11 – 5m² + n + 8 mm
సాధన.
m² ను కలిగిన పదం = – 5m²
m² యొక్క గుణకము = – 5

నీ ప్రగతిని సరిచూసుకో [పేజీ నెం. 104]

ప్రశ్న 1.
దిగువ పేర్కొన్న పదాలలో సజాతి పదాలను రాయండి:
– xy², – 4yx, 8x, 2xy², 7y, – 11x², – 100x, – 11yx, 20x²y, – 6x², y, 2xy, 3x
సాధన.
సజాతి పదాలు:
(i) – xy², 2xy²
(ii) – 4yx, – 11yx, 2xy
(iii) 8x, – 100x, 3x
(iv) 7y, y
(v) – 11x², – 6x²

ప్రశ్న 2.
(i) 3x²y, (ii) – ab²c అను పదాలకు మూడు సజాతి పదాలను రాయండి.
(i) 3x²y
సాధన.
3x²y కి మూడు సజాతి పదాలు
= 2x²y, – x²y, 4 x²y

(ii) – ab²c
సాధన.
– ab²c కి మూడు సజాతి పదాలు
= 2ab²c, 3ab²c, – 4 ab²c

అన్వేషిద్దాం [పేజి నెం. 104]

ప్రశ్న 1.
జాస్మిన్ 3xyz అనునది త్రిపది అని చెప్పింది. ఆమె చెప్పింది సరైనదా? కారణం ఇవ్వండి.
సాధన.
ఇవ్వబడిన సమాసం 3xyz.
ఈ సమాసములో ఒకే ఒక పదం ఉన్నది. కావున, ఇది ఏకపది. త్రిపది కాదు.
కావున, జాస్మిన్ చెప్పినది సరైనది కాదు.

ప్రశ్న 2.
ఏకపది, ద్విపదులకు ఏవేని రెండేసి ఉదాహరణలు ఇవ్వండి.
సాధన.

సమాసాల రకం	సమాసాలు
ఏకపది	X, b2c, xy2z, ……
ద్విపది	x + 2y, 4b – 3c, x2y – yz, ……..

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 108]

ప్రశ్న 1.
కింది సజాతి పదాల మొత్తాన్ని కనుగొనండి.
(i) 12ab, 9ab, ab
సాధన.
12ab, 9ab, ab ల మొత్తం
= 12ab + 9ab + ab
= (12 + 9 + 1) ab
= 22 ab

(ii) 10x², – 3x², 5x²
సాధన.
= 10x² + (- 3x²) + 5x² ల మొత్తం
= [10x² + (-3) + 5) x² = 12x²

(iii) – y², 5y², 8y, – 14y²
సాధన.
– y², 5y², 8y², – 14y² ల మొత్తం
= (- y²) + 5y² + 8y² + (- 14y²)
= [(- 1) + 5 + 8 + (- 14)] y²
= [13 + (- 15)] y²
= – 2y²

(iv) 10mn, 6mn, – 2mn, – 7mn
సాధన.
10mm, 6mn, – 2mn, – 7mm ల మొత్తం
= 10mn + 6mm + (- 2mm) + (- 7mm)
= [10 + 6 + (- 2) + (- 7]] mn
= [16 + (- 9]] mn = 7 mn

ఆలోచించండి [పేజి నెం. 108]

రేష్మా 4p + 6p + p అను సమాసాన్ని కింది విధముగా సూక్ష్మీకరించింది. 4p + 6p + p = 10p ఆమె చేసింది సరైనదేనా ? సమర్ధించుము.
సాధన.
రేష్మా 4p + 6p + p= 10p గా సూక్ష్మీకరించడము సరైనది కాదు.
ఎందుకనగా 4p + 6p + p = 11p

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 110]

ప్రశ్న 1.
క్రింది సమాసాల యొక్క ప్రామాణిక రూపాన్ని రాయండి:
(i) – 51 + 2l² + 4
సాధన.
– 5l + 2l² + 4 యొక్క ప్రామాణిక రూపం
= 2l² – 5l + 4

(ii) 4b² + 5 – 3b
సాధన.
4b² + 5 – 3b యొక్క ప్రామాణిక రూపం
= 4b² – 3b + 5

(iii) z – y – x
సాధన.
z – y – x యొక్క ప్రామాణిక రూపం
= z – y – x లేదా – x – y + z

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 112]

ప్రశ్న 1.
కింద ఇచ్చిన సమాసాలను అడ్డు వరుస మరియు నిలువు వరుసల పద్ధతిలో కూడండి.
(i) x – 2y, 3x + 4y
సాధన.
అడ్డు వరుస పద్ధతి:
= (x – 2y) + (3x + 4y)
= x + 3x – 2y + 4y
= (1 + 3)x + (- 2 + 4)y
= 4x + 2y

నిలువు వరుస పద్ధతి:

(ii) 4m² – 7n² + 5mn, 3n² + 5m² – 2mn.
సాధన.
అడ్డు వరుస పద్ధతి:
(4m² – 7n² + 5mn) + (3n² + 5m² – 2mm)
= 4m² + 5m² – 7n² + 3n² + 5mn – 2mn
= (4 + 5)m² + (- 7 + 3)n² + (5 – 2)mn
= 9m² – 4n² + 3mm

నిలువు వరుస పద్ధతి:

(గమనిక : సజాతి పదాల కింద సజాతి పదాలు రాయాలి.)

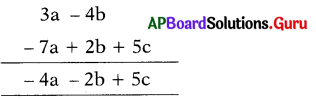
(iii) 3a – 4b, 5c – 7a + 2b
సాధన.
అడ్డు వరుస పద్ధతి:
(3a – 4b) + (5c – 7a + 2b)
= 3a – 7a – 4b + 2b + 5c
= – 4a – 2b + 5c

నిలువు వరుస పద్ధతి:

అన్వేషిద్దాం [పేజి నెం. 112]

ఏవేని కనీసం రెండు సందర్భాలకు బీజీయ సమాసాలను ఏర్పరచి, వాటిని సంకలనము చేయండి.
సాధన.
x కు 3 రెట్లు కన్నా నాలుగు తక్కువ = 3x – 4
x కు రెట్టింపుకు 5 ఎక్కువ = 2x + 5
3x – 4 మరియు 2x + 5 ల సంకలనము

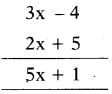
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 114]

ప్రశ్న 1.
కింద ఇచ్చిన పదాలలో రెండవ పదం నుంచి మొదటి – పదాన్ని తీసివేయండి.
(i) 2xy, 7xy
సాధన.
7xy – 2xy = 7xy + (- 2xy) = 5xy
(2xy కి సంకలన విలోమం – 2xy)

(ii) 4a², 10a²
సాధన.
10a² – 4a² = 10a² + (- 4a²) = 6a²

(iii) 15p, 3p
సాధన.
3p – 15p = 3p + (- 15p) = – 12p

(iv) 6m²n, – 20m²n
సాధన.
– 20 m²n – 6m²n = – 20m²n + (- 6m²n)
= – 26m²n

(v) a²b², – a²b²
సాధన.
(- a²b²) – a²b² = – a²b² + (- a²b²)
= – 2a²b2²

అన్వేషిద్దాం [పేజి నెం. 116]

అడ్డువరుస మరియు నిలువు వరుసల పద్ధతిలో కింద పేర్కొన్న బీజీయ సమాసాల కూడిక మరియు తీసివేతలను కనుగొనండి: x – 4y + z, 6z – 2x + 2y.
సాధన.
కూడిక అడ్డు వరుస పద్ధతి :
(x – 4y + z) + (6z – 2x + 2y)
= x – 4y + z + 6z – 2x + 2y
= x + (- 2x) + (- 4y) + 2y + z + 6z
= [1 + (- 2)]x + [(- 4) + 2]y + (1 + 6)z
= – 1x + (- 2)y + 7z
= – x – 2y + 7z

నిలువు వరుస పద్ధతి

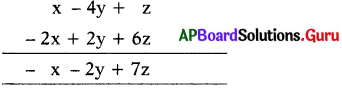
తీసివేత
అడ్డు వరుస పద్ధతి:
x – 4y + z, – 2x + 2y + 6z
A = x – 4y + z, B = – 2x + 2y + 6z అనుకొనుము.
B యొక్క సంకలన విలోమం – B.
– B = – (- 2x + 2y + 6z)
– B = 2x – 2y – 6z
A + B = A + (- B)
= (x – 4y + z) + (2x – 2y – 6z)
= x – 4y + z + 2x – 2y – 62
= (1 + 2)x + (- 4 – 2)y + (1 – 6)z
∴ A – B = 3x – 6y – 5z

నిలువు వరుస పద్దతి:
x – 4y + z, – 2x + 2y + 6z
A = x – 4y + z,
B = – 2x + 2y + 6z అనుకొనుము.

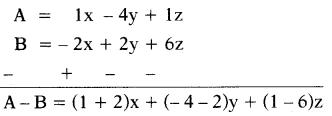
= 3x + (- 6)y + (- 5)z
∴ A – B = 3x – 6y – 5z

అన్వేషిద్దాం [పేజి నెం. 120]

ప్రశ్న 1.
x = – 5 అయినపుడు సమాసము విలువ -15 అయ్యేటట్లు ఒక బీజీయ సమాసాన్ని రాయండి.
సాధన.
x = – 5 మరియు విలువ = – 15 అని ఇవ్వబడినది.
విలువ = – 15
= 3 × – 5
= 3 × x (∵ x = – 5)
∴ సమాసం = 3x

ప్రశ్న 2.
x = 2 అయినపుడు సమాసము విలువ 15 అయ్యేటట్లు ఒక బీజీయ సమాసాన్ని రాయండి.
సాధన.
x = 2 మరియు విలువ = 15 అని ఇవ్వబడినది. విలువ = 15
= \(\frac{30}{2}\) = \(\frac{1}{2}\) × 15 × 2
= \(\frac{1}{2}\) × 15 × 2 (∵ x = 2)
∴ సమాసం = \(\frac{15 x}{2}\)

[అలోచించండి పేజి నెం. 120]

x = – 2 అయినప్పుడు 5x అనే బీజీయ సమాసము యొక్క విలువను కనుగొనేటప్పుడు ఇద్దరు విద్యార్థులు దిగువ పేర్కొన్న విధంగా సమాధానం ఇచ్చారు.

ఎవరు సరిగ్గా చేసారో ఊహించగలరా ? మీ సమాధానాన్ని సమర్థించండి !
సాధన.
చైతన్య సరిగ్గా చేశాడు.
5x అనగా 5 × x అని అర్థం.
x = – 2 అయినపుడు 5x = 5 × (- 2) అవుతుంది.
5 × (- 2) = – 10
రీటా 5x అనగా 5 నుండి 2 ను తీసివేసినది. కావున రీటా చేయడం తప్పు.

తార్కిక విభాగం కోడింగ్ మరియు డీకోడింగ్ [పేజి నెం. 126]

సమాచారాన్ని గుర్తులు, సంకేతాలు రూపంలో మార్చడాన్ని కోడింగ్ అంటారు. ఆ సంకేతాలను అనుసరించి తిరిగి సమాచార రూపంలోకి మార్చడాన్ని డీకోడింగ్ అంటారు. కోడింగ్ మరియు డీకోడింగ్ కు చాలా పద్ధతులున్నాయి. మనం దానిని విభిన్న మార్గాల్లో సరిచూడవచ్చును.

గుర్తుల లాజిక్, విభిన్న అమరికల్లో ఆంగ్ల అక్షరాలను మార్చడం, అక్షరాల యొక్క స్థానాల క్రమము, అక్షరాల యొక్క స్థానాలకు కేటాయించిన సంఖ్యా విలువలు వంటి కొన్ని విధానాలను మనం చర్చిద్దాం. ఈ ముందు మరియు వ్యతిరేక దిశల్లో అక్షర క్రమంలో అక్షరాలకు సంఖ్యలను కేటాయించడం ద్వారా మనం ఒక పట్టికని తయారు చేయాలి. ఇది కొన్ని సమస్యలను డీకోడింగ్ చేయడానికి సహాయపడుతుంది.

ఆంగ్ల అక్షర సంఖ్యాపట్టిక:

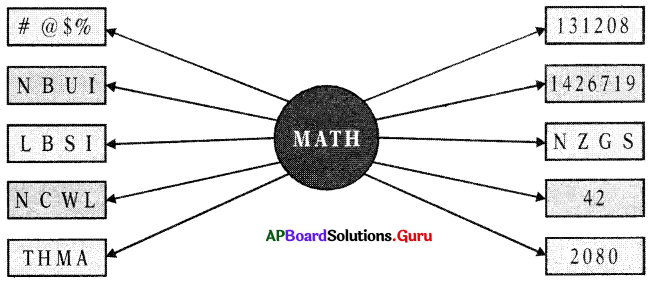
కోడింగ్ మరియు డీకోడింగ్ కు సంబంధించిన కొన్ని ఉదాహరణలను దిగువ టేబుల్ నుంచి మనం నేర్చుకుందాము.

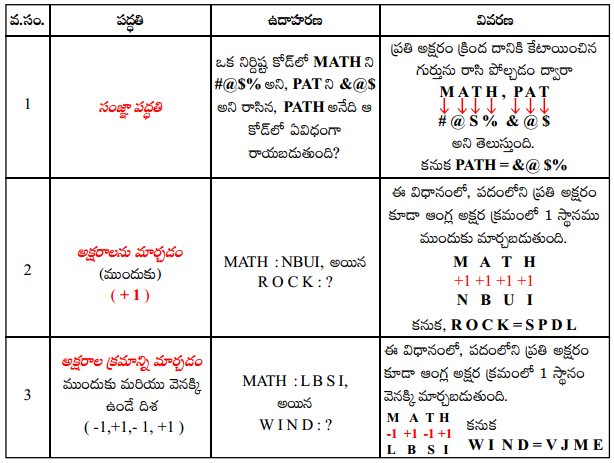
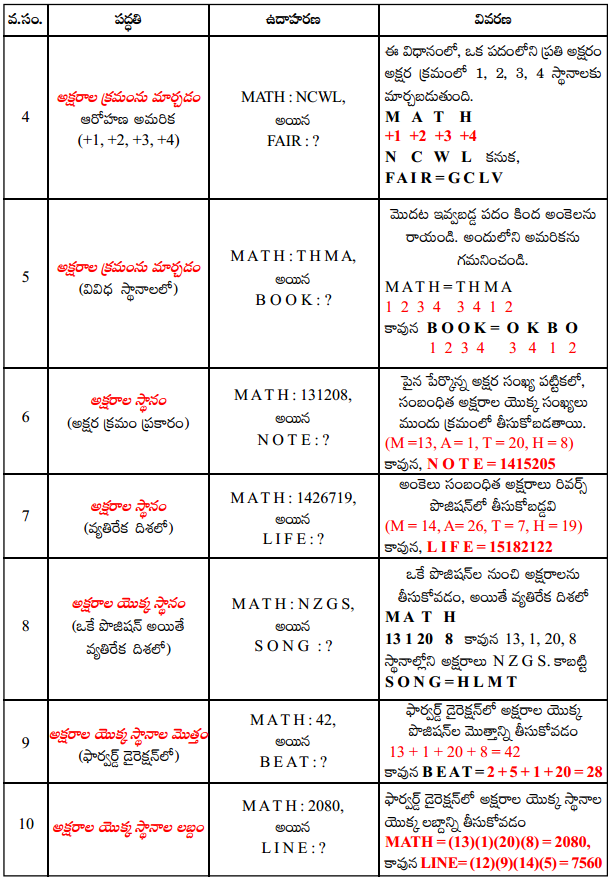
ఉదాహరణలు

ప్రశ్న 1.
దిగువ పేర్కొన్న ప్రతి సమాసాలలో ఎన్ని పదాలున్నాయో తెలపండి.
(i) a + b
సాధన.
a + b లో పదాల సంఖ్య = 2

(ii) 3t²
సాధన.
3t² లో పదాల సంఖ్య = 1

(iii) 9p³ + 10q – 15
సాధన.
9p³ + 10q – 15 లో పదాల సంఖ్య = 3

(iv) \(\frac{5 m}{3 n}\)
సాధన.
\(\frac{5 m}{3 n}\) లో పదాల సంఖ్య = 1

(v) 4x + 5y – 3z – 1
సాధన.
4x + 5y – 3z – 1 లో పదాల సంఖ్య = 4

ప్రశ్న 2.
దిగువ ఇవ్వబడ సమాసాలలో పదాల సంఖ్యను రాయండి. సంఖ్యాసమాసము మరియు బీజీయ సమాసములను గుర్తించండి.
(i) 8p
సాధన.
8p – 1 పదము – బీజీయ సమాసము

(ii) – 3 – 11
సాధన.
-3 – 11 – 2 పదములు – సంఖ్యా సమాసము

(iii) 5c + s – 7
సాధన.
5c + s – 7 – 3 పదములు – బీజీయ సమాసము

(iv) – 6
సాధన.
– 6 – 1 పదము – సంఖ్యా సమాసము

(v) (2 + 1) – 6
సాధన.
(2 + 1) – 6 – 2 పదములు – సంఖ్యా సమాసము

(vi) 9t + 15
సాధన.
9t + 15 – 2 పదములు – బీజీయ సమాసము

ప్రశ్న 3.
ఇచ్చిన పదాలకు గుణకాలను రాయండి.
(i) 8pq లో p గుణకము
సాధన.
8pq = p(8q) కావున, p యొక్క గుణకము 8q అగును.

(ii) \(\frac{x y}{3}\) లో x గుణకము
సాధన.
\(\frac{x y}{3}\) = x\(\left(\frac{y}{3}\right)\) కావున,
\(\frac{x y}{3}\) లో x యొక్క గుణకము \(\left(\frac{y}{3}\right)\) అగును.

(iii) (- abc) లో abc గుణకము
సాధన.
(- abc) = – (abc) కావున, abc యొక్క గుణకము – 1 అగును.

ప్రశ్న 4.
దిగువ పేర్కొన్న పదాలలో సజాతి పదాలను గుర్తించి, సమూహాలుగా రాయండి.
10ab, 7a, 8b, – a²b², – 7ba, – 105b, 9b²a², – 5a², 90a.
సాధన.
(7a, 90a) ఒకే బీజీయ కారణాంకాలను ‘a’ కలిగి ఉండడం వలన ఇవి సజాతి పదాలు అవుతాయి.
(10ab, – 7ba) ఒకే బీజీయ కారణాంకాలను ‘ab’ కలిగి ఉండడం వల్ల ఇవి సజాతి పదాలు అవుతాయి.
(8b, – 105b) ఒకే బీజీయ కారణాంకాలను ‘b’ కలిగి ఉండడం వల్ల ఇవి సజాతి పదాలు అవుతాయి.
(- a²b², 9b²a²) ఒకే బీజీయ కారణాంకాలను ‘a²b²‘ కలిగి ఉండడం వల్ల ఇవి సజాతి పదాలు అవుతాయి.

ప్రశ్న 5.
దిగువ బీజీయ సమాసాలను ఏకపద, ద్విపద, త్రిపదులుగా వర్గీకరించండి. కారణాలను పేర్కొనండి.
a + 4b, 3x²y, px² + qx + 2, qz², x² + 2y, 7xyz, 7x² + 9y³ – 10z⁴, 3l² – m², x, – abc
సాధన.

బీజీయ సమాసము	బీజీయ సమాసాల రకం	కారణము
x, 7xyz 3x2y, qz2, – abc	ఏకపది	ఒక పదం
a + 4b, x2 + 2y, 3l2 – m2	ద్విపది	రెండు విజాతి పదాలు
px2 + qx + 2, 7x2 + 9y3 – 10z4	త్రిపది	మూడు విజాతి పదాలు

ప్రశ్న 6.
కింది సజాతి పదాల మొత్తాన్ని కనుక్కోండి.
(i) 3a, 9a
సాధన.
3a, 9a ల మొత్తము = 3a + 9a
= (3 + 9)a = 12a

(ii) 5p²q, 2p²q.
సాధన.
5p²q, 2p²q ల మొత్తము
= 5p²q + 2p²q
= (5 + 2) p²q = 7p²q

(iii) 6m, – 15m, 2m
సాధన.
6m, – 15m, 2m ల మొత్తము
= 6m + (- 15m) + 2m
= 6m – 15m + 2m
= (6 – 15 + 2)m = – 7m

ప్రశ్న 7.
క్రింద ఇవ్వబడిన పటము యొక్క చుట్టుకొలత కనుగొనుము.

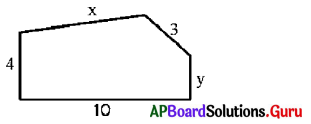
సాధన.
పటము యొక్క చుట్టుకొలత
P = 10 + 4 + x + 3 + y
= x + y + (10 + 4 + 3)
= x + y + 17

ప్రశ్న 8.
6a² + 3ab + 5b² – 2ab – b² + 2a² + 4ab + 2b² – a² సూక్ష్మీకరించండి.
సాధన.
6a² + 3ab + 5b² – 2ab – b² + 2a² + 4ab + 2b² – a²
= (6a² + 2a² – a²) + (3ab – 2ab + 4ab) + (5b² – b² + 2b²)
= [[6 + 2 – 1) a²] + [(3 – 2 + 4)ab] + [(5 – 1 + 2)b²]
= 7a² + 5ab + 6b²

ప్రశ్న 9.
2x² – 3x + 5 మరియు 9 + 6x² లను నిలువు వరుస పద్ధతిలో కూడండి.
సాధన.

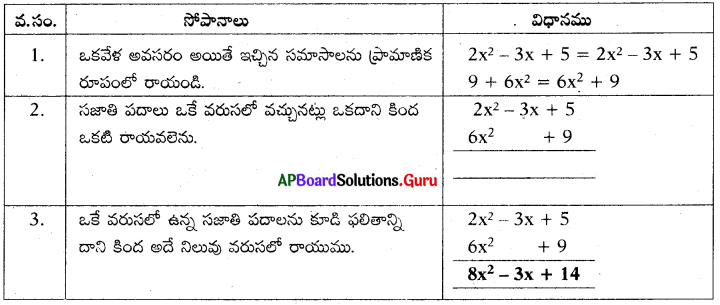
ప్రశ్న 10.
దిగువ సమాసాల యొక్క సంకలన విలోమాన్ని కనుగొనండి.
(i) 35
(ii) – 5a
(iii) 3p – 7.
(iv) 6x² – 4x + 5.
సాధన.
35 యొక్క సంకలన విలోమం = – 35
– 5a యొక్క సంకలన విలోమం = – (- 5a) = 5a
3p – 7 యొక్క సంకలన విలోమం = – (3p – 7) = – 3p + 7
6x² – 4x + 5 యొక్క సంకలన విలోమం
= – (6x² – 4x + 5)
= – 6x² + 4x – 5

ప్రశ్న 11.
9p² – 8 నుండి 2p² – 3 ను తీసివేయుము.
సాధన.
9p² – 8 – (2p² – 3) = 9p² – 8 – 2p² + 3
= (9 – 2) p² – 8 + 3
= 7p² – 5

ప్రశ్న 12.
6a – 2b + 3c నుంచి 3a + 4b – 2c ని అడ్డువరుస పద్ధతిలో తీసివేయుము.
సాధన.
A = 6a – 2b + 3c, B = 3a + 4b – 2c అనుకొనుము.
6a – 2b + 3c నుంచి 3a + 4b – 2c ని తీసివేయడము అనేది 6a – 2b + 3C కి
3a + 4b – 2c యొక్క సంకలన విలోమాన్ని కూడుటకు సమానము. అనగా
A – B = A + (- B)
(3a + 4b – 2c) యొక్క సంకలన విలోమం
= – (3a + 4b – 2c) = – 3a – 4b + 2c
A – B = A + (- B)
= 6a – 2b + 3c + (-3a – 4b + 2c)
= 6a – 2b + 3c – 3a – 4b + 2c
= (6 – 3)a – (2 + 4)b + (3 + 2)c
అయిన, కావలసిన ఫలితము = 3a – 6b + 5c

ప్రశ్న 13.
6m³ + 4m² + 7m – 3 నుంచి 3m³ + 4 ని దశలవారీ పద్ధతి (సోపాన పద్ధతి)లో తీసివేయుము.
సాధన.
ఈ సమస్యని దశల వారీగా సాధిద్దాం.
సోపానము 1:
6m³ + 4m² + 7m – 3 – (3m² + 4)
సోపానము 2:
6m³ + 4m² + 7m – 3 – 3m² – 4
సోపానము 3:
6m³ – 3m³ + 4m² + 7m – 3 – 4
(సజాతీయ పదాలను ఒకచోట వ్రాయగా)
సోపానము 4: (6 – 3)m³ + 4m² + 7m – 7 (విభాగ న్యాయము)
కావలసిన ఫలితము = 3m³ + 4m² + 7m – 7

ప్రశ్న 14.
3n² + 5m² – 2mm నుంచి 4m² – 7n² + 5mm ని తీసివేయుము.
(సులభంగా అర్థము చేసుకోవడానికి ఒకే రకమైన సజాతి పదాలకు ఒకే రంగులను ఇవ్వడం జరిగింది)
సాధన.

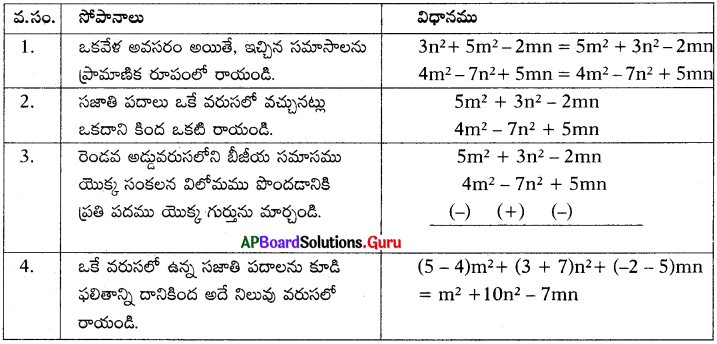
ప్రశ్న 15.
x = 3 వద్ద ఇచ్చిన సమాసాల విలువను కనుగొనుము.
(i) x + 6
సాధన.
x = 3 వద్ద x + 6 (xకి బదులుగా 3ని ప్రతిక్షేపించిన) = (3) + 6 = 9

(ii) 8x – 1
సాధన.
x = 3 వద్ద 8x – 1 యొక్క విలువ = 8(3) – 1 = 24 – 1 = 23

(iii) 14 – 5x
సాధన.
x = 3 వద్ద 14 – 5x యొక్క విలువ = 14 – 5(3) = 14 – 15 = – 1

సాధనా ప్రశ్నలు [పేజి నెం. 130]

ప్రశ్న 1.
ఒక నిర్దిష్ట కో లో BOARD: CNBQE, అయిన అదే కో లో ANGLE అనునది
(a) BMHKF
(b) CNIJE
(c) BLGIF.
(d) CMIKF
సాధన.
(a) BMHKF

వివరణ:

ప్రశ్న 2.
ఒక నిర్దిష్ట కో లో MOBILE : 56, అయిన PHONE అనునది
(a) 52
(b) 54
(c) 56
(d) 58
సాధన.
(d) 58

వివరణ:

ప్రశ్న 3.
BEAN: ABNE అయిన NEWS?
(a) WSNE
(b) WSEN
(c) WNSE
(d) WNES
సాధన.
(c) WNSE

వివరణ:

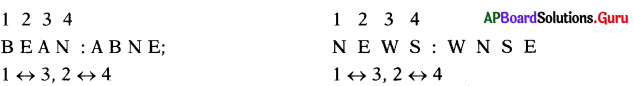
పదంలో 1వ అక్షరం 3వ అక్షరంగా, 3వ అక్షరం 1వ అక్షరంగా, అలాగే 2, 4 అక్షరాలు వాని స్థానాలను మార్చుకొన్నాయి.

ప్రశ్న 4.
ROSE : 6821, CHAIR : 73456, PREACH: 961473 అయిన SEARCH?
(a) 241673
(b) 214673
(c) 216473
(d) 216743
సాధన.
(b) 214673

వివరణ:
ROSE : 6821.
CHAIR : 73456
PREACH : 961473
SEARCH : ?
(పదంలోని అక్షరాల సంఖ్య కోడ్ చేయబడిన సంఖ్యలోని అంకెల సంఖ్య సమానం.. కావున ప్రతి అంకె ఒక అక్షరానికి కోడ్ చేయబడినది)
R → 6, (ROSEలో మొదటి అక్షరం, CHAIR లో చివరి అక్షరం, అలాగే PREACH లో 2వ అక్షరం).
0 → 8, S → 2, E → 1 (ROSEలో చివరి అక్షరం, PREACH లో 3వ అక్షరం).
P → 9, H → 3 (CHAIRలో 2వ అక్షరం, అలాగే PREACH లో చివరి అక్షరం).
A → 4, C → 7, I → 5
∴ SEARCH : 214673

ప్రశ్న 5.
COMPUTER: RFUVQNPC అయిన MEDICINE ?
(a) EDJOJMEF
(b) EOJDJEFM
(c) EOJJDFEM
(d) EDJJOFME
సాధన.
(b) EOJDJEFM

వివరణ:COMPUTER : RFUVQNPC
అక్షరాలను వ్యతిరేక దిశలో రాస్తూ మొదటి చివరి అక్షరాలను అలాగే రాయాలి మిగిలినవి + 1 క్రమంలో రాయాలి.

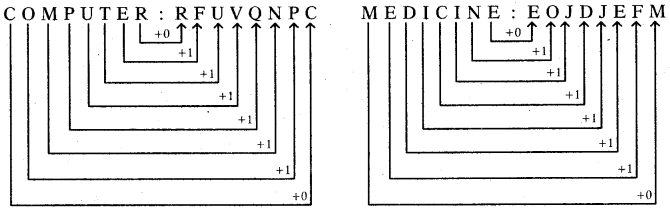
ప్రశ్న 6.
LAKE = 7@$5, WALK = %@7$ అయిన WAKE = ?
(a) @%75
(b) %@$5
(c) %5@7
(d) %@57
సాధన.
(b) %@$5

వివరణ:

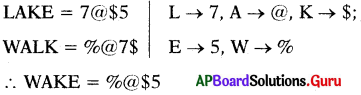
ప్రశ్న 7.
MANY = OCPA అయిన LOOK = ?
(a) NQQM
(b) MQQN
(c) QMQN
(d) QNQM
సాధన.
(a) NQQM

వివరణ:

ప్రశ్న 8.
SOME = PLJB అయిన BODY = ?
(a) LABY
(b) YBAL
(c) YLAV
(d) ABLY
సాధన.
(c) YLAV

వివరణ:

ప్రశ్న 9.
ARC = CVI అయిన RAY = ?
(a) TEU
(b) TEE
(c) TED
(d) TEF
సాధన.
(b) TEE

వివరణ:

ప్రశ్న 10.
MEAN = KGYP అయిన MODE = ?
(a) QBGK
(b) KBQG
(c) KGBQ
(d) KQBG
సాధన.
(d) KQBG

వివరణ:

ప్రశ్న 11.
FIND = DNIF అయిన DONE = ?
(a) ENOD
(b) ENDO
(c) NEOD
(d) ONED
సాధన.
(a) ENOD

వివరణ:
FIND = DNIF; DONE = ENOD
(అక్షరాలను వ్యతిరేక క్రమంలో రాయాలి).

ప్రశ్న 12.
BASE = SBEA అయిన AREA = ?
(a) AARE
(b) EAAR
(c) EARA
(d) REAA
సాధన.
(b) EAAR

వివరణ:

ప్రశ్న 13.
LESS = 55 అయిన MORE = ?
(a) 54
(b) 50
(c) 51
(d) 52
సాధన.
(c) 51

వివరణ:

(అక్షర సంఖ్యా పట్టికలో పై వరుస సంఖ్యలు తీసుకున్నాము).

ప్రశ్న 14.
BACK = 17 అయిన CELL = ?
(a) 33
(b) 30
(c) 31
(d) 32
సాధన.
(d) 32

వివరణ:

ప్రశ్న 15.
BIG = 63 అయిన SMALL = ?
(a) 76
(b) 78
(c) 74
(d) 72
సాధన.
(b) 78

వివరణ:

(అక్షర సంఖ్యా పట్టికలో క్రింది వరుస సంఖ్యలు ఉపయోగించాము).