SCERT AP 7th Class Maths Solutions Pdf Chapter 7 Ratio and Proportion Ex 7.4 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 7th Lesson Ratio and Proportion Ex 7.4
Question 1.
If 5 men take 8 days to type 10 books, then how many days does it take for 8 men to type 2 books?
Answer:
| Number of Men | Number of books typed | Number of Days |
| 5 | 10 | 8 |
| 8 | 2 | x |
Here the 3 quantities are men, books typed and number of days.
Let the number days taken to type 2 books by 8 men be x.
From the above,
- Number of days and men are in inverse proportion.
- Number of days and typed books are in direct proportion.
Here number of days depends on both men and number of books typed.
So, we have to take compound ratio of 8 : 5 and 10:2.
8 : x = 8 × 10 : 5 × 2
Since the ratios are equal,
The product of means = The product of extremes
⇒ 8 : x = 80 : 10
⇒ x × 80 = 8 × 10
⇒ \(\frac{80 x}{80}=\frac{80}{80}\)
⇒ x= 1 day
Or
x = \(\frac{5}{8} \times \frac{2}{10}\) × 8 = 1
∴ Number of days taken to type 2 books by 8 men is 1.
![]()
Question 2.
If 5 men take 9 days to plough 18 acres of land, then find how long it takes 25 men for to plough 30 acres?

Answer:
Here we have three quantities number of men, jj number of days and acres of land ploughed.
| Number of Men | Number of Land | Number of Days |
| 5 | 18 | 9 |
| 25 | 30 | X |
Let the number of days taken to plough the 30 acres of land by 25 men is x.
From the above,
- Number of days and number of men are in increase proportion.
- Number of days and acres of land ploughed in direct proportion.
Here number of days depends on both men and number of acres of land ploughed.
So, we have to take compound ratio of 25 : 5 and 18 : 30 is
25 × 18 : 5 × 30
∴ 9 : x = 25 × 18 : 5 × 30
Since the ratios are equal,
The product of means = The product of extremes
⇒ x × 25 × 18 = 9 × 5 × 30
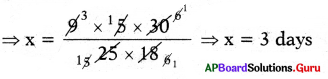
Or
x = \(\frac{5}{25} \times \frac{30}{18}\) × 9 = 3 days
∴ Number of days taken to plough 30 acres of land by 25 men is 3 days.
Question 3.
Rice cost ₹ 480 is needed for 8 members for 20 days. What is the cost of rice required for 12 members for 15 days?
Answer:
Here we have three quantities cost of rice, needed members and number of days.
| Number of Members | Number of Days | Cost of Rice |
| 8 | 20 | ₹ 480 |
| 12 | 15 | X |
Let the Cost of rice needed for 12 members for 15 days is x.
From the above,
• Number of members and number of days are in inverse proportion.
• Number of days and cost of rice are in direct proportion.
Here the cost of rice depends on both number of member needed and number of days.
So, we have to take compound ratio of 8 : 12 = 20 : 15 is
8 × 20: 12 × 15
480 : x = 8 × 20 : 12 × 15 Since the ratios are equal,
The product of means = The product of extremes
⇒ x × 8 × 20 = 480 × 12 × 15
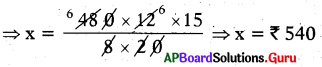
∴ The cost of rice needed for 12 members for 15 days is ₹ 540.
![]()
Question 4.
24 men working at 8 hours per day can dp a piece of work in 15 days. In how many days can 20 men working at 9 hours per day do the same work?
Answer:
Here we have three quantities number of men, working hours per day and number of days.
| Number of Men | Working hours | Number of Days |
| 24 | 8 | 15 |
| 20 | 9 | x |
Let the number of days needed for 20 men working at 9 hours is x.
From the above,
• Number of men and members are in inversely proportional:
• Number of men and their working hours per day are in direct proportion.
Here the number of days depends on both number of men and working hours per day.
So, we have to take compound ratio of 24 : 20 = 8 : 9 is
24 × 8 : 20 × 9
∴ x : 15 = 24 × 8 : 20 × 9
Since the ratios are equal,
The product of means = The product of extremes
⇒ x × 20 × 9 = 15 × 24 × 8
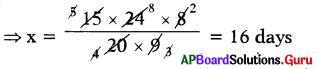
∴ The number of days needed fur 20 men working at 9 hours is 16 days.
Question 5.
12 painters can paint a wall of 180 meters long in 3 days. How many painters are required to paint 200 meters long wall in 5 days?
Answer:
Here we have three quantities number of painters, length of wall and number of days required.
| Length of wall | Number of working days | Number of Painters |
| 180 | 3 | 12 |
| 200 | 5 | X |
Let the number of painters needed to paint 200 m long wall in 5 days is x.
From the above,
- Number of working days and number of painters are in inversely proportional.
- Number of working days and length of wall are in direct proportion.
Here the number of painters depends on both number of working days and length of wall.
So, we have to take compound ratio of 180 :,200 = 5 : 3 is 180 × 5 : 200 × 3
∴ 12 : x = 180 × 5 : 200 × 3
Since the ratios are equal,
The product of means = The product of extremes
⇒ x × 180 × 5 = 12 × 200 × 3

⇒ x = 8
The number of painters needed to paint 200 m long wall in 5 days is 8.
