AP State Syllabus AP Board 7th Class Maths Solutions Chapter 6 Ratio – Applications Ex 6 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 6th Lesson Ratio – Applications Exercise 6
![]()
Question 1.
How long will it take for a sum of ₹ 12600 invested at 9% per annum beocme to ₹ 15624?
Solution:
HereA = ₹ 15,624 R = 9% T = ?
P = ₹ 12,600
∴ I = A – P = 15,624 – 12,600 = ₹ 3024
Also I = \(\frac{P R T}{100}\)
∴ 3024 = \(\frac{12,600 \times 9 \times \mathrm{T}}{100}\)
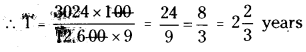
Question 2.
At what rate a sum doubles itself in 8 year 4 months?
Solution:
Given that A = double the sum
Let the principle be P
then A = 2P
T =8 years 4 months = 8y \(\frac { 4 }{ 12 }\) y = 8\(\frac { 1 }{ 3 }\) years = \(\frac { 25 }{ 3 }\)
R = R% say
We know that
I = \(\frac{\text { PTR }}{100}\)
Here I = A – P
= 2P – P = P
∴ P = \(\frac{P \cdot \frac{25}{3} \times R}{100}\)
∴ R = 100 x \(\frac{3}{25}\) = 12%
![]()
Question 3.
A child friendly bank announces a savings scheme for school children. They will give kiddy banks to children. Children have to keep their savings in it and the bank collects all the money once in a year. To encourage children savings, they give 6% interest if the amount exceeds by ₹ 10000. and other wise 5%. Find the interest received by a school if they deposit is ₹ 9000 for one year.
Solution:
Money deposited = ₹ 9000
Interest applicable 5% on ₹ 9000
= 5 × \(\frac{9000}{100}\) = ₹ 450
Question 4.
A sum of money invested at 8% per annum for simple interest amounts to ₹ 12122 in 2 years. What will it amounts to in 2 year 8 months at 9% rate of interest?
Solution:
First part
Pirnciple = P say
R=8%
T = 2 years
A = ₹ 12,122

Second part
P = ₹10,450
R = 9%
T = 2 years 8 months, A = ?
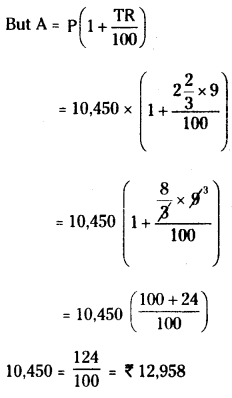
![]()
Question 5.
In 4 years, ₹ 6500 amounts to ₹ 8840 at a certain rate of interest. In what time will ₹ 1600 amounts to 1816 at the same rate?
Solution:
First part
T = 4 years
P = ₹ 6500
A = ₹ 8840
R = R% = ?
I = A – P = 8840 – 6500 = ₹ 2340
But I = \(\frac{P T R}{100}\)
∴ 2340 = \(\frac{6500 \times 4 \times R}{100}\)
∴ R = \(\frac{2340 \times 10 \theta}{6500 \times 4}=\frac{36}{4}\) = 9%
Second part
P = ₹ 1600
A = ₹ 1816
T = ?
R = 9%
I = A – P = 1816 – 1600 = ₹ 216
But I = \(\frac{P T R}{100}\)
∴ 2340 = \(\frac{1600 \times T \times 9}{100}\)
∴ R = \(\frac{216 \times 100 \theta}{1600 \times 9}=\frac{3}{2}\) = 1 \(\frac { 1 }{ 2 }\) years.
