AP State Syllabus AP Board 7th Class Maths Solutions Chapter 5 Triangle and Its Properties Ex 3 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangle and Its Properties Exercise 3
![]()
Question 1.
Find the value of the unknown ‘x’ in the following triangles.
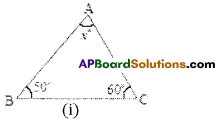
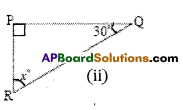
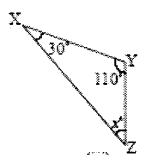
Solution:
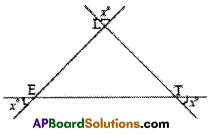
i) In ΔABC

∠A + ∠B + ∠C = 180° (angle sum property
x° + 50° + 60° = 180°
x° + 110° = 180°
x° = 180° – 110°
ii) In ΔPQR,

∠P + ∠Q + ∠R = 180° (angle – sum property)
90° + 30° + x° = 180°
120° + x° – 180°
x° = 180° – 120°
∴ x° = 60°
iii) In ΔXYZ,

∠X + ∠Y + ∠Z = 180° (angle – sum property)
30°+110° + x° =180°
140° + x° = 180°
x° = 180° – 140°
∴ x° = 40°
![]()
Question 2.
Find the values of the unknowns ‘x ‘and ‘y ‘in the following diagrams.
Solution:
i) In ΔPQR,
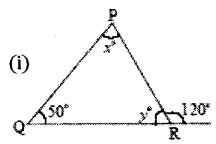
x° + 50° = 120° (exterior angle property)
x°= 120°- 50°
x°= 70°
Also
∠P + ∠Q +∠R = 180° (angle – sum property)
70° + 50° + y° = 180°
120° + y° = 180°
y° = 180° – 120°
y° = 60°
(OR)
y° + 120° = 1800 (linear pair of angles)
y° = 180°- 120°
∴ y° = 60°
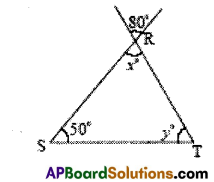
ii) In the figure ΔRST,
x° = 80° (vertically opposite angles)
also ∠R + ∠S + ∠T = 180° (angle – sum property)
80° + 50°+ y°= 180°
130° + y° = 180°
y° = 180° – 130°
∴ y° = 50°
iii) m ΔMAN,
x° = ∠M + ∠A (exterior angle property)
x° = 50° + 60°
x° = 110°
Also x° + y° = 180°
110°+ y°= 180°
y° = 180° – 110°
y° = 70°
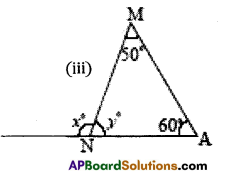
(OR) in ΔMAN,
∠M + ∠A + ∠N = 180° (angle – sum property )
50° + 60° + y° = 180°
110° + y° = 180°
y° = 180°- 110°
∴ y° = 70°
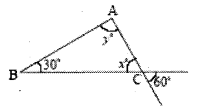
iv) In the figure ΔABC,
x° = 60° (vertically opposite angles)
∠A + ∠B + ∠ACB = 180° (angle – sum property)
y° + 30° + 60° = 180°
y° + 90° = 180°
y° = 180° – 90°
∴ y° = 90°
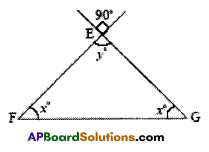
v) In the figure ΔEFG,
y° = 90° (vertically opposite angles)
Also in ΔEFG;
∠F + ∠E + ∠G = 180° (angle – sum property)
∴ x° + x° + y° = 180
2x° + 90° = 180°
2x° = 180°- 90°
2x° = 90°
x° = \(\frac{90^{\circ}}{2}\)
∴ x° = 45°
vi) In the figure ΔLET,
∠L = ∠T = ∠E = x° (vertically opposite angles)
Also in ΔLET
∠L + ∠E + ∠T = 180° (angle – sum property)
x° + x° + x° = 180°
3x° = 180°
x° = \(\frac{180^{\circ}}{3}\)
x° = 60°
![]()
Question 3.
Find the measure of the third angle of triangles whose two angles are given below:
(i) 38° , 102°
(ii) 116°, 30°
(iii) 40°, 80°
Solution:
(i) 38° , 102°
Let the third angle be x° then
38° + 102° + x° = 180° (angle – sum property)
140° + x° = 180°
x° = 180° – 140° = 40°
(ii) 116°, 30°
Let the third angle be x°
then 116° + 300 + x° = 180° (angle – sum property)
146° + x = 180°
x= 180°- 146° = 34°
(iii) 40°, 80°
Let the third angle be x° then
40C + 80° + x° = 180° (angle-sum property)
120°+x° = 180°
x° = 180 – 120° – 60°.
Question 4.
In a right-angled triangle, one acute angle is 30°. Find the other acute angle.
Solution:
Given triangle is right angled triangle.
Let the third angle be x°
then 90° +30° + x° = 180° (angle – sum property)
120° + x° – 180°
x° = 180° – 120° = 60°
![]()
Question 5.
State true or false for each of the following statements.
(i) A triangle can have two right angles.
(ii) A triangle can have two acute angles.
(iii) A triangle can have two obtuse angles.
(iv) Each angle of a triangle can be less than 60°.
Solution:
(i) A triangle can have two right angles. – False
(ii) A triangle can have two acute angles. – True
(iii) A triangle can have two obtuse angles. – False
(iv) Each angle of a triangle can be less than 60°. – False
Question 6.
The angles of a triangle are in the ratio 1 : 2 : 3. Find the angles.
Solution:
Given that ratio of the angle = 1: 2: 3
Sum of the terms of the ratio – 1 + 2 + 3 = 6
Sum of the angles of a triangle = 1800
∴ 1st angle = \(\frac { 1 }{ 6 }\) x 180° = 30° (angle-sum property)
∴ 2nd angle = \(\frac { 2 }{ 6 }\) x 180° = 60° (angle – sum property)
∴ 3rd angle = \(\frac { 3 }{ 6 }\) x 180° = 90° (angIe – sum property)
Question 7.
In the figure, \(\overline{\mathrm{DE}} \| \overline{\mathrm{BC}}\) , ∠A = 300 and ∠B = 50°. Find the values of x, y and z.
Solution:
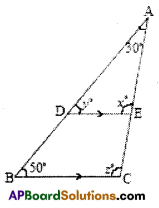
y° = 50° (correspondIng angles)
x° = z° (corresponding angles)
Also in MBC;
∠A + ∠B +∠C = 180° (angIe – sum property)
30° + 50° + z° = 180°
80° + z° = 180°
z° = 180° – 80°
∴ z° = 100°
∴ x° = 100°; y° = 50°; z° = 100°
![]()
Question 8.
In the figure, ∠ABD = 3 ∠DAB and ∠BDC = 96°. Find ∠ABD.
Solution:
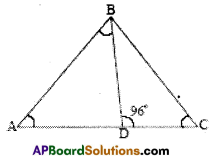
In the figure
∠ABD + ∠DAB = 96° (exterior angle property)
3∠DAB + ∠DAB = 96° (given)
4∠DAB = 96°
∠DAB = \(\frac{96^{\circ}}{4}\) = 24°
∠ABD = 3 x 24° = 72°
Question 9.
In ΔPQR ∠P= 2 ∠Q and 2 ∠R =3 ∠Q , calculate the angles of ΔPQR.
Solution:
In ΔPQR
∠P + ∠Q + ∠R = 180° also
∠P:∠Q:∠R = 2∠Q:∠Q: \(\frac { 3 }{ 2 }\)∠Q = 4 : 2 : 3
Sum of the term of the ratio = 4 + 2 + 3 = 9
∠P = \(\frac { 4 }{ 9 }\) x 180° = 80°
∠Q = \(\frac { 2 }{ 9 }\) x 180° = 40°
∠R = \(\frac { 3 }{ 9 }\) x 180° = 60°
Question 10.
If the angles of a triangle are in the ratio 1:4: 5, find the angles.
Solution:
Given that ratio of the angles = 1 : 4 : 5
Sum of the terms of the ratio = 1 + 4 + 5 = 10
Sum of the angles 180°
∴ 1st angIe = \(\frac { 1 }{ 10 }\) x 180° = 18°
2nd angle \(\frac { 4 }{ 10 }\) x 180° = 72°
3rd angle = \(\frac { 5 }{ 10 }\) x 180°= 90°
![]()
Question 11.
The acute angles of a right triangle are in the ratio 2 : 3. Find the angles of the triangle.
Solution:
Given that ratio of acute angles = 2 : 3
Sum of the terms of the ratio = 2 + 3 = 5
Sum of the acute angles = 90°
∴ 1st acute angle x 900 = 36°
2nd acute angle = x 900 = 540
∴ Angles of the triangle = 36°, 54° and 90°
Question 12.
In the figure, ∆PQR is right angled at Q, \(\overline{\mathrm{ML}} \| \overrightarrow{\mathrm{RQ}}\) and ∠LMR = 130°. Find ∠LPM, ∠PML and ∠PRQ.
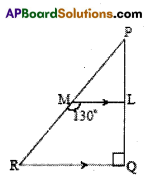
Solution:
∠PRQ + ∠LMR = 180° (int, angles on the same side of the transversal)
∠PRQ + 130° = 18 0°
∴ ∠PRQ = 180° – 130°= 50°
In ∆PRQ,
∠P + ∠R +∠Q = 180° (angle – sum property)
∠LPM + 50° + 90° = 180°
∠LPM + 140° = 180°
∴ ∠LPM = 180° – 140° = 40°
Also ∠PML + ∠LMR = 180° (Linear pair of angles)
∴ ∠PML + 130° = 180°
∠PML = 180° – 130° = 50°
(or) ∠PML = ∠PRQ = 50° (corresponding angles)
![]()
Question 13.
In Figure ABCDE, find ∠1 +∠2 + ∠3 + ∠4 + ∠5.
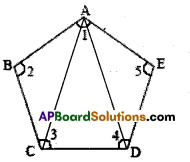
Solution:
In ∆ABC, ∠BAC + ∠ACB + ∠ABC = 180° ………….(1)
In ∆ACD, ∠CAD + ∠ADC + ∠ACD = 180° ……………. (2)
In ∆ADE, ∠DAE + ∠ADE + ∠AED = 180° …………(3)
Adding (1), (2) and (3) we get
(∠BAC + ∠ACB + ∠ABC) + ∠CAD+ (∠ADC + ∠ACD + ∠DAE + ∠ADE + ∠AED = 180°+ 180° 180°
(∠BAC + ∠CAD + ∠DAE) + ∠ABC + (∠ACB + ∠ACD) + ∠ADC + ∠ADE) + ∠AED = 180° + 180° + 180°
Hene
∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 540°
