AP State Syllabus AP Board 7th Class Maths Solutions Chapter 2 Fractions, Decimals and Rational Numbers Ex 1 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 2nd Lesson Fractions, Decimals and Rational Numbers Exercise 1
![]()
Question 1.
Solve the following.
(i) 2 + \(\frac { 3 }{ 4 }\)
(ii) \(\frac{7}{9}+\frac{1}{3}\)
(iii) 1 – \(\frac{4}{7}\)
(iv) \(2 \frac{2}{3}+\frac{1}{2}\)
(v) \(\frac{5}{8}-\frac{1}{6}\)
(vi) \(2 \frac{2}{3}+3 \frac{1}{2}\)
Solution:

Question 2.
Arrange the following in ascending order.
(i) \(\frac{5}{8}, \frac{5}{6}, \frac{1}{2}\)
(ii) \(\frac{2}{5}, \frac{1}{3}, \frac{3}{10}\)
Solution:

Question 3.
Check whether in this square the sum of the numbers in each row and in each column and along the diagonals is the same.

Solution:

Question 4.
A rectangular sheet of paper is 5\(\frac{2}{3}\) cm long and 3\(\frac{1}{5}\) cm wide. Find its perimeter.
Solution:
Length of the rectangular sheet = 5\(\frac{2}{3}\) cm
Breadth/width of the rectangular sheet = 5\(\frac{2}{3}\) cm
Perimeter = 2 x (length + breadth)

Question 5.
The recipe requires 3\(\frac{1}{4}\) cups of flour. Radha has 1\( \frac{3}{8}\) cups of flour. How many more cups of flour does she need?
Solution:
Flour required for the recipe = 3\(\frac{1}{4}\) cups
Flour with Radha = 1\(\frac{3}{8}\) cups
More cups of flour required = \(3 \frac{1}{4}-1 \frac{3}{8}\)
= \(\frac{3 \times 4+1}{4}-\frac{1 \times 8+3}{8}\)

Question 6.
Abdul is preparing for his final exam. He has completed \(\frac{5}{12}\) part of his course content. Find out how much course content is left?
Solution:
Take content as 1 (i.e., full) Course completed = \(\frac{5}{12}\)
Course yet to be completed = 1 – \(\frac{5}{12}\)
= \(\frac{12 \times 1-5}{12}\)
\(\frac{12-5}{12}=\frac{7}{12}\)
Question 7.
Find the perimeters of(i) ΔABE (ii) the rectangle BCDE in this figure. Which figure has greater perimetre and by how much?
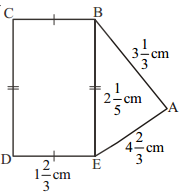
Solution:
i) Perimeter of ΔABE = AB + BE + AE
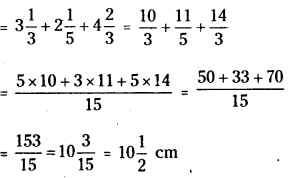
ii) Perimeter of BCDE = 2(BE + BC)
![]()
As \(\frac{116}{15}<\frac{153}{15}\), we conclude that the perimetre of ΔABE > Perimeter of BCDE
