AP State Syllabus AP Board 7th Class Maths Solutions Chapter 11 Exponents InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 11th Lesson Exponents InText Questions
![]()
Do This
Question 1.
Write the following in exponential form, (values are rounded off) (Page No. 212)
i) Total surface area of the Earth is 510,000,000 square kilometers.
Solution:
51 × 107 = 3× 17 × 107
ii) Population of Rajasthan is approximately 7,00,00,000.
Solution:
7 × 107
iii) The approximate age of the Earth is 4550 million years.
Solution:
4550 millions = 4550 × 10,00,000 (v 1 million =10 lakhs)
= 455 × 107 = 91 × 5 × 107 = 5 × 7 × 13 × 107
iv) 1000 km in meters.
Solution:
1 km = 1000 m
∴ 1000 km = 1000 × 1000 m = 106
![]()
Question 2.
Express (i) 48951 (ii) 89325 in expanded form using exponents. (Page No. 212)
Solution:
i) 48951 = (4 × 10000) + (8 × 1000) + (9 × 100) + (5 × 10) + (1 × 1)
= (4 × 104) + (8× 103) + (9 × 102) + (5 × 1.0) + (1 × 1)
ii) 89325 = (8 × 10000) + (9 × 1000) + (3 × 100) + (2 × 10) + (5 × 1)
= (8 × 104) + (9 × 103) + (3 × 102) + (2 × 10) + (5 × 1)
Question 3.
Is 32 equal to 23 ? Justify. (Page No. 213)
Solution:
32 ≠ 23
Since 32 = 3 × 3 = 9 and 23 = 8
∴ 32 ≠ 23
Question 4.
Write the following numbers in exponential form. Also state the
a) base b) exponent and c) how it is read.
i) 32 ii) 64 iii) 256 iv) 243 v) 49 (Page No. 213)
Solution:
i) 32 = 2 × 2 × 2 × 2 × 2 = 25
Base = 2; exponent = 5; read as 2 raised to the power 5.
ii) 64 = 2 × 2× 2 × 2 × 2 × 2 = 26
Base = 2; exponent = 6 and we read it as 2 raised to the power 6.
iii) 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 28
Base = 2, exponent = 8 and we read it as 2 raised to the power 8.
iv) 243 = 3 × 3 × 3 × 3 × 3 = 35
Base = 3; exponent = 5 and we read it as 3 raised to the power 5.
v) 49 = 7 × 7 = 72
= 7 is the base ; exponent = 2.
![]()
Question 5.
Write the expanded form of the following. (Page No. 213)
i) p7 ii) l4 iii) s9 iv) d6 v) z5
Solution:
i) p7 = p × p × p × p × p × p × p
ii) l4 = l × l × l × l
iii) s9 = s × s × s × s × s × s × s × s × s
iv) d6 = d × d × d × d × d × d
v) z5 = z × z × z × z × z
Question 6.
Write the following in exponential form. (Page No. 213)
i) a × a × a × ………………….l’ times
ii) 5 × 5 × 5 × 5 × ……………..’n’ times
iii) q × q × q × q × q ………………….15 times
iv) r × r × r × ………………….’b’ times
Solution:
i) a × a × a × ………………….’l’ times = al
ii) 5 × 5 × 5 × 5 × ……………..’n’ times = 5n
iii) q × q × q × q × q …………….15 times = q15
iv) r × r × r × ……………..’b’ times = rb
Do This
Question 1.
Find the values of 24, 23 and 27 and verify whether 24 × 23 = 27. (Page No. 215)
24 = 2 × 2 × 2 ×2 = 16;
23 = 2 × 2 x 2 = 8
27 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
24 × 23 = 16 × 8 = 128 = 27
24 × 23 = 27
Question 2.
Find the values of 52, 53 and 55 and verify whether 52 × 53 = 55. (Page No. 215)
Solution:
52 = 5 × 5 = 25;
53 = 5 × 5 × 5 = 125 and 55 = 5 × 5 × 5 × 5 × 5 = 3125
Now 52 × 53 = 25 × 125 = 3125 = 55
∴ 52 × 53 = 55
![]()
Question 3.
Simplify the following using the formula am × an = am + n (Page No. 216)
i) 311 × 39 ii) p5 × p8
Solution:
i) 311 × 39 = 311+9 = 320
ii) p5 × p8 = p5+8 = p13
Question 4.
Find the appropriate number in place of the symbol’?’in the following. (Page No. 216)
Let ‘k’ be any non-zero integer.
i) k3 × k4 = k?
Solution:
i) k3 × k4 = k?
as k3 × k4 = k3+4 = k7 the value of ‘?’ = 7
ii) k15 × k? = k31
as k15 × k? = k15+?
but k15 + ? = k31
Since bases are equal we equate the exponents
∴ 15 + ? = 31
(i.e„) ? = 31 – 15 = 16
![]()
Question 5.
Compute 36, cube of 32 and verify whether (32)3 = 36. (Page No. 216)
Solution:
36 = 3 × 3 × 3 × 3 × 3 × 3 = 729.
cube of 32 = (32)3 = 93 = 9 × 9 × 9 = 729
Now (32)3 = 32 × 32 × 32 = 9 × 9 × 9 = 729
36 = 3 × 3 × 3 × 3 × 3 × 3 = 9 × 9 × 9
(32)3 = 36
Question 6.
Simplify the following using the law am × bm = (ab)m (Page No. 218)
i) (2 × 3)4
ii) xp × yp
iii) a8 × b8
iv) (5 × 4)11
Solultion:
i) (2 × 3)4 = 24 × 3 4 = (2 × 2 × 2 × 2) × (3 × 3 × 3 ×3) = 16 × 81 = 1296
ii) xp × yp = (x . y)p
iii) a8 × b8 = (a.b)8
iv) (5 × 4)11 = 511 × 411 = 511 × (2 × 2)11
= 511 × 211 × 211 = (5 × 2)11 × 211 = 1011 × 211
![]()
Question 7.
Write the following, by using \(\mathbf{a}^{-n}=\frac{1}{\mathbf{a}^{n}}\) with positive exponents. (Page No. 219)
Solution:
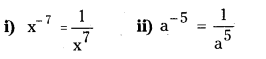

Question 8.
Simplify and write in the form of am-n or \(\frac{1}{\mathbf{a}^{\mathbf{n}-\mathbf{m}}}\)
i) \(\frac{13^{8}}{13^{5}}\)
ii) \(\frac{3^{4}}{3^{14}}\)
Solution:

![]()
Question 9.
Fill the appropriate number in the box. (Page No. 222)
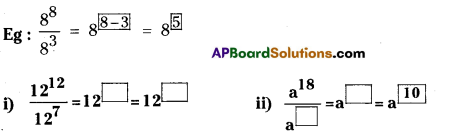
Solution:

Question 10.
Complete the following (Page No. 223)
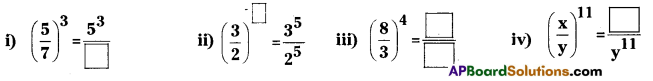
Solution:
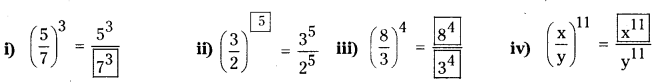
Question 11.
Write in expanded form. (Page No. 224)
i) a-5
ii) (-a)4
iii) (-7)-5
iv) (-a)m
Solution:
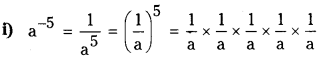

![]()
Question 12.
Write in exponential form. (Page No. 224)
i) (-3) × (-3) × (-3)
ii) (-b) × (-b) × (-b) × (-b)
iii) \(\left(\frac{1}{-2}\right) \times\left(\frac{1}{-2}\right) \times\left(\frac{1}{-2}\right)\) ………………….’m’ times
Solution:
i) (-3) × (-3) × (-3) = (-3)3
ii) (-b) × (-b) × (-b) × (-b) = (-b)4
iii) \(\left(\frac{1}{-2}\right) \times\left(\frac{1}{-2}\right) \times\left(\frac{1}{-2}\right)\) ………………….’m’ times = \(\left(-\frac{1}{2}\right)^{m}\) or (-2)-m
Do This
Question 1.
Write the following in exponential form using prime factorization. (Page – 214)
i) 2500 ii) 1296 iii) 8000 iv)6300
Solution:
i) 2500 = 2 × 1250 = 2 × 2 × 625
= (2 × 2) × 5 × 125
= (2 × 2) × 5 × 5 × 25
= (2 × 2) × (5 × 5 × 5 × 5)
= 22 × 54

ii) 1296 = 2 × 648 = 2 × 2 × 324 = 2 × 2 × 2 × 162
= (2 × 2 × 2 × 2) × 81
= (2 × 2 × 2 × 2 ) × 3 × 27
= (2 × 2 × 2 × 2 ) × 3 × 3 × 9
= (2 × 2 × 2 × 2 ) × ( 3 × 3 × 3 × 3 )
= 24 × 34
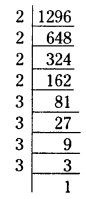
iii) 8000 = 2 × 4000 = 2 × 2 × 2000 = 2 × 2 × 2 × 1000
= 2 × 2 × 2 × 2 × 500
= 2 × 2 × 2 × 2 × 2 × 250
= (2 × 2 × 2 × 2 × 2 × 2) × 125
= (2 × 2 × 2 × 2 × 2 × 2) × 5 × 25
= (2 × 2 × 2 × 2 × 2 × 2) × ( 5 × 5 × 5)
= (26 × 53)

![]()
iv) 6300 = 2 × 3150 = 2 × 2 × 1575
= (2 × 2) × 3 × 525
= 2 × 2 × 3 × 3 × 175
= (2 × 2) × (3 × 3) × 5 × 35
= (2 × 2) × (3 × 3) × (5 × 5) × 7
= 22 × 32 × 52 × 7

