AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 1 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 1
![]()
Question 1.
Find the rule which gives the number of matchsticks required to make the following patterns
(i) A pattern of letter ‘H’
(ii) A pattern of letter ‘V’
Solution:
i) A pattern of letter ‘H’
The letter ‘H’ is formed with 3 matchsticks.
∴ Its pattern should be 3, 6, 9, 12 (or)
3 × 1, 3 × 2, 3 × 3, 3 × 4 ……………….. 3 x n
∴ The required pattern is 3 × n = 3n
ii) A pattern of letter ‘V’
The letter ‘V’ is formed with 2 matchsticks.
∴ Its pattern should be 2, 4. 6. 8 (or)
2 × 1, 2 × 2, 2 × 3 …………………2 × n
∴ The required pattern is 2 × n = 2n
![]()
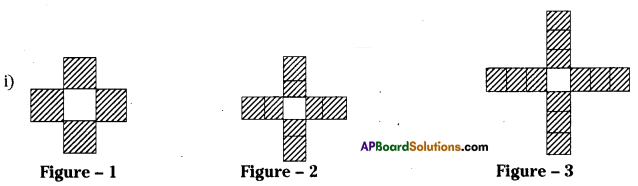
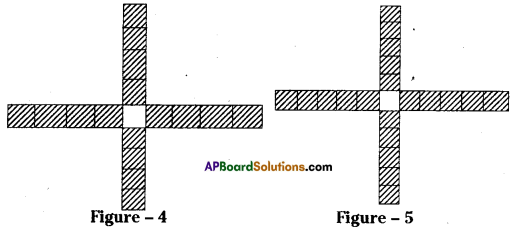
Question 2.
Given below is a pattern made from coloured tiles and white tiles.

(i) Draw the next two figures in the pattern above.
(ii) Fill the table given below and express the pattern in the form of an algebraic expression.

(iii) Fill the table given below and express the pattern in the form of an algebraic expression.
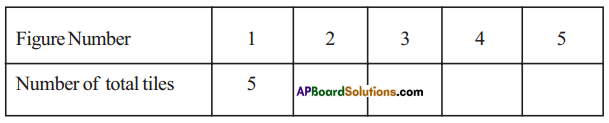
Solution:

∴ The required algebraic expression is “4”

∴ The required algebraic expression is “4+1”
If n = 1 ⇒ 4n + 1 = 4(1) + 1 = 5
n = 2 ⇒ 4 × 2 + 1 = 8 + 1 = 9
n = 3 ⇒ 4 × 3 + 1 = 12 + 1 =13 ……………….. soon.
![]()
Question 3.
Write the following statements using variables, constants and arithmetic operations.
(i) 6 more than p
(ii) ‘x’ is reduced by 4
(iii) 8 subtracted from y
(iv) q multiplied by ‘-5’
(v) y divided by 4
(vi) One-fourth of the product of ’p’ and ‘q’
(vii) 5 added to the three times of ’z’
(viii) x multiplied by 5 and added to ‘10’
(ix) 5 subtracted from two times of ‘y’
(x) y multiplied by 10 and added to 13
Solution:
| Sentence | Algebraic expression |
| 1. 6 more than p | p + 6 |
| 2. x is reduced by 4 | x – 4 |
| 3. 8 subtracted from y | y – 8 |
| 4. q multiplied by ‘-5’ | -5q |
| 5. y divided by 4 | \(\frac{y}{4}\) |
| 6. One-fourth of the product of ‘p’ and ‘q’ | \(\frac{\mathrm{pq}}{4}\) |
| 7. 5 added to the three times of z | 3z + 5 |
| 8. ‘x’ multiplied by 5 and added to 10 | 5x + 10 |
| 9. 5 subtracted from two times of ‘y’ | 2y – 5 |
| 10. y multiplied by 10 and added to 13 | 10y + 13 |
![]()
Question 4.
Write the following expressions in Statements.
(i) x + 3
(ii) y – 7
(iii) 10l
(iv) \(\frac{x}{5}\)
(v) 3m + 11
(vi) 2y – 5
Solution:
Expression Statements
| Expression | Statements |
| i) x + 3 | x is added to 3 |
| ii) y – 7 | 7 is subtracted from y. |
| iii) 10l | l is multiplied by 10. |
| iv) \(\frac{\mathrm{x}}{5}\) | x is divided by 5 |
| v) 3m + 11 | m is multiplied by 3 and added to 11 |
| vi) 2y – 5 | y is multiplied by 2 and 5 ¡s subtracted from the product |
![]()
Question 5.
Some situations are given below. State the number in situations is a variable or constant?
Example: Our age – its value keeps on changing so it is an example of a variable quantity.
(i) The number of days in the month of January
(ii) The temperature of a day
(iii) Length of your classroom
(iv) Height of the growing plant
Solution:
i) No. of days ¡n the month of January are fixed in every year. So, “Number of days” is a constant.
ii) The temperature of a day changes every minute. So (temperature) it ¡s a variable.
iii) The length of the classroom is fixed. So it is a constant.
iv) The height of a growing plant changes in every month. So it is a variable.
