AP Board 10th Class Maths Solutions Chapter 2 సమితులు InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 2 సమితులు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 2nd Lesson సమితులు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
కింద ఇవ్వబడిన ప్రతి దంతాల రకం యొక్క జాబితాను తయారుచేయండి. (పేజీ నెం.25)

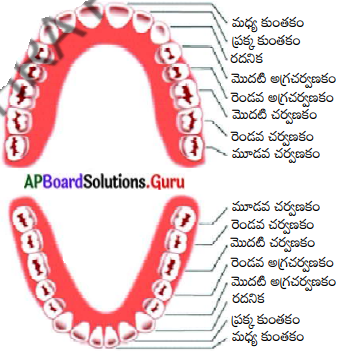
(i) కుంతకాలు
సాధన.
(ప్రక్క, కుంతకం, మధ్య కుంతకం) (ఎడమ, కుడి, పై, కింద).

(ii) రదనికలు
సాధన.
(ఎడమ కింది రదనిక, ఎడమ పై రదనిక, కుడి కింది” రదనిక, కుడి పై రదనిక)

(iii) అగ్రచర్వణకాలు
సాధన.
(ఎడమ అగ్ర చర్వణకం, ఎడమ కింది అగ్రచర్వణకం, కుడిపై అగ్ర చర్వణకం, ఎడమ రెండవ కింది చర్వణకం, ఎడమ రెండవపై అగ్రచర్వణకం).

(iv) చర్వణకాలు
సాధన.
మొదటి ఎడమపై చర్వణకం, మొదటి కింది ఎడమ చర్వణకం,
రెండవ ఎడమపై చర్వణకం, రెండవ కింది ఎడమ చర్వణకం,
మూడవ ఎడమపై చర్వణకం, మూడవ కింది ఎడమ చర్వణకం,
రెండవ కుడిపై చర్వణకం, రెండవ కుడి కింది చర్వణకం,
మూడవ కుడిపై చర్వణకం, మూడవ కుడి కింద చర్వణకం.

ప్రశ్న 2.
ఈ కింది సముదాయాలలోని సామాన్య ధర్మాన్ని గుర్తించి రాయండి. (పేజీ నెం.26)

1. 2, 4, 6, 8, ……. . .
సాధన.
ఇవి అన్ని సరి సంఖ్యలు

2.
2, 3, 5, 7, 11, …………
సాధన.
ఇవి అన్ని ప్రధాన సంఖ్యలు

3. 1, 4, 9, 16, …………
సాధన.
ఇవి అన్ని ఖచ్చిత వర్గ సంఖ్యలు

4. జనవరి, ఫిబ్రవరి, మార్చి, ఏప్రిల్, ……………
సాధన.
ఇవి ఒక సంవత్సరంలో ఉండే నెలల ఆంగ్ల, పేర్లు.

5. బొటనవేలు, చూపుడువేలు, మధ్యవేలు, ఉంగరపు వేలు, చిటికనవేలు.
సాధన.
ఇవి ఒక వ్యక్తి వేళ్ళ పేర్లు.

ప్రశ్న 3.
ఈ క్రింది సమితులను రాయండి… (పేజీ నెం. 27)

1) మొదటి ఐదు ధన పూర్ణ సంఖ్యల సమితి
సాధన.
A = {1, 2, 3, 4, 5}

2) 100 కంటే ఎక్కువ 125 కంటే తక్కువైన 5 యొక్క గుణిజాల సమితి
సాధన.
B = {105, 110, 115, 120}

3) మొదటి 5 ఘన సంఖ్యల సమితి
సాధన.
C = {1, 8, 27, 64, 125} .
4) రామానుజన్ సంఖ్యలోని అంకెల సమితి.
సాధన.
D = {1, 2, 7, 9}

ప్రశ్న 4.
ఈ కింది సంఖ్యలు ఏ సంఖ్యాసమితికి చెందుతాయో? – చెందవో ? నిర్ణయించి, సరియైన గుర్తుతో వ్యక్తపరచండి. (పేజీ నెం. 28)
(i) 1
సాధన.
1 ∈ N, 1 ∉ Q

(ii) 0
సాధన.
0 ∈ W, 0 ∉ N

(iii) -4
సాధన.
-4 ∈ Z, – 4 ∉ N

(iv) \(\frac{5}{6}\)
సాధన.
\(\frac{5}{6}\) ∈ Q, \(\frac{5}{6}\) ∉ N

(v) \(1 . \overline{3}\)
సాధన.
\(1 . \overline{3}\) ∈ Q, \(1 . \overline{3}\) ∉ Q’

(vi) √2
సాధన.
√2 ∈ Q’, √2 ∉ W

(vii) log 2
సాధన.
log 2 ∈ Q’, log 2 ∉ Z

(viii) 0.03
సాధన.
0.03 ∈ Q; 0.03 ∉ Q’

(ix) π
సాధన.
π∈ R, π ∉ N

(x) \(\sqrt{-4}\)
సాధన.
\(\sqrt{-4}\) ∈ i; \(\sqrt{-4}\) ∉ W.

ప్రశ్న 5.
కింది సమితులలోని మూలకాల జాబితాను రాయండి.
(i) G అనేది 20 కు రాయగల కారణాంకాలన్నింటిని కలిగిన సమితి.
(ii) F అనేది 17 మరియు 61 మధ్యగల 4 యొక్క గుణిజాలు మరియు 7చే భాగించబడే మూలకాల సమితి.
(iii) S = {x: X అనేది ‘MADAM’ అనే పదంలో గల అక్షరాల సమితి}
(iv)P = {x: X అనేది 3.5 మరియు 6.7 మధ్యగల పూర్ణాంకాల సమితి} (పేజీ నెం. 29)
సాధన.
(i) G = {1, 2, 4, 5, 10, 20}
(ii) F = {28, 56}
(iii) S = {M, A, D}
(iv) P = {4, 5, 6}

ప్రశ్న 6.
క్రింది సమితులను రోస్టర్ రూపంలో రాయండి.
(i) B అనేది ఒక సంవత్సరంలో ఒక నెలకి 30 రోజులుగా గల అన్ని నెలల సమితి.
(ii) P అనేది 10 కంటే తక్కువైన అన్ని ప్రధాన , సంఖ్యల సమితి.
(iii) X అనేది ఇంద్రధనుస్సులో గల అన్ని రంగుల సమితి. (పేజీ నెం. 29)
సాధన.
(i) B = {ఏప్రిల్, జూన్, సెప్టెంబర్, నవంబర్ }
(ii) P = {2, 3, 5, 7}
(iii) {ఊదా, ముదురు నీలం, నీలం, ఆకుపచ్చ, పసుపు, నారింజ, ఎరుపు} (లేదా) {Violet, Indigo, Blue, Green, Yellow, Orange, Red}

ప్రశ్న 7.
A అనేది 12కు కారణాంకాలుగా గల సమితి. ఈ క్రింది వానిలో ఏది ‘A’ సమితికి చెందదు? (పేజీ నెం. 29)
(A) 1
(B) 4
(C) 5
(D) 12
సాధన.
[C]

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
క్రింది సముదాయాలను పరిశీలించి, వాటి ధర్మాలను తెలిపే మరికొన్ని ‘సాధారణ ప్రవచనాలను’ రాయండి. (పేజీ నెం. 27)
(i) 2, 4, 6, 8, ……….
సాధన.
a) ఇవి అన్ని సరి సహజ సంఖ్యలు.
b) ఇవి అన్ని రెండు యొక్క గుణిజాలు.
C) ఇవి రెండు సామాన్య భేదంగాను, రెండు మొదటి పదంగాను గల అంకశ్రేఢిలోని పదాలు. ,
d) ఇవి అన్ని బేసి సంఖ్యలు కాని సహజ సంఖ్యలు.

(ii) 1, 4, 9, 16…..
సాధన.
a) ఇవి వరుస సహజ సంఖ్యల వర్గాలు.
b) వీని మధ్య భేదం ఒక అంకశ్రేణి a = 3, d = 2.

ప్రశ్న 2.
అకరణీయ సంఖ్యా సమితి (Q) ని, దానిలోని మూలకాలచే ‘ జాబితారూపం’లో సూచించగలరా ? (పేజీ నెం. 28)
సాధన.
అకరణీయ సంఖ్యా సమితిని జాబితా రూపంలో సూచించలేము. ఎందుకనగా ఇందులో అపరిమిత సంఖ్యలో మూలకాలుంటాయి గనుక దీనిని జాబితా రూపంలో వ్రాయలేము.

ప్రయత్నించండి:

ప్రశ్న 1.
బీజగణిత మరియు రేఖాగణిత భావనలతో కొన్ని సమితులను ఏర్పరచండి. (పేజీ నెం. 30)
సాధన.
(i) A = {x : x² – 25 = 0 మరియు x ∈ Z}
(ii) B = {x : x = \(\frac{y}{y+1}\), y ∈ W మరియు y < 7}
(iii) C = {x : 3x – 2 < 15 మరియు x ∈ W}
(iv) D = {అల్పకోణ త్రిభుజం, లంబకోణ త్రిభుజం, అధిక కోణ త్రిభుజం}
(v) E = {కర్ణాలు లంబసమద్విఖండనం చేసుకొనే చతుర్భుజాలు}
(vi) F = {x = 3 సరళరేఖకు సమాంతరంగా గల రేఖల సమితి}
(vii) G = {అంతర కోణాల మొత్తం 360° గా గల బహుభుజుల సమితి}.

ప్రశ్న 2.
రోస్టర్ రూపంతో, సమితీ నిర్మాణ రూపంను జతపరచండి.

సాధన.
(i) d
(ii) c
(iii) a
(iv) b

ఇవి చేయండి:

ప్రశ్న 1.
A = {1, 2, 3, 4}, B = {2, 4}, C = {1, 2, 3, 4, 7}, F = { } అయిన క్రింది ఖాళీలను ⊂ లేదా ⊄ లతో పూరించండి. (పేజీ నెం. 34)
(i) A …… B
సాధన.
A ⊄ B

(ii) C ……. A
సాధన.
C ⊄ A

(iii) B …… A
సాధన.
B ⊂ A

(iv) A …… C
సాధన.
A ⊂ C

(v) B …… C
సాధన.
B ⊂ C

(vi) Φ …… B
సాధన.
Φ ⊂ B

ప్రశ్న 2.
క్రింది వాక్యాలలో ‘సత్యమైన’ వాటిని పేర్కొనండి. ((పేజీ నెం. 34)
(i) { } = Φ
సాధన.
సత్యం

(ii) Φ = 0
సాధన.
అసత్యం

(iii) 0 = {0}
సాధన.
అసత్యం

ప్రశ్న 3.
A = {1, 3, 7, 8} మరియు B = {2, 4, 7, 9} అయిన A ∩ B కనుక్కోండి. (పేజీ నెం. 38)
సాధన.
A = { 1, 3, 7, 8}, B = {2, 4, 7, 9}
∴ A ∩ B = {7}.

ప్రశ్న 4.
A = {6, 9, 11}; B = { } అయిన A ∪ Φ కనుక్కొండి. (పేజీ నెం. 38)
సాధన.
A ∪ Φ = {6, 9, 11} ∪ { } = {6, 9, 11}
A ∪ Φ = A

ప్రశ్న 5.
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; B = {2, 3, 5, 7}. A ∩ B కనుగొని, A ∩ B = B అని చూపండి. (పేజీ నెం. 38)
సాధన.
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, B = {2, 3, 5, 7}
A ∩ B = {2, 3, 5, 7}
⇒ A ∩ B = B

ప్రశ్న 6.
A = {4, 5, 6}; B = {7, 8} అయిన A ∪ B = B ∪ A అని చూపండి. (పేజీ నెం. 38)
సాధన.
A ∪ B = {4, 5, 6} ∪ {7, 8} = {4, 5, 6, 7, 8}
B ∪ A= {7, 8} U {4, 5, 6} = {4, 5, 6, 7, 8}
∴ A ∪ B = B ∪ A

ప్రశ్న 7.
A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7} అయిన A – B మరియు B – A కనుగొనండి. A- B, B – A లు రెండు సమానమా? (పేజీ నెం. 39)
సాధన.
A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7}
A – B = {1, 2, 3, 4, 5} {4, 5, 6, 7} = {1, 2, 3}
B – A = {4, 5, 6, 7} {1, 2, 3, 4, 5} = { 6, 7}
A – B ≠ B – A

2వ పద్దతి :
వెన్ చిత్రం ద్వారా A – B, B – A ను కనుగొనడం

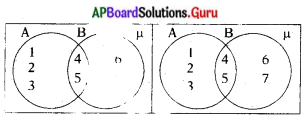
B – A = {6, 7}
A – B = {1 2, 3}
A – B ≠ B – A

ప్రశ్న 8.
V = {a, e, i, 0, U} మరియు B = {a, i, k, u} – అయిన V – B మరియు B – V లను కనుగొనండి. (పేజీ నెం. 39)
సాధన.
V = {a, e, i, 0, u}; B = {a, i, k, u}
V – B = {a, e, i, 0, u} – {a, i, k, u} = {e, o}
B – V = {a, i, k, u} – {a, e, 1, 0, u} = {k}

2వ పద్ధతి :
వెన్ చిత్రం ద్వారా

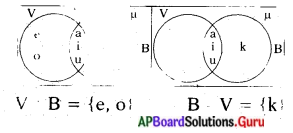
ప్రయత్నించండి:

ప్రశ్న 1.
A = {చతుర్భుజాలు}, B = {చతురస్రం, దీర్ఘచతురస్రం, ట్రెపీజియం , రాంబస్}. A ⊂ B లేక B ⊂ A అవుతుందేమో పేర్కొనండి. నీ సమాధానాన్ని సమర్థించండి. (పేజీ నెం. 34)
సాధన.
A = {చతుర్భుజాలు}
B = {చతురస్రం, దీర్ఘచతురస్రం. ట్రెపీజియం, రాంబస్ }

(i) A ⊄ B చతుర్భుజాల సమితి A లో సమాంతర చతుర్భుజం ఉంటుంది. కాని B సమితిలో సమాంతర చతుర్భుజం లేదు. కావున A ⊄ B.
(ii) B ⊂ A
B సమితిలోని మూలకాలైన చతురస్రం, దీర్ఘచతురస్రం, ట్రెపీజియం, రాంబన్లు అన్నీ చతుర్భుజాలే అనగా A B లోని మూలకాలన్నీ A లో ఉన్నాయి. కాబట్టి B ⊂ A.

ప్రశ్న 2.
A = {a, b, c, d} అయిన Aకి ఎన్ని — — ఉపసమితులున్నాయి? (పేజీ నెం. 34)
(A) 5
(B) 6
(C) 16
(D) 65
సాధన.
Hint: n మూలకాలు కలిగిన సమితికి గల ఉపసమితుల సంఖ్య 2ⁿ.
జవాబు : [C].

ప్రశ్న 3.
P అనేది 5 యొక్క కారణాంకాల సమితి. Q అనేది 25 యొక్క కారణాంకాల సమితి. R అనేది 125 యొక్క కారణాంకాల సమితి. క్రింది వానిలో ఏది అసత్యం ? (పేజీ నెం. 34)
(A) P ⊂ Q
(B) Q ⊂ R
(C) R ⊂ P
(D) T ⊂ R
సాధన.
Hint : P = {1, 5} Q = {1, 5, 25) R = {1, 5, 25, 125}
జవాబు : [C].

ప్రశ్న 4.
A అనేది 10 కంటే తక్కువైన ప్రధానాంకాల సమితి, B అనేది 10 కంటే తక్కువైన బేసి సంఖ్యల సమితి. C అనేది 10 కంటే తక్కువైన సరిసంఖ్యల సమితి. క్రింది వానిలో ‘సత్యమైన” వాక్యా లేవి ? (పేజీ నెం. 34)
(i) A ⊂ B
(ii) B ⊂ A
(iii) A ⊂ C
(iv) C ⊂ A
(v) B ⊂ C
(vi) Φ ⊂ A
సాధన.
A = {2, 3, 5, 7} B = {1, 3, 5, 7, 9} C = {2, 4, 6, 8}
(i) A ⊂ B అసత్యం
(ii) B ⊂ A అసత్యం
(iii) A ⊂ C అసత్యం
(iv) C ⊂ A అసత్యం
(v) B ⊂ C అసత్యం
(vi) Φ ⊂ A సత్యం

ప్రశ్న 5.
A మరియు B వియుక్త సమితులు అయ్యేటట్లుగా కొన్ని సమితులు A మరియు B లు, వాని మూలకాలు ఎన్నుకొని జాబితా తయారుచేయండి. (పేజీ నెం. 38)
సాధన.
A మరియు B లు వియుక్త సమితులు అయ్యేటట్లు A, B లకు కొన్ని ఉదాహరణలు.
ఉదా 1: A = {1, 3, 5, 7, 9} B = {2, 4, 6, 8, 10}
ఉదా 2: A = {1, 3, 7, 21} B = {2, 4, 5, 8, 10, 20 40}
ఉదా 3: A = {1, 2, 3, 4, 5 6} B = {7 8 9 10}

ప్రశ్న 6.
A = {2, 3, 5} అయిన A ∪ Φ మరియు Φ ∪ A కనుగొని పోల్చండి. (పేజీ నెం. 38)
సాధన.
A = {2, 3, 5}
A ∪ Φ = {2, 3, 5} ∪ { } = {2, 3, 5}
Φ ∪ A = { } ∪ {2, 3, 5} = {2, 3, 5}
∴ A ∪ Φ = Φ ∪ A = A

ప్రశ్న 7.
A = {1, 2, 3, 4}; B = {1, 2, 3, 4, 5, 6, 7, 8} అయిన A ∪ B, A ∩ B కనుగొనండి. ఫలితం నుండి మీరు ఏమి గమనించారు ? (పేజీ నెం. 38)
సాధన.
A = {1, 2, 3, 4} B = {1, 2, 3, 4, 5, 6, 7, 8}
(i) A ∪ B = {1, 2, 3, 4} ∪ {1, 2, 3, 4, 5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}
A ⊂ B ⇒ A ∪ B = B

(ii) A ∩ B = {1, 2, 3, 4} ∩ {1, 2, 3, 4, 5, 6, 7, 8} = {1, 2, 3, 4}
A ⊂ B ⇒ A ∩ B = A మరియు A ∪ B ≠A ∩ B.

ప్రశ్న 8.
A = {1, 2, 3, 4, 5, 6}; B = {2, 4, 6, 8, 10} గా ఇవ్వబడినవి. A, B ల ఛేదనాన్ని కనుగొనండి.(పేజీ నెం. 38)
సాధన.
A = {1, 2, 3, 4, 5, 6}
B = {2, 4, 6, 8, 10} A, B ల ఛేదనము
A ∩ B = {1, 2, 3, 4, 5, 6} ∩ {2, 4, 6, 8, 10} = {2, 4, 6}

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
ఏవైనా రెండు వియుక్త సమితుల ఛేదనం శూన్య సమితి అవుతుంది. ఈ వాక్యం సత్యమా ? అసత్యమా? (పేజీ నెం. 38)
సాధన.
సత్యం. వియుక్త సమితులలో ఉమ్మడి మూలకాలు ఉండవు కాబట్టి వియుక్త సమితుల ఛేదనం శూన్యసమితి.

ప్రశ్న 2.
సమితులు A – B, B – A మరియు A ∩ B పరస్పరం వియుక్త సమితులు అవుతాయి. కొన్ని ఉదాహరణల సహాయంతో ఈ సత్యాన్ని పరిశీలించండి. (పేజీ నెం. 39)
సాధన.
ఉదా 1 :
A = {1, 2, 3, 5, 8} B = {1, 2, 4, 6, 8, 10} అనుకుందాం .
A – B = {1, 2, 3, 5, 8} – {1, 2, 4, 6, 8, 10} = {3, 5}
B – A = {1, 2, 4, 6, 8, 10} – {1, 2, 3, 5, 8} = {4, 6, 10}
A ∩ B= {1, 2, 3, 5, 8} ∩ {1, 2, 4, 6, 8, 10} = {1, 2, 8}
A – B, B – A మరియు A ∩ B లలో ఉమ్మడి మూలకాలు లేవు.
కావున A – B, B – A, A ∩ Bలు వియుక్త సమితులు.

ఉదా : 2
A = {1, 2, 3, 4, 6, 8, 12, 24} B = {1, 2, 3, 6, 7, 14, 21, 42} అనుకుందాం.
వెన్ చిత్రాల ద్వారా A – B, B – A, A∩ B లను కనుగొందాము.

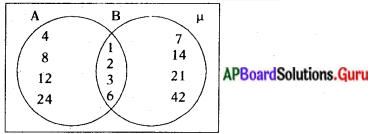
A – B = {4, 8, 12, 24}

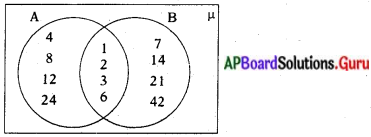
B – A {7, 14, 21, 42}

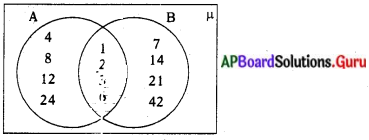
A ∩ B = {1, 2, 3, 6}
A- B, B – A, A ∩ Bలలో ఉమ్మడి మూలకాలు లేవు. కావున A – B, B – A, A ∩ B లు వియుక్త సమితులు.
గమనిక :
A – B, B – A, A ∩ Bలు పరస్పర వియుక్త సమితులు కాబట్టి
(A – B) ∩ (B – A ) = Φ
(B – A) ∩ (A ∩ B) = Φ
(A – B) ∩ (A ∩ B) = Φ.

ఇవి చేయండి:

ప్రశ్న 1.
క్రింది వానిలో శూన్యసమితులు ఏవి ? మీ సమాధానాన్ని సమర్థించండి.(పేజీ నెం. 44)
(i) 2 మరియు 3 ల మధ్యనున్న పూర్ణసంఖ్యల సమితి.
(ii) 1 కంటే తక్కువైన సహజసంఖ్యా సమితి.
(iii) 2 చే భాగించినపుడు శేషం సున్న వచ్చే బేసిసంఖ్యా సమితి.
సాధన.
(i) శూన్యసమితి.
2 మరియు 3ల మధ్య, పూర్ణసంఖ్యలు లేవు. కాబట్టి శూన్యసమితి అవుతుంది.
(ii) శూన్యసమితి.
సహజసంఖ్యలలో 1కన్నా తక్కువైన సహజసంఖ్య లేదు. కాబట్టి శూన్యసమితి.
(iii) శూన్యసమితి.
2చే భాగించినపుడు శేషం సున్న వచ్చే బేసి సంఖ్యలు లేవు. కాబట్టి శూన్యసమితి.

ప్రశ్న 2.
క్రింది సమితులలో ఏవి పరిమిత సమితులో, ఏవి అపరిమిత సమితులో తెలపండి. నీ సమాధానానికి తగిన కారణాలు ఇవ్వండి. (పేజీ నెం. 44)
(i) A = {x : x ∈ N మరియు x < 100}
(ii) B = {x : x ∈ N మరియు x < 5}
(iii) C = {1², 2², 3², …….}
(iv) D = {1, 2, 3, 4}
(v) {x : x వారంలో ఒక రోజు}
సాధన.
(i) A = {x: x ∈ N మరియు x < 100} పరిమిత సమితి.
A సమితిలో 1 నుండి 99 వరకు గల సహజ సంఖ్యలు ఉంటాయి. అనగా A పరిమిత సంఖ్యలో 99 మూలకాలను కలిగి ఉంది. కావున పరిమిత సమితి అవుతుంది
(లేదా)
A = {x : x ∈ N మరియు x < 100}
A = {1, 2, 3, 4, ….., 98, 99}
A సమితి 99 మూలకాలను కలిగి ఉంది, కావున A పరిమిత సమితి.

(ii) B = {x : x ∈ N మరియు x < 5} పరిమిత సమితి.
సమితి B లో 1, 2, 3, 4, 5 అనే మూలకాలు మాత్రమే ఉంటాయి. B సమితి పరిమిత సంఖ్యలో 5 మూలకాలను కలిగి ఉంది. కావున పరిమిత సమితి.
(లేదా)
B = {x : x ∈ N మరియు x ≤ 5}
∴ B = {1, 2, 3, 4, 5}
B సమితిలో పరిమిత సంఖ్యలో 5 మూలకాలు కలవు. కావున B పరిమిత సమితి

(iii) C = {1², 2², 3², ………..}
అపరిమిత సమితి.
C సమితిలోని మూలకాలైన వర్గ సంఖ్యలు అనంతముగా ఉన్నాయి. కావున C అపరిమిత సమితి.

(iv) D = {1, 2, 3, 4}
పరిమిత సమితి సమితి D లో నాలుగు మూలకాలు కలవు. కావున పరిమిత సమితి,

(v) E = {x : x వారంలో ఒక రోజు పరిమిత సమితి}
సమితి E లో 7 మూలకాలు ఉంటాయి. (వారానికి 7 రోజులు) కావున పరిమిత సమితి
(లేదా )

E = {x : x వారంలో ఒక రోజు}
E = {ఆదివారం, సోమవారం, మంగళవారం, బుధవారం, గురువారం, శుక్రవారం, శనివారం}
E లో 7 మూలకాలు కలవు. కావున పరిమిత సమితి.
సూచన : ఒక సమితి యొక్క కార్డినల్ సంఖ్యను మనం నిర్ణయించగలిగితే ఆ సమితి పరిమిత సమితి అవుతుంది.
పై సమస్యలో n(A) = 99
n(B) = 5
n(C) = నిర్ణయించలేము
n(D) = 4
n(E) = 7

ప్రశ్న 3.
క్రింది సమితులలో అపరిమిత సమితిని / చేయండి. (పేజీ నెం. 44)
(A) 10 కంటే తక్కువైన పూర్ణాంకాల సమితి
(B) 10 కంటే తక్కువైన ప్రధానసంఖ్యల సమితి
(C) 10 కంటే తక్కువైన పూర్ణసంఖ్యల సమితి
(D) 10 యొక్క కారణాంకాల సమితి
సాధన.
(A) x
(B) ×
(C) ✓
(D) X

ప్రయత్నించండి:

ప్రశ్న 1.
క్రింది సమితులలో ఏవి శూన్యసమితులు ? మీ సమాధానాన్ని సమర్థించండి. (పేజీ నెం. 44)
(i) A = {x : x² = 4 మరియు 3x = 9}.
(ii) ఒక తలంలోని మొత్తం త్రిభుజాలలో మూడు కోణాల మొత్తం 180° కంటే తక్కువైన త్రిభుజాల సమితి.
సాధన.
(i) A = {x : x² = 4 మరియు 3x = 9} శూన్యసమితి.
x² = 4 మరియు 3x = 9 అయ్యేటట్లు x విలువ వ్యవస్థితం కాదు. కావున Aలో ఎలాంటి మూలకాలు ఉండవు. కాబట్టి A శూన్యసమితి.
(ii) ఒక తలంలోని మొత్తం త్రిభుజాలలో మూడు కోణాల మొత్తం 180° కంటే తక్కువైన త్రిభుజాల సమితి శూన్యసమితి. ఏ త్రిభుజంలో అయినా మూడు కోణాల మొత్తం 180° కన్నా తక్కువగా ఉండవు. కాబట్టి శూన్యసమితి.

ప్రశ్న 2.
B = {x : x + 5 = 5} శూన్య సమితి కాదు. ఎందువలన ? (పేజీ నెం. 44)
సాధన.
x + 5 = 5 ⇒ x = 5 – 5
x = 0, B సమితిలో ‘0’ ఒక మూలకంగా కలదు కావున B శూన్యసమితి కాదు,
B = {0}

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
శూన్య సమితి పరిమిత సమితి అవుతుంది. ఈ వాక్యం సత్యమా ? లేదా అసత్యమా ? ఎందుకు? (పేజీ నెం. 44)
సాధన.
శూన్యసమితి పరిమిత సమితి. శూన్యసమితిలోని మూలకాల సంఖ్య సున్న (‘0’). సున్న ఒక పరిమిత సంఖ్య. కావున శూన్యసమితి పరిమిత సమితి.

(లేదా )

శూన్యసమితి పరిమిత సమితి కాదు అనుకొందాం. అప్పుడు శూన్యసమితి అపరిమిత సమితి అవుతుంది. అనగా శూన్యసమితిలో ‘అపరిమిత సంఖ్యలో మూలకాలుంటాయి. కాని ఇది శూన్యసమితిలో మూలకాలు ఉండవు అనడానికి విరుద్దము. కావున శూన్యసమితి పరిమిత సమితి కాదు అనుకోవడం విరోధాభాసం.
∴ శూన్యసమితి పరిమిత సమితి.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
n(A), n(B), n(A ∩ B) మరియు n(A ∪ R)ల మధ్య సంబంధం ఏమిటి ? (పేజీ నెం. 45)
సాధన.
n(A ∪ B) = n(A) + n(B) – n(A ∩ B) లేదా
n(A ∩ B) = n(A) + n(B) – n(A ∪ D) లేదా
n(A ∪ B) + n(A ∩ B) = n(A) + n(B)

ప్రశ్న 2.
సమితులు A మరియు B లు వియుక్త సమితులైతే n(AUD) ని. ఎలా కనుగొంటారు ? (పేజీ నెం. 45)
సాధన.
A మరియు B సమితులు వియుక్త సమితులైన ఆ రెండు సమితులకు ఉమ్మడిగా ఎటువంటి మూలకాలు ఉండవు.
అనగా n (A ∩ B) = 0
అపుడు n(A U B) = n(A) + n(B) – n(A ∩ B) నందు n(A ∩ B) = 0 ప్రతిక్షేపించగా n(A ∪ B) = n(A) + n(B) అగును.

ఉదాహరణలు:

ప్రశ్న 1.
నీ తరగతి విద్యార్థులలో మంగళవారం పాఠశాలకు హాజరుకాని వారిని సమితి A అని, బుధవారం హాజరుకాని విద్యార్థుల సమితి B అనుకొందాం. అపుడు A = {రోజా, రాము, రవి} మరియు B = {రాము , ప్రీతి, హనీఫ్ } ఇపుడు మనం మంగళవారం లేక బుధవారం పాఠశాలకు హాజరుకాని విద్యార్థుల సమితి K, అనుకుంటే అపుడు రోజా ∈ K అవుతుందా ? రాము ∈ K అవుతుందా ? రవి ∈ K అవుతుందా ? హనీఫ్ ∈ K అవుతుందా ? ప్రీతి ∈ K అవుతుందా ? అఖిల ∈ K అవుతుందా ? (పేజీ నెం. 35&36)
సాధన.
రోజా, రాము, రవి, హనీఫ్ మరియు ప్రీతి అందరూ K సమితికి చెందుతారు. కాని అఖిల K సమితికి చెందదు. అందువలన, K = {రోజా, రాము, రవి, హనీఫ్, ప్రీతి}
ఇక్కడ మనం K ని A, B సమితుల సమ్మేళనం అంటారు. A, B సమితుల సమ్మేళనమనగా . A మరియు B సమితులలోని ఉమ్మడి ‘మూలకాలను ఒకేసారి తీసుకొని రెండింటిలోని మూలకాలన్నింటిని కలిగి వున్న సమితి అని అర్థం, సమితుల సమ్మేళనంను ‘µ’ గుర్తుతో సూచిస్తాం.

సంకేతంగా A UB అని రాస్తూ A యూనియన్ B అని చదువుతాం.
A ∪ B = {x : x ∈ A లేదా x ∈ B}

ప్రశ్న 2.
A = {2, 5, 6, 8} మరియు B = {5, 7, 9, 1} అయిన A ∪ B కనుగొనుము. పేజీ నెం. 36)
సాధన.
A ∪ B = {1, 2, 5, 6, 7, 8, 9}.
A ∪ B రాసేటపుడు A,B సమితులలోని ఉమ్మడి మూలకమైన 5ని ఒకేసారి తీసుకొన్నామని గమనించవచ్చు.

ప్రశ్న 3.
A = {a, e, i, 0, u} మరియు B = {a, i, u} అయిన A ∪ B = A అని చూపండి. (పేజీ నెం. 36)
సాధన.
A ∪ B = {a, e, i, 0, u} = A అవుతుంది.
ఈ ఉదాహరణ ద్వారా సమితి A మరియు దాని ఉప సమితి B ల సమ్మేళనం సమితి A అవుతుందని తెలుస్తుంది.
అంటే B ⊂ A అయితే A ∪ B = A.

ప్రశ్న 4.
A = {1, 2, 3, 4} మరియు B = {2, 4, 6, 8} అయిన A ∪ Bని వెన్ చిత్రాలలో వివరించండి. (పేజీ నెం. 36)
సాధన.

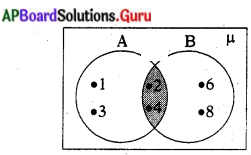
A ∪ B = {1, 2, 3, 4, 6, 8}

ప్రశ్న 5.
A = {5, 6, 7, 8} మరియు B = {7, 8, 9, 10} అయిన A ∩ B ని కనుగొనుము. (పేజీ నెం. 37)
సాధన.
A, B లలోని ఉమ్మడి మూలకాలు 7, 8.
∴ A ∩ B = {7, 8}.

ప్రశ్న 6.
A = {1, 2, 3} మరియు B = {3, 4, 5} అయిన A ∩ Bని వెన్ చిత్రాలలో వివరించండి. (పేజీ నెం. 37)
సాధన.
A, B సమితుల ఛేదనాన్ని వెన్ చిత్రాలలో క్రింది విధంలో చూపవచ్చు.

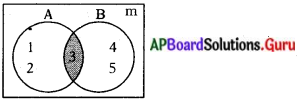
∴ A ∩ B = {3}.

ప్రశ్న 7.
A = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7} అనుకొనుము. A – Bని కనుగొనుము. (పేజీ నెం. 38)
సాధన.
A = {1, 2, 3, 4, 5} మరియు B = {4, 5, 6, 7} అని ఇవ్వబడినవి.
‘A’ సమితికి మాత్రమే చెంది, సమితి ‘B’ కి చెందని మూలకాలను మాత్రం తీసుకొనాలి.
A – B = {1, 2, 3, 4, 5} – {4, 5, 6, 7} = {1, 2, 3}.
∵ 4, 5 మూలకాలు B లో ఉన్నాయి.
కాబట్టి తీసుకోలేదు. అదేవిధంగా B – A అంటే, B సమితిలో ఉన్న మూలకాలను మాత్రమే తీసుకోవాలి.
B – A = {4, 5, 6, 7} – {1, 2, 3, 4, 5} .
B – A = {6, 7} (4, 5 మూలకాలు A లో ఉన్నాయి.)
A – B ≠ B – A అని గమనించండి.
A – B మరియు B – A ల వెన్ చిత్రం క్రింద చూపబడింది.

A – B = {1, 2, 3}
B – A = {6, 7}

ప్రశ్న 8.
క్రింది సమితులను తీసికుందాం. A = {p, q, r}, B = {q, p, r} (పేజీ నెం. 40)
సాధన.
పై సమితులలో A లోని ప్రతి మూలకం B లో కూడా ఉంది.
∴ A ⊆ B.
అదేవిధంగా సమితి B లోని ప్రతి మూలకం A లో కూడా ఉంది.
∴ B ⊆ A.

ప్రశ్న 9.
A = {1, 2, 3, ……} మరియు ‘N’ సహజ సంఖ్యా సమితి. అయిన A మరియు Nలు సమానమవుతాయేమో సరిచూడండి: (పేజీ నెం. 40)
సాధన.
రెండు సమితులలో మూలకాలు ఒకటి. కావున A మరియు N సమితులు రెండు కూడా సహజసంఖ్యా సమితులే. అందువలన సమితి A మరియు సమితి Nలు సమానం.
∴ A = N.

ప్రశ్న 10.
సమితులు A = {p, q, r, s} మరియు B= {1, 2, 3, 4} లు సమానమా ? (పేజీ నెం. 41)
సాధన.
సమితి A మరియు సమితి B లలో ఒకే మూలకాలు లేవు. కాబట్టి A ≠ B.

ప్రశ్న 11.
6 కంటే తక్కువైన ప్రధానాంకాల సమితిని A అనుకోండి. మరియు 30 కి ప్రధాన కారణాంకాలు గల సమితిని P అనుకోండి. A మరియు P సమానమా? సరిచూడండి. (పేజీ .నెం. 41)
సాధన.
6 కంటే తక్కువైన, ప్రధానాంకాల సమితి
A = {2, 3, 5}
30 కి ప్రధాన కారణాంకాలు 2, 3 మరియు 5. కావున
P= {2, 3, 5}
సమితి A మరియు Pలలో ఒకే రకమైన మూలకాలున్నాయి. కాబట్టి A మరియు P సమానం.

ప్రశ్న 12.
A = {x : x అనేది ‘ASSASSINATION అనే పదంలోని అక్షరం}
S = {x : x అనేది STATION అనే పదంలోని అక్షరం} అయిన A మరియు B సమితులు సమానం అని చూపండి. (పేజీ నెం. 41)
సాధన.
A = {x : x అనేది ‘ASSASSINATION’ అనే పదంలోని అక్షరం} అని ఇవ్వబడినది.
సమితి Aని ఈ విధంగా కూడా రాయవచ్చు.
A = {A,S, I, N,T,0}. ఎందుకంటే సమితిలోని మూలకాలు మరలా మరలా రాయకూడదు
B = {x : x అనేది STATION అనే పదంలోని అక్షరం} అని ఇవ్వబడింది.
B = {A, S,I, N,T,O} అని కూడా రా యవచ్చు కావున A మరియు B లోని మూలకాలు సమానం
A = B.

ప్రశ్న 13.
Φ, A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9} సమితులను తీసుకొందాం.. క్రింది ప్రతి సమితుల జతలలో C లేదా 4 గుర్తును ఉంచండి.
(i) Φ …… B
(ii) A …… B
(iii) A …… C
(iv) B …… C (పేజీ నెం: 41)
సాధన.
(i) Φ ⊂ B ఎందుకంటే శూన్య సమితి ప్రతి సమితికి ఉపసమితి అవుతుంది.
(ii) A ⊄ B, ఎందుకంటే 3 ∈ A కాని 3 ∉ B.
(iii) A ⊂ C, ఎందుకంటే 1, 3 ∈ A మరియు C.
(iv) B ⊂ C, ఎందుకనగా B లో ఉన్న ప్రతి మూలకం C లో కూడా ఉన్నది.

ప్రశ్న 14.
క్రింది సమితులలో ఏవి పరిమిత సమితులో, లేక అపరిమిత సమితులో పేర్కొనండి. (పేజీ నెం. 43)
(i) {x : x ∈ N మరియు (x – 1) (x – 2) = 0}
(ii) {x : x ∈ N మరియు x² = 4}
(iii) {x : x ∈ N మరియు 2x – 2 = 0}
(iv) {x : x ∈ N మరియు X ప్రధానసంఖ్య}
(v) {x : x ∈ N మరియు X బేసిసంఖ్య }
సాధన.
(i) ఈ సందర్భంలో X కి 1 లేదా 2 విలువలను – తీసుకోవచ్చు. కావున {1, 2} పరిమిత సమితి అవుతుంది. ఇది పరిమిత సమితి.
(ii) x² = 4 అనగా x = + 2 లేక – 2 కాని x ∈ N లేదా x ఒక సహజ సంఖ్య కాబట్టి {2}గా తీసుకోవాలి. ఇది కూడా పరిమిత సమితే,
(iii) దత్తసమితి x = 1 కాని 1 ∈ N కావున ఇది కూడా పరిమిత సమితి.
(iv) దత్తసమితిలో అన్నీ ప్రధాన సంఖ్యలు ఉన్నాయి. ప్రధానసంఖ్యలు అనంతము కావున ఈ సమితి అపరిమిత సమితి.
(v) దత్తసమితిలో అనంతమైన బేసి సంఖ్యలున్నాయి. కావున ఈ సమితి కూడా అపరిమిత సమితియే.

ప్రశ్న 15.
A = {1, 2, 3, 4, 5}; B = {2, 4, 6, 8}; అయిన n(A ∪ B) కనుగొనండి. (పేజీ నెం. 45)
సాధన.
A = {1, 2, 3, 4, 5,} ⇒ n(A) = 5
B = {2, 4, 6, 8} ⇒ n(B) = 4
A ∪ B = {1, 2, 3, 4, 5, 6, 8} ⇒ n(AU B) = 7