AP Board 10th Class Maths Solutions Chapter 14 సాంఖ్యకశాస్త్రం Exercise 14.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 14 సాంఖ్యకశాస్త్రం Exercise 14.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 14th Lesson సాంఖ్యకశాస్త్రం Exercise 14.1

ప్రశ్న 1.
ఒక గ్రామంలో కొంతమంది విద్యార్థుల జట్టు ‘పర్యావరణ పరిరక్షణ – అవగాహన’ అనే కార్యక్రమంలో భాగంగా, 20 – ఇండ్లలో సర్వే నిర్వహించి, ఎన్నెన్ని మొక్కలు నాటినారో సమాచారాన్ని సేకరించి, ఈ క్రింది పట్టికలో నమోదు చేసినారు. సగటున ఒక ఇంటికి ఎన్ని మొక్కలు నాటినారో కనుక్కోండి.

సాధన.

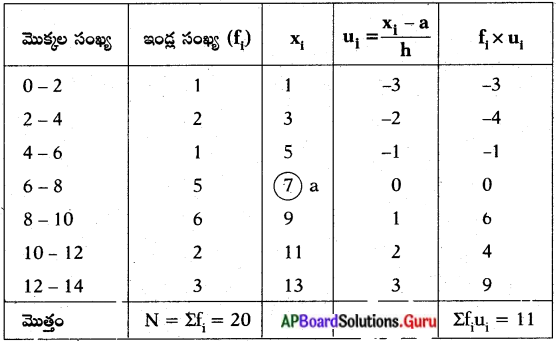
దత్తాంశం యొక్క సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
a = ఊహించిన సగటు = 7
Σf_iu_i = 11
Σf_i = 20
h = 2
సగటు చెట్ల సంఖ్య (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 7 + \(\frac{11}{20}\) × 2
= 7 + 1.1
∴ సగటు చెట్ల సంఖ్య (\(\overline{\mathbf{x}}\)) = 8.1

ప్రశ్న 2.
ఒక కర్మాగారంలోని 50 మంది కార్మికుల దినసరి భత్యము ఈ క్రింది పౌనఃపున్య విభాజన పట్టికలో ఇవ్వబడినవి.

తగు పద్ధతిని ఎంచుకొని ఆ కర్మాగారంలోని కార్మికుల సగటు భత్యమును కనుక్కోండి.
సాధన.

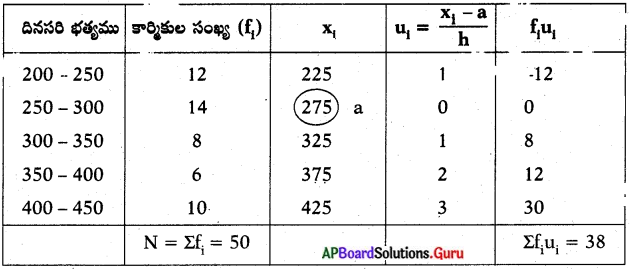
దత్తాంశం యొక్క సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
a = ఊహించిన సగటు = 275
Σf_iu_i = 38
Σf_i = 50
h = 50
∴ కార్మికుల సగటు భత్యము (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 275 + \(\frac{38}{50}\) × 50 = 275 + 38
∴ కార్మికుల సగటు భత్యము (?) = 313.

ప్రశ్న 3.
ఒక ఆవాసప్రాంతంలో పిల్లల రోజువారి చేతి ఖర్చులు (pocket allowance) వివరాలను ఈ క్రింది పౌనఃపున్య విభాజన పట్టికలో ఇవ్వడమైనది. పిల్లల సగటు చేతి ఖర్చు ( 18 అయిన క్రింది పట్టికలో లోపించిన పౌనఃపున్యం(f)ను కనుగొనుము.

సాధన.

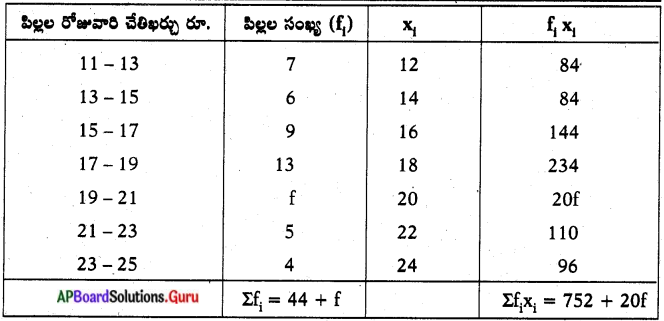
దత్తాంశం యొక్క సగటు \(\overline{\mathbf{x}}\) = 18
పౌనఃపున్యం యొక్క విలువ (f) = ?
∴ Σf = 44 +f
Σf_iu_i = 752 + 20f
∴ సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
⇒ \(\frac{752+20 \mathrm{f}}{44+\mathrm{f}}\) = 18
⇒ 752 + 20f = 792 + 18f
⇒ 2f = 40
∴ లోపించిన పౌనఃపున్యం (f) = 20.

ప్రశ్న 4.
ఒక వైద్యశాలలో వైద్యులు 30 మంది స్త్రీలకు వైద్య పరీక్షలు నిర్వహించి, వారి యొక్క హృదయ స్పందనలను క్రింద చూపిన పట్టికలో క్రోడీకరించారు. తగు విధానాన్ని ఎంచుకొని ఇట్టి స్త్రీల యొక్క హృదయస్పందనల సరాసరి (ఒక నిమిషానికి). కనుక్కోండి.

సాధన.

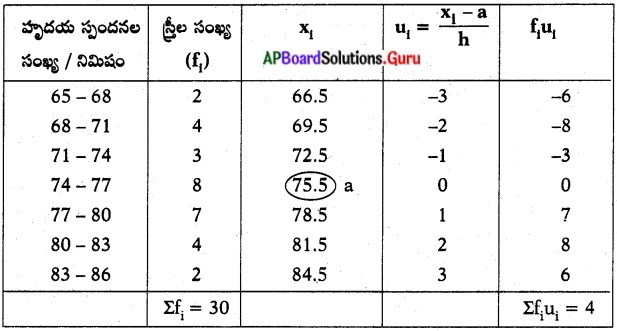
∴ తరగతి అంతరం (h) = 3
Σf_ix_i = 4
Σf_i = 30
ఊహించిన సగటు (a) = 75.5
∴ హృదయ స్పందనల సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 75.5 + \(\frac{4}{30}\) × 3
= 75.5 + 0.4 = 75.9
∴ హృదయ స్పందనల సగటు (\(\overline{\mathbf{x}}\)) = 75.9.

ప్రశ్న 5.
పండ్ల మార్కెట్లో, పండ్ల వ్యాపారులు ‘నారింజపండ్లను పెట్టెలలో ఉంచి అమ్ముతారు. ఒక్కొక్క పెట్టెలో ఉండే ‘నారింజపండ్ల’ సంఖ్య వేరువేరుగా ఉంటుంది. పెట్టెల్లోని నారింజపండ్ల పంపకాన్ని ఈ క్రింది

ఒక్కొక్క పెట్టెలో ఉండే నారింజపండ్ల సగటు కనుక్కోండి. సగటు కనుగొనుటకు ఏ పద్ధతిని ఎంచుకుంటారో తెల్పండి.
సాధన.

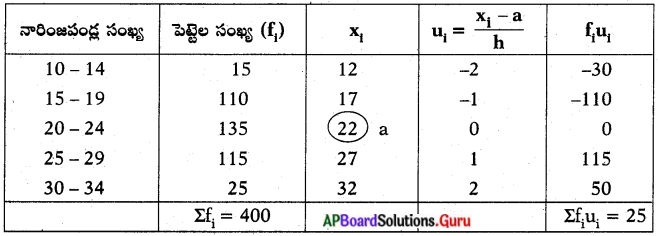
∴ ఊహించిన సగటు (a) = 22
Σf_i = 400
Σf_iu_i = 25
h = 5
సగటును కనుగొనుటకు సంక్షిప్త విచలన పద్ధతిని ఎంచుకొంటాం.
∴ సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 22 + \(\frac{25}{400}\) × 5
= 22 + 0.31 = 22.31
∴ ఒక్కొక్క పెట్టెలోని నారింజపండ్ల సగటు సంఖ్య (\(\overline{\mathbf{x}}\)) = 22.31.

ప్రశ్న 6.
ఒక ఆవాసప్రాంతంలోని 25 కుటుంబాలకు సంబంధించిన దినసరి భోజన ఖర్చుల వివరాలను ఈ క్రింది పట్టికలో ఇవ్వడమైనది.

తగు పద్ధతిని ఎంచుకొని, ఒక్కో కుటుంబానికి అయ్యే సగటు భోజన ఖర్చును కనుక్కోండి.
సాధన.

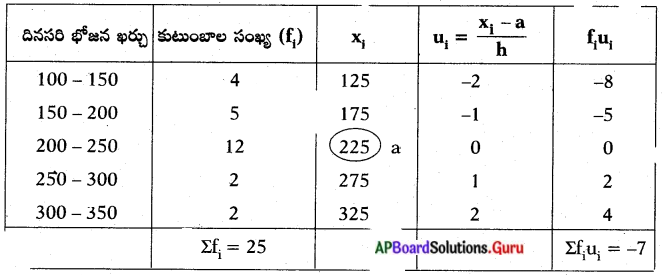
ఊహించిన సగటు (a) = 225
Σf_iu_i = – 7
Σf_i = 25
తరగతి యొక్క అంతరం (h) = 50
ఒక్కో కుటుంబానికి అయ్యే సగటు భోజన ఖర్చు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 225 + \(\frac{(-7)}{25}\) × 50
= 225 – 14
LI . ఒక్కో కుటుంబానికి అయ్యే సగటు భోజన ఖర్చు (\(\overline{\mathbf{x}}\)) = 211.

ప్రశ్న 7.
ఒక పట్టణంలోని 30 నివాస ప్రాంతాలలో, గాలిలో గల’ SO₂ యొక్క గాఢత (in parts per million, i.e., ppm) ను ఈ క్రింది పట్టికలో క్రోడీకరించడమైనది.

గాలిలో గల సగటు SO₂ గాఢతను కనుక్కోండి
సాధన.

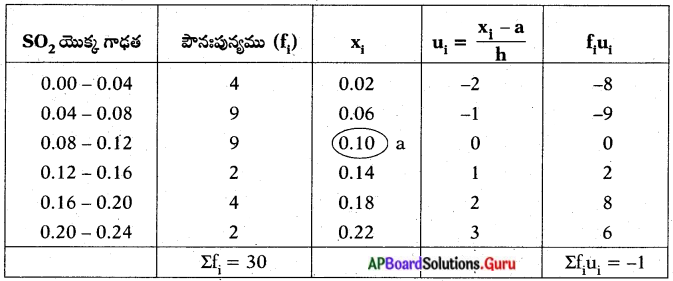
ఊహించిన సగటు (a) = 0.1
Σf_iu_i = – 1
Σf_i = 30, h = 0.04
∴ గాలిలో గల SO₂ గాఢత సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 0.1 – \(\frac{(-1)}{30}\) × 0.04
= 0.1 – 0.00133
= 0.09867 ppm
∴ గాలిలో గల SO₂ గాఢత సగటు (\(\overline{\mathbf{x}}\)) = 0.099 ppm.

ప్రశ్న 8.
ఒక తరగతి ఉపాధ్యాయుడు ఒక టర్న్ లో తన తరగతికి చెందిన 40 మంది విద్యార్థుల హాజరు వివరాలను, ఈ క్రింది చూపిన పట్టికలో చూపడమైనది. ఈ టర్న్ లో ఒక విద్యార్థి సగటు హాజరు ఎంత ?

సాధన.

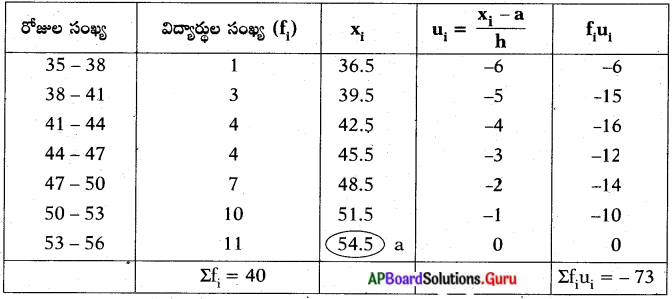
ఊహించిన సగటు (a) = 54.5
Σf_iu_i = 73 .
Σf_i = 40
h = 3
సగటు = (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 54.5 + \(\frac{(-73)}{40}\) × 3
= 49.025 = 49 రోజులు
టర్న్ లో ఒక విద్యార్థి సగటు హాజరు (\(\overline{\mathbf{x}}\)) = 49 రోజులు.

ప్రశ్న 9.
35 పట్టణాలకు సంబంధించి అక్షరాస్యత రేటు (శాతములలో) ఈ క్రింది పట్టికలో ఇవ్వడమైనది. సగటు అక్షరాస్యత రేటును కనుక్కోండి.

సాధన.

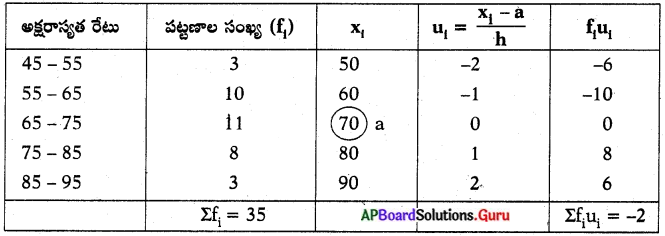
∴ ఊహించిన సగటు (a) = 70
Σf_i = 35
Σf_iu_i = – 2
h = 10
∴ సగటు (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 70 + \(\frac{(-2)}{35}\) × 10
= 70 – \(\frac{20}{35}\) = 70 – 0.57
సగటు అక్షరాస్యత రేటు (\(\overline{\mathbf{x}}\)) = 69.43 %