AP Board 10th Class Maths Solutions Chapter 10 క్షేత్రమితి Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Optional Exercise

ప్రశ్న 1.
4.1 సెం.మీ. వ్యాసము కల్గిన ఒక గోల్ఫ్ బంతి ఉపరితలముపై 2 మి.మీ వ్యాసార్ధం కలిగిన 150 బొడిపెలు (డింపుల్స్) ఉన్నవి. డింపుల్స్ అర్ధ గోళాకారంలో ఉన్నవి అని భావిస్తే వాటి మొత్తము ఉపరితల వైశాల్యము ఎంత? [π = \(\frac{22}{7}\)]
సాధన.
మొత్తం బొడిపెల వైశాల్యం = బంతి యొక్క ఉపరితల వైశాల్యము – 2 మి.మీల – వ్యాసార్ధం గల 150 వృత్తాల వైశాల్యం
= 4πr₁² – 150 x πr₂²
= 4 × \(\frac{22}{7} \times \frac{4.1}{2} \times \frac{4.1}{2}\) – 150 × \(\frac{22}{7} \times \frac{2}{10} \times \frac{2}{10}\)
(∵ గోల్ఫ్ బంతి యొక్క వ్యాసార్థం (r) = \(\frac{\mathrm{d}}{2}\)
= \(\frac{4.1}{2}\) సెం.మీ.
బుడిపె ఒకొక్క వ్యాసార్థం (r) = \(\frac{\mathrm{d}}{2}\) = 2 మి.మీ.
= \(\frac{2}{10}\) సెం.మీ.)
= 58.831 – 18.57 = 40.261 సెం.మీ².

ప్రశ్న 2.
12 సెం.మీ. వ్యాసార్ధము కల్గిన ఒక స్థూపాకార పాత్రలో 20 సెం.మీ. లోతు మేరకు నీరు నింపబడియున్నది. ఒక ఇనుప గోళమును దానిలో విడిస్తే నీటి మట్టము 6.75 సెం.మీ. పెరిగినది. అయినచో విడువబడిన గోళము యొక్క వ్యాసార్ధము ఎంత ? [π = \(\frac{22}{7}\)]
సాధన.
స్థూపాకార పాత్ర వ్యాసార్ధం (r) = 12 సెం.మీ.
ఎత్తు (h) = 6.75 సెం.మీ.
పెరిగిన నీటి మట్టం యొక్క ఘనపరిమాణం = నీటిలో జారవిడిచిన గోళాల(సంఖ్య) ఘనపరిమాణం
⇒ πr₁²h = \(\frac{4}{3}\) πr₂³
⇒ r₁²h = \(\frac{4}{3}\) r₂³
⇒ 12 × 12 × 6.75 = \(\frac{4}{3}\) × r₂³
r₂³ = \(\frac{3}{4}\) × 12 × 12 × 6.75 = 9 × 12 × 6.75
⇒ r₂³ = 729 = 9³
∴ r₂ = 9 సెం.మీ.
∴ ఒక్కొక్క గోళం వ్యాసార్ధం = 9 సెం.మీ.

ప్రశ్న 3.
ఒక ఘనపు ఆట వస్తువు స్థూపాకృతిలో ఉండి ఒక చివర అర్ధగోళాకారాన్ని మరో చివర శంఖువు ఆకారాన్ని కలిగి ఉంది. వాటి ఉమ్మడి వ్యాసము 4.2 సెం.మీ. స్థూపాకార భాగము, శంఖువాకార భాగముల ఎత్తులు వరుసగా 12 సెం.మీ. మరియు 7 సెం.మీ. అనుకొంటే ఆ ఘనపు ఆటవస్తువు యొక్క ఘనపరిమాణము ఎంత ? [π = \(\frac{22}{7}\)]
సాధన.

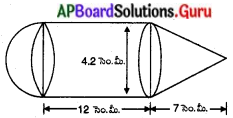
ఆట వస్తువు యొక్క ఘనపరిమాణం = అర్ధగోళ ఘనపరిమాణం + స్థూపం ఘనపరిమాణం + శంఖువు ఆకార ఘనపరిమాణం
= \(\frac{2}{3}\) πr³ + πr²h₁ + \(\frac{1}{3}\) πr²h₂
= πr² (\(\frac{2}{3}\) + h₁ + \(\frac{\mathrm{h}_{2}}{3}\))
= \(\frac{22}{7} \times \frac{4.2}{2} \times \frac{4.2}{2}\left[\frac{2}{3} \times \frac{4.2}{2}+12+\frac{7}{3}\right]\)
[∵ r = \(\frac{\mathrm{d}}{2}=\frac{4.2}{2}\)]
[∵ h = 12 సెం.మీ]
= 11 × 0.6 × 2.1 [1.4 + 12 + \(\frac{7}{3}\)]
= 13.86 [13.4 + 3]
= 13.86 × \(\frac{47.2}{3}\) = 218.064 సెం.మీ³.

ప్రశ్న 4.
15 సెం.మీ., 12 సెం.మీ. మరియు 9 సెం.మీ. భుజములుగా గల మూడు లోహపు ఘనములను కరిగించి ఒక ఘనముగా మారిస్తే, ఏర్పడిన ఘనము యొక్క కర్ణము పొడవు ఎంత ?
సాధన.

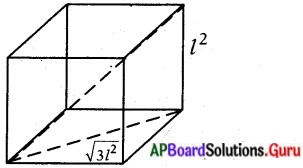
మూడు లోహ సమఘనాల భుజాలు వరుసగా l₁ = 15 సెం.మీ.; l₂ = 12 సెం.మీ. l₃ = 9 సెం.మీ.
పై మూడు సమఘనాలను కరిగించిన ఒక పెద్ద సమఘనం తయారు చేయగా దాని ఘనపరిమాణం
l³ = l₁³ + l₂³ + l₃³
= 15³ + 12³ + 9³
= 3375 + 1728 + 729
= 5832 = 18 x 18 x 18
⇒ l³ = 18³
⇒ l = 18 సెం.మీ.
∴ నూతన సమఘనం యొక్క కర్ణం పొడవు = √3l = √3 × 18
= 1.732 × 18 = 31.176 సెం.మీ.

ప్రశ్న 5.
36 సెం.మీ. అంతర వ్యాసార్థం కల్గిన ఒక అర్ధ గోళాకార పాత్ర ద్రవముతో నింపబడి యున్నది. ఆ ద్రవమును 3 సెం.మీ. వ్యాసార్ధము మరియు 6 సెం.మీ. ఎత్తు కల్గిన స్థూపాకార సీసాలలో నింపితే, మొత్తం ద్రవముగా నింపడానికి అవసరమయ్యే సీసాల సంఖ్య ఎంత ?
సాధన.

అర్ధగోళాకార పాత్ర యొక్క వ్యాసార్ధం = r₁ = 36 సెం.మీ.
అర్ధగోళాకార పాత్రలో నింపబడిన ద్రవం ఘ॥ప = \(\frac{2}{3}\) πr₁³
n సీసాలలో నింపబడే ద్రవం ఘ||ప = (n) πr₂²h
ఇక్కడ r₂ అనగా స్థూపాకార సీసా వ్యాసార్ధం = 3 సెం.మీ.
h అనగా స్తూపాకార సీసా వ్యాసార్ధం = 6 సెం.మీ.
∴ అర్ధగోళాకార పాత్ర ఘ॥ప = n సీసాలలోని ద్రవం ఘ॥
\(\frac{2}{3}\) πr₁³ = (n) πr₂²h
విలువలు ప్రతిక్షేపించగా
\(\frac{2}{3}\) × \(\frac{22}{7}\) × 36 × 36 × 36 = n × \(\frac{22}{7}\) × 3 × 3 × 6
∴ n = \(\frac{2 \times 12 \times 22 \times 36 \times 6}{22 \times 9}\) = 576
అనగా 576 సీసాలు అవసరమగును.