These AP 9th Class Maths Important Questions 6th Lesson Linear Equation in Two Variables will help students prepare well for the exams.
AP State Syllabus 9th Class Maths 6th Lesson Important Questions and Answers Linear Equation in Two Variables
Question 1.
Express the following statement as a linear equation in two variables. “Neeraja and Girija of class IX students together contributed Rs. 300/- towards the C.M. relief fund”.
Solution:
Contribution of Neeraja = ₹x
Contribution of Girija = ₹y
Sum of contribution of Neeraja and Girija is 300/-
∴ x + y = 300.
Question 2.
Re state the following statement with appropriate conditions to make it true statement.
“For every real number x, x2 ≥ x”.
Solution:
If x ≤ 0 or x ≥ 1 then x2 ≥ x.
For every integer x, x2 ≥ x.
Question 3.
Write the statement given below as a linear equation two in variables. “The sum of two numbers x and y is 75”.
Solution:
The sum of two numbers x and y is 75.
∴ x + y = 75
![]()
Question 4.
If x = 2 – α and y = 2 + α in a solution of 5x + 3y – 7 = 0 and x = 2β + 1 and y = β – 1 in a solution of 3x – 2y + 6 = 0 then find the value of α + β.
Solution:
Given equation = 5x + 3y – 7 = 0
x = 2 – α and y = 2 + α
∴ 5(2 – α) + 3(2 + α) – 7 = 0
⇒ 10 – 5α+ 6 + 3α – 7 = 0
⇒ 9 – 2α = 0
⇒ 2α = 9 ⇒ α = \(\frac{9}{2}\) = 4.5
Given equation 3x – 2y + 6 = 0
x = 2β + 1 and y = β – 1
∴ 3(2β + 1)- 2(β – 1) + 6 = 0
⇒ 6β + 3 – 2β + 2 + 6 = 0
⇒ 4β + 11 = 0 ⇒ β = \(\frac{-11}{4}\)
∴ α + β = \(\frac{9}{2}\) – \(\frac{11}{4}\) = \(\frac{18-11}{4}\) = \(\frac{7}{4}\)
Question 5.
Draw the graph of the equation 2x + 3y = 6. Find the coordinates of the points where the graph cuts the coordinate axes.
Solution:
Given equation 2x + 3y = 6

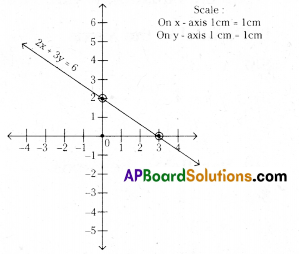
Coordinates of the points are (3, 0) (0, 2)
Question 6.
Draw the graph of the linear equations 2x + 3y = 12. At what points, the graph of the equation cuts the X-axis and Y-axis.
Solution:
2x + 3y = 12

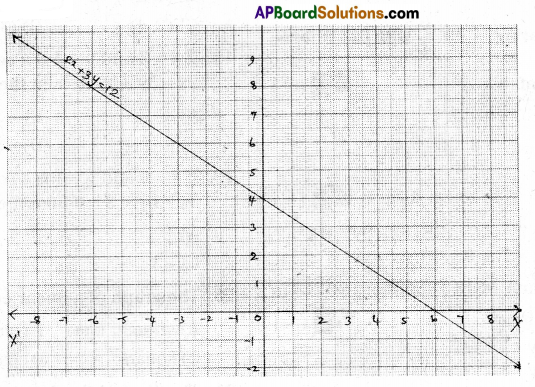
The graph of the equation cuts the x – axis = (6, 0)
y – axis = (0, 4)
