AP 9th Class Maths Important Questions Chapter 5 Co-Ordinate Geometry

These AP 9th Class Maths Important Questions 5th Lesson Co-Ordinate Geometry will help students prepare well for the exams.

AP State Syllabus 9th Class Maths 5th Lesson Important Questions and Answers Co-Ordinate Geometry

Question 1.
Write any point lies on \(\overline{\text { OY }}\) (Positive Y – axis) and any point lies on \(\overline{\text { OX }}\) (Negative X-axis).
Solution:
Point lies on \(\overline{\text { OY }}\) be (x = 0, y ≥ 0)
example : (0, 2) (0, 3).
Point lies on \(\overline{\text { OX }}\) be (x = 0, y ≤ 0)
example : (2, 0) (3, 0).

Question 2.
The position of (3, 4) and (4, 3) are not the same on graph. Why?
Solution:
Given points (3, 4) and (4, 3) having x and y coordinates are equal.

Question 3.
The points such as (0, x), (0, -x), (0, y) and (0, -y) lie on the same line. Name the line.
Solution:
That line is Y – axis.

Question 4.
The co-ordinates of a point M(4, – 3). What are the distances of the point M from axes?
Solution:
Given point = M(4, -3)
Distance from x -axis to the M is | -3 | units = 3
Distance from y – axis to the M is | 4 | units = 4

Question 5.
From the figure given below, write the co-ordinates of the points A, B, P and Q.

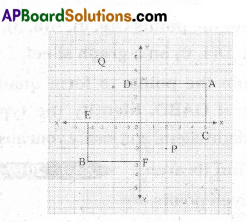
Solution:
A(5,3), B(-4, -3), P(2, -2), Q(-3, 4)

Question 6.
What is a cartesian plane? Explain with a diagram.
Solution:
1) To locate the exact position of a point on a number line we need only a single reference.
2) To describe the exact position of a point on a Cartesian plane we need two references.
3) The two perpendicular lines taken in any direction are referred to as co-ordinate axes.
4) The horizontal line is called X – axis.
5) The vertical line is called Y – axis.
6) The meeting point of the axes is called the origin.
7) The distance of a point from Y – axis is called the x co-ordinate or abscissa.
8) The distance of a point from X-axis is called the y co-ordinate or ordinate.
9) The co-ordinates of origin are (0, 0),
10 ) The co-ordinate plane is divided into four quadrants namely Q₁; Q₂, Q₃, Q₄ i.e., first, second, third and fourth quadrants respectively.
11) The signs of co-ordinates of a point are as follows.
Q₁(+, +); Q₂; (-, +)
Q₃(-, -); Q₄; (+, -)

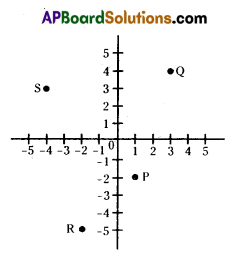
The coordinates of P are (1, – 2).
The coordinates of Q are (3, 4).
The coordinates of R are (- 2, – 5).
The co-ordinates of S are (- 4, 3).

Question 7.
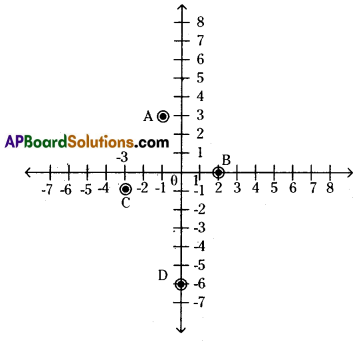
Without using graph sheet write the location of points given below.
(-1, 3), (2, 0), (-3, -1), (0, -6)
Solution:
Given points A(-1, 3), B(2, 0), C(-3, -1) and D(0, -6)

Question 8.
Plot the points A (2, 2) B (6, 2) C (8, 5) and D (4, 5) in a graph sheet. Join all the points to make it a parallelogram. Find its area.
Solution:

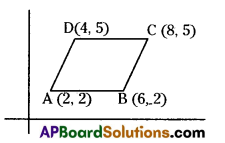
Area of parallelogram = AB × BC
AB = | x₂ – x₁ | = | 6 – 2 | = 4
BC = | y₂ – y₁ | = | 5 – 2 | = 3
∴ Area = 4 × 3 = 12 sq. units.

Question 9.
Read the following table and answer the following questions given below.

i) The point belongs to Q₃
ii) The abscissa of the point C
iii) The point lie on X – axis
iv) The coordinates of origin
v) The point satisfy x > 0, y < 0
vi) The point satisfy x – y = 1
vii) The position of point B
viii) The Quadrant contain (3,-2)
Solution:
i) D
ii) 3
iii) F, H
iv) 0,0
v) C (3, – 2)
vi) A (2, 1)
Vii) Positive Y-axis
viii) Q₄

Question 10.
i) Plot the points 0(0, 0), A(0, 3), B(4, 3), D(4, 0) on a graph sheet.
ii) Join the points to form quadrilateral OABD. Identify the type of quadrilateral and Justify your answer.
iii) Find its area.
Solution:
i) Given points are
O(0, 0), A(0, 3), B(4, 3), D(4, 0)

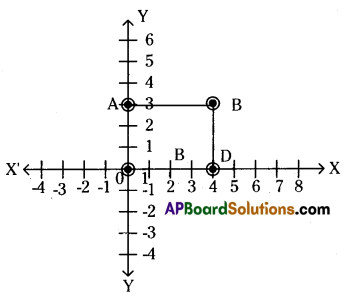
ii) OABD represents a rectangle.
iii) Area of a rectangle OABD
= l × b = OD × BD = 4 × 3 = 12 sq units.

Question 11.
i) Plot the points A(2, 3), B(6, 3), C(4, 7) on a graph sheet.
ii) Join the points to form triangle ABC. Identify the type of triangle and justify your answer.
iii) Find its area,
Solution:
i) given points are A(2, 3), B(6, 3), C(4, 7)

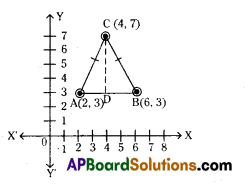
ii) ΔABC is formed, which is an Isosceles triangle.
CD = | 7 – 3 |= 4 units
AB = |16 – 2 | =4 units

iii) Area of ΔABC = \(\frac{1}{2}\) × b × h .
= \(\frac{1}{2}\) × AB × CD
= \(\frac{1}{2}\) × 4 × 4
= 2 × 4 = 8 sq units