These AP 9th Class Maths Important Questions 4th Lesson Lines and Angles will help students prepare well for the exams.
AP State Syllabus 9th Class Maths 4th Lesson Important Questions and Answers Lines and Angles
Question 1.
∠POR and ∠QOR is a linear pair. If ∠POR = 3x° and ∠QOR = (2x + 10)° then find the value of x.
Solution:
∠POR and ∠QOR is a linear pair.
So ∠POR + ∠QOR = 180°
3x + 2x + 10° = 180°
5x + 10° = 180°
5x = 180 – 10
5x = 170°
x = \(\frac{170}{5}\) = 34°
∴ x = 34°.
Question 2.
Draw an equilateral triangle whose sides are 6 cm each.
Solution:
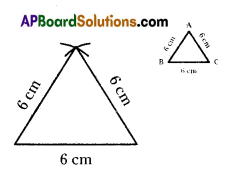
![]()
Question 3.
Write all pairs of vertically opposite angles from the diagram.

Solution:
From figure Vertically opposite angles are respectively
∠AOB = ∠COD and ∠AOD = ∠BOC
Question 4.
An exterior angle of a triangle is 110° and one of the interior opposite angle is 30°. Find the other two angles of the triangle.
Solution:
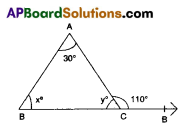
∠A = 30°, ∠ACD = 110°, ∠B = x, ∠C = y 30 + x = 110°
(By exterior angle property)
x = 80°
y + 110° = 180° (∵ linear pair)
y = 70°
∴ Remaining angles are x = 80° and y = 70°.
Question 5.
Find the value of ‘x’ in the figure.
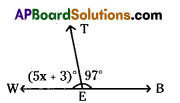
From Figure
(5x + 3)° + 97° = 180° {∵ Linear pair}
5x + 100° = 180°
5x = 180° – 100° ⇒ 5x = 80°
x = \(\frac{80}{5}\) = 16°
∴ x = 16°.
Question 6.
If ∠1 + ∠2 < 180° what can you say about lines l and m?
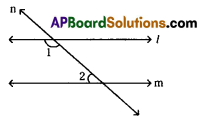
Solution:
∠1 & ∠2 are two interior angles that lie on same side of transversal ‘n’.
As their sum is less than 180°, the two lines intersect at that side.
∴ The two lines ‘l’ and ‘m’ are two intersecting lines at the side of the angles ∠1 & ∠2.
Question 7.
In the following figure \(\overline{\mathbf{A B}}\) is a straight line. OP and OQ are two rays. Find the value of x and also find ∠AOP and ∠AOQ.
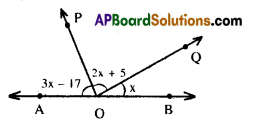
Solution:
\(\overline{\mathbf{A B}}\) is a straight line
Sum of the angles formed at ‘O’ is 180°
∴ 3x – 17 + 2x + 5 + x = 180°
6x – 12 = 180°
6x = 192° ⇒ x = 32°
∴ ∠AOP = 3x -17 = 96 – 17 = 79°
∠POQ = 2x + 5 = 64 + 5 = 69°
∠AOQ = 79° + 69 = 148°.
![]()
Question 8.
l // m and ‘n’ is transversal.
If ∠b = (3x – 10)° and ∠h = (5x – 30)° then determine all the angles.
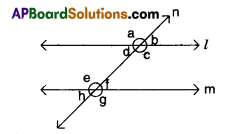
Solution:
In figure l // m, so ∠b = ∠h
3x – 10 = 5x – 30
-2x = -20 ⇒ x = 10°
∠b = 3x – 10 = 3 × 10 – 10 = 20°
∠a = 180 – ∠b = 180 – 20 = 160°
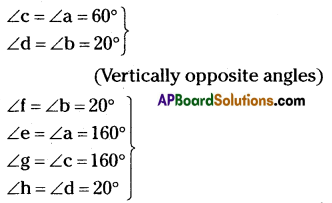
(corresponding angles)
∴ ∠b = ∠d = ∠f = ∠h = 20°
∠a = ∠c = ∠e = ∠g = 160°.
Question 9.
In the given figure, the lines, p, q and r are parallel to one another. Find the values of a, b, c, x, y and z.
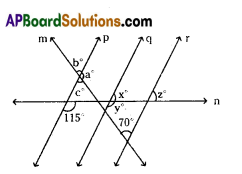
Solution:
From given figure .
y = 115° {∵ Corresponding angles}
⇒ x + y = 180° {linear pair}
⇒ x = 180°- y = 180° – 115° = 65°
⇒ z = x°= 65° { ∵ Corresponding angles}
c° – 70°
a° + c° = 180° {linear pair}
⇒ a° + 70° = 180°
⇒ a° = 180° – 70° = 110°
b° = c° = 70°
{Vertically opposite angles}
So, a = 110°, b = 70°, c = 70°, x = 65°,
y = 115°, z = 65°
Question 10.
Calculate the values of ‘x’ and ‘y’ using the information given in the figure.
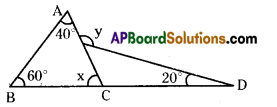
Solution:
From ΔABC
∠A + ∠B + ∠C = 180°
⇒ 40° + 60° + x° = 180°
⇒ x = 180° – 100° ⇒ x = 80°.
∠DCA = 180° – ∠x
[ ∵ ∠BCA, ∠DCA forms a linear pair]
∠DCA = 180° – 80° = 100°
∴ ∠y = ∠DCA + 20°[ ∵ exterior angle of ’ a triangle is equal to the = 100° + 20°
sum of its two opposite interior angles
∠y = 120°.
Question 11.
In the adjacent figure AB // CD. Find ‘ the values of x, y and z.
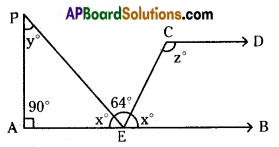
Solution:
Given that AB//CD
From the adj. fig. ∠AEP + ∠PED + ∠BEC
= 180° (∵ straight angle)
⇒ x° + 64° + x° = 180°
⇒ 2x = 180° – 64° = 116°
x = \(\frac{116^{\circ}}{2}\) = 58°
Now ∠z + ∠x = 180° [ ∵ AB//CD Zx, Zz are interior angles which are formed same side of the transversal line]
⇒∠z + 58° = 180° ⇒ ∠z = 180° – 58°
∴ ∠z = 122°.
from ΔAPE
∠A + ∠P + ∠E = 180°
⇒ 90° + ∠y + ∠x = 180°
⇒ 90° + ∠y + 58° = 180°
⇒ ∠y = 180° – 148° ⇒ ∠y = 32°
⇒ ∠x = 58°, ∠y = 32°, ∠z = 122°.
![]()
Question 12.
In the given figure \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\). Find the values of x and y.
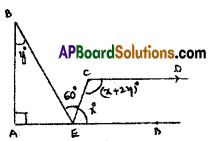
Solution:
Given that AB // CD.
From the figure x° + 60° + x° = 180°
( ∵ The angles at a point on the line)
2x = 180° – 60° ⇒ x = \(\frac{120^{\circ}}{2}\) = 60°
We know x° + x° + 2y° = 180°
[∵ interior angles on the same side of transversal]
2x°+ 2y° = 180°
2y° = 180° – 2x°
2y° = 180° – 2 (60°) = 60°
y = 30°
