AP 9th Class Maths Important Questions Chapter 2 Polynomials and Factorisation

These AP 9th Class Maths Important Questions 2nd Lesson Polynomials and Factorisation will help students prepare well for the exams.

AP State Syllabus 9th Class Maths 2nd Lesson Important Questions and Answers Polynomials and Factorisation

Question 1.
Find the value of p (\(\frac{2}{3}\)) for p(y) = 2y³ – y² – 13y – 6.
Solution:
Given polynomial
p(x) = 2y³ – y² – 13y – 6

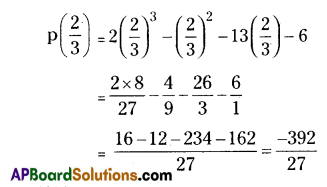
Question 2.
If ‘2’ is a zero of the polynomial P(x) = 4x² – 3x + 5a then find the value of a.
Solution:
Given polynomial P(x) = 4x² – 3x + 5a
the zero of the polynomial is ‘2’, we know that p(2) = 0
P(x) = 0.
4(2)² – 3(2) + 5a = 0
16 – 6 + 5a = 0
5a = -10
a = \(\frac{-10}{5}\) = -2
a = -2.

Question 3.
Applying a suitable identity find the product of (x – y), (x + y) and (x² + y²).
Solution:
(x + y) (x – y) (x² + y²) = (x² – y²)
(x² + y²) = (x²)² – (y²)² = x⁴ – y⁴.

Question 4.
Fill In the blanks given in the table with suitable answers.

Solution:

Question 5.
Find the remainder when x³ + 1 is divided by (x + 1) by using division method.
Solution:

Remainder = 0

Question 6.
What are the possible polynomial expressions for dimensions of the cuboid whose volume is x³ – x ?
Solution:
Volume of cuboid = x³ – x
By splitting x³ – x as factors
x³ – x = x(x² – 1) = x(x + 1) (x – 1)
Possible dimensions of cuboid are x, (x + 1) and (x – 1)

Question 7.
Write the polynomial in ‘x’ whose zeroes are 1, 2 and – 1.
Solution:
The given zeroes of polynomials in ‘x’ are : 1, 2 and – 1.
The factors of the polynomial are : x – 1, x – 2 and x + 1
The required polynomial is : (x – 1) (x – 2) (x + 1)
= (x² – 1) (x – 2) = x³ – 2x² – x + 2.

Question 8.
The polynomial p(x) = x⁴ – 2x³ + 3x² – ax + 3a – 7 when divided by x + 1 leave the remainder 19. Find the value of “a”. Also find the remainder when p(x) is divided by x + 2.
Solution:
Given polynomial = p(x) = x⁴ – 2x³ + 3x² – ax + 3a – 7
When p(x) is divided by (x + 1) leaves the remainder is 19.
∴ p(-1) = 19
p(-1) = (-1)⁴ – 2(-1)³ + 3(-1)² – a(-1) + 3a – 7 = 19
⇒ 1 + 2 + 3 + a + 3a – 7 = 19
⇒ 4a – 1 = 19
⇒ 4a = 20
⇒ a = 20 ÷ 4 = 5
p(x) = x⁴ – 2x³ + 3x² – 5x + 8
p(x) is divided by (x + 2), then p(-2). P(-2) = (-2)⁴ – 2(-2)³ + 3(-2)² – 5(-2) + 8
= 16 + 16 + 12 + 10 + 8 = 62
Required remainder = 62.

Question 9.
In ABC, E and F are mid points of sides AB and AC respectively then prove that i) EF // BC and ii) EF = \(\frac{1}{2}\) BC
Solution:
Given : B and F are mid points of AB and AC.

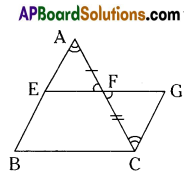
R.T.P. : i) EF // BC, ii) EF = \(\frac{1}{2}\) BC
Construction: GC // AB, extend EF upto G.
Proof:
ΔAEF ΔCGF
∠AFE = ∠CFG (Vertically opposite angles)
AF = FC
∠EAF = ∠GCF (Alternate angles)
∴ ΔAEF ≅ ΔCGF
∴ CG = BE and CG // BF (Constrution)
∴ EBCG is a parallelogram.

Question 10.
Read the following table and answer the following questions given below.

i) The point belongs to Q₃
if) The abscissa of the point C
iii) The point lie on X – axis
iv) The coordinates of origin
v) The point satisfy x > 0, y < 0
vi) The point satisfy x – y = 1
vii) The position of point B
viii) The Quadrant contain (3, – 2)
Solution:
i) D
ii) 3
iii) F, H
iv) 0,0
v) C (3, – 2)
vi) A (2, 1)
vii) Positive Y- axis
viii) Q₄

Question 11.
i) Verify that
p³ + q³ + r³ – 3pqr = (p + q + r)
(p² + q² + r² – pq – qr – rp)

ii) If a + b + c = 0, then prove that a³ + b³ + c³ = 3abc.
Solution:
i) RHS = (p + q + r)
(p² + q² + r² – pq – qr – rp)
= p(p² + q² + r² – pq – qr – rp) + q (p² + q² + r² – pq – qr – rp) + r (p² + q² + r² – pq – qr – rp)
= p³ + pq² + pr² – p²q – pqr – p²r + p²q + q³ + qr² – pq² – q²r – pqr + p²r + q²r + r³ – pqr – qr² – r²p
= p³ + q^{3</sup + r3 – pqr – pqr – pqr
= p3 + q3 + r3 – 3pqr}

ii) Given a + b + c = 0 ⇒ a + b = -c ……………..(1)

Cubing on both sides
(a + b)³ = (-c)³
a³ + b³ + 3ab (a + b) = -c³
a3 + b3 + 3ab (-c) =-c3 {From(l)}
a³ + b³ – 3abc = -c³
a³ + b³ + c³ – 3abc

Question 12.
If both (x – 2) and (x – \(\frac{1}{2}\)) are factors of px² + 5x + q, show that p = q.
Solution:
Let f(x) = px² + 5x + q, if (x – 2) is the factor of f(x)
⇒ f(2) = p(2)² + 5 × 2 + q = 0
⇒ 4p + 10 + q = 0 ……………. (1)
If (x – \(\frac{1}{2}\) ) is the factor of f(x)
f(\(\frac{1}{2}\)) = P(\(\frac{1}{2}\))² + 5 × \(\frac{1}{2}\) + q = 0
⇒ \(\frac{\mathrm{p}}{4}+\frac{5}{2}\) + q = 0
⇒ p + 10 + 4q = 0 ……………. (2)
from (1) and (2)
⇒ 4p + 10 + q = p + 10 + 4q
⇒ 4p + q = p + 4q
⇒ 4p – p = 4q – q
⇒ 3p = 3q
⇒ p = q

Question 13.
If ax² + bx + c and bx² + ax +-c have a common factor (x + 1) then show that a = b and c =’0.
Solution:
Given that (x + 1) is the factor of f(x) = ax² + bx + c
⇒ f(- 1) = a(- 1)² + b(- 1) + c = 0
⇒ a – b + c = 0 …………….. (1)
(x + 1) is the factor of f(x) = bx² +, ax + c
f(- 1) = b(- 1)² + a(- 1) + c = 0
⇒ b – a + c = 0 …………… (2)
from (1) and (2)
a – b + c = b – a + c
⇒ a – b = b – a
⇒ a + a = b + b
⇒ 2a = 2b
∴ a = b
if a = b, from equation (1)
c = 0