AP 9th Class Maths Important Questions Chapter 1 Real Numbers

These AP 9th Class Maths Important Questions 1st Lesson Real Numbers will help students prepare well for the exams.

AP State Syllabus 9th Class Maths 1st Lesson Important Questions and Answers Real Numbers

Question 1.
Represent \(\frac{-13}{5}\) on number line.
Solution:
Draw number line, having, -3, -2, -1,0, 1 integers on it.

→ Divide each unit as 5 equal parts on either side of zero.
→ From these count 13 parts on left side of the zero, which indicates \(\frac{-13}{5}\)

Question 2.
Find any two irrational numbers between 0.5 and 0.55.
Answer:
Two irrational numbers between 0.5 and 0.55 are (0.52515345 ……………….. and
0.541656475 …………….. ).

Question 3.
Simplify (25)^3/2 × (625)^-1/4
Solution:
Given that (25)^3/2 × (625)^-1/4
= (5²)^3/2 × (5⁴)^-1/4
= \(5^{2 \times \frac{3}{2}} \times 5^{4 \times\frac{-1}{4}}\) = 5³ × 5^-1 = 5^3-1 = 5² – 25.

Question 4.
Find two rational numbers between 0.2 and 0.3.
Solution:
The rational numbers between 0.2 and 0.3 is 0.25 and 0.28.
It means \(\frac{25}{100}, \frac{28}{100}=\frac{1}{4}, \frac{7}{25}\)

Question 5.
Convert \(\sqrt[3]{5}\) from the radical form to the exponential form.
Solution:
As \(\sqrt[n]{a^{m}}=(a)^{\frac{m}{n}}\) = \(\sqrt[n]{a}=(a)^{\frac{1}{n}}\)
\(\sqrt[3]{5}=(5)^{\frac{1}{3}}\)

Question 6.
Find the value of \(\text { (625) } \frac{-1}{4} \text { . }\) .
Solution:

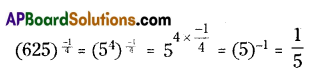
Question 7.
Simplify: \(\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{3}-\sqrt{2}}\)
Solution:

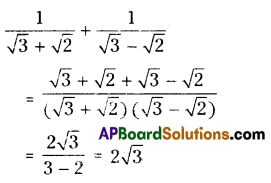
Question 8.
Prove that if x is odd, then x² is also odd.
Solution:
x is an odd number, x = 2k + 1
{definition of odd}
x = 2k + 1
squaring on both sides
(x)² = (2k + 1)²
x² = 4k² 4k + 1 = 2(2k² + 2k) + 1 = 2l + 1
x² = 2l + 1 {l = 2k² + 2k}
∴ x² is an odd number.

Question 9.
Express \(5 . \overline{25}\) in from where q ≠ 0, p and q are co primes.
Solution:
Let x = \(5 . \overline{25}\)
x – 5.25 25 25 ……………… (1)
Multiply by 100 to (1)
100 x = 525.25 25 25 ………….. (2)
Subtract (1) from (2)

Question 10.
Express as a decimal number.
Solution:
For the correct process of division.
For expressing = 0.5222222 …………
= \(0.5 \overline{2}\)

Question 11.
If = a + b√3, then find the value of a³ + b³
The Rationalising Factor of 7 – 4√3 and √3 – 2 is 7 + 4√3 and √3 + 2

= 7 + 4√3 – √3 – 2
= 5 + 3√3 = a + b√3
Here a = 5,b = 3
∴ a³ + b³ = (5)³ + (3)³ = 125 + 27 = 152

Question 12.
Visualize the value of √5 upto 3 decimals on a number line, using successive magnification.
Solution:

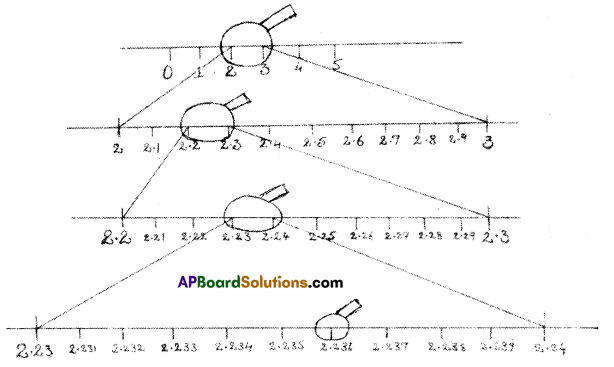
Question 13.
If x = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\) and y = \(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}\), then find the value of x² + y².
Solution:
Given that x = \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}\)
R.F. of √3 – √2 is √3 + √2

x² + y² = (5 + 2√6 )² + (5 – 2√6 )²
= 25 + 20√6 + 24
+ 25 – 20√6 + 24
= 98

Question 14.
If √2 = 1.414, √3= 1.732, then find then value of \(\frac{4}{3 \sqrt{3}-2 \sqrt{2}}+\frac{3}{3 \sqrt{3}+2 \sqrt{2}}\).
Solution:
Given that √2 = 1.414 and √3 = 1.732

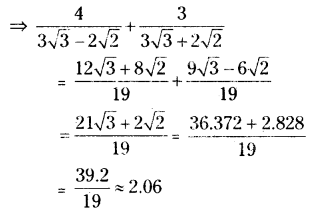
Question 15.
If \(\frac{5+2 \sqrt{3}}{7+4 \sqrt{3}}\) = a + b√3, then find the values of a and b.
Solution:
Given that \(\frac{5+2 \sqrt{3}}{7+4 \sqrt{3}}\)
Now rationalise the denominator, (Rational Factor of 7+4√3 is 7 – 4√3 )
= \(\frac{5+2 \sqrt{3}}{7+4 \sqrt{3}} \times \frac{7-4 \sqrt{3}}{7-4 \sqrt{3}}\)
= \(\frac{35-20 \sqrt{3}+14 \sqrt{3}-8 \times 3}{(7)^{2}-(4 \sqrt{3})^{2}}\)
= \(\frac{11-6 \sqrt{3}}{49-48}\) = 11 – 6√3
a + b√3 – 11 – 6√3 =11 + (-6)√3
.’. a = 11, b = -6.

Question 16.
Visualise \(4.6 \overline{7}\) on number line upto 3 decimal places, using successive magnification.
Solution:

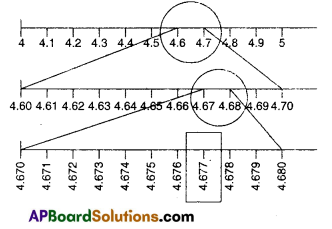
Question 17.
Represent -√3 and √3 on number line.
Solution:

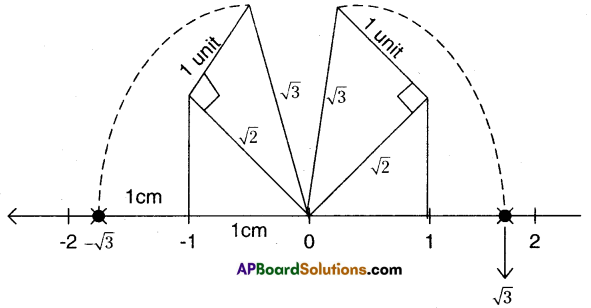
Question 18.
Find the value of ‘a’ and ‘b’, if \(\frac{(\sqrt{5}-\sqrt{3})}{2 \sqrt{5}+3 \sqrt{3}}\) = a + b\(\sqrt{15}\)
Solution:
The Rationalising Factor of \(\frac{(\sqrt{5}-\sqrt{3})}{2 \sqrt{5}+3 \sqrt{3}}\)
is 2√5 – 3√3 , multiplying the numerator and denominator with 2√5 – 3√3.

Question 19.
Represent 2.019 on number line using the method of successive magnification.
Solution:

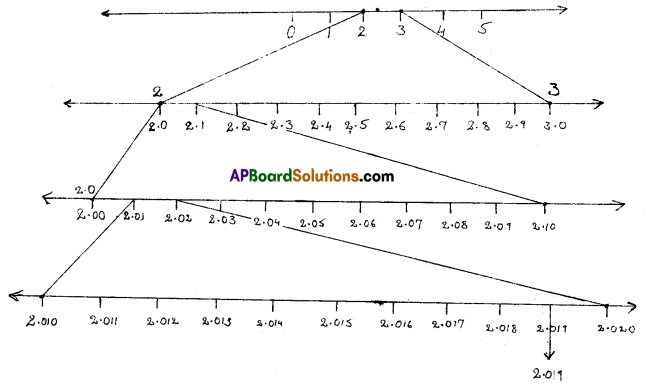
Question 20.
Simplify:
\(15 \sqrt[5]{32}+\sqrt{225}-8 \sqrt[3]{343}+\sqrt[4]{81}\)
Solution:
= \(15 \sqrt[5]{32}+\sqrt{225}-8 \sqrt[3]{343}+\sqrt[4]{81}\)
= \(15 \sqrt[5]{2^{5}}+\sqrt{15^{2}}-8 \sqrt[3]{7^{3}}+\sqrt[4]{3^{4}}\)
= (15 × 2) + 15 – (8 × 7) + 3
= 30 + 15 – 56 + 3 = – 8.

Question 21.
Express \(5.12 \overline{3}\) in \(\frac{\mathbf{p}}{\mathbf{q}}\) form where p and q are co-primes.
Solution:
Let x = \(5.12 \overline{3}\)
=> x = 5.12333 ……………. (1)
Here periodicity is 1.
So, we have to multiply (1) with 10.on both sides.
=> 10 × x = 10 × 5.12333 ……………….
10 x = 51.2333. …………… (2)
(2) – (1)

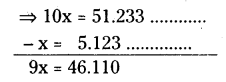
x = \(\frac{46.11}{9}=\frac{46.11}{9}\) × \(\frac{100}{100}=\frac{4611}{900}\)
∴ x = \(\frac{4611}{900}\)

Question 22.
The length of a rectangular field is \(\sqrt[3]{5}+\sqrt[3]{2}\) Find the measure of its breadth such that the area of the rectangle is a rational number.
Solution:
Given that the length of a rectangular
field (l) = \(\sqrt[3]{5}+\sqrt[3]{2}\).
If we want to get area of rectangle as a rational number, then we should take the breadth as Rationalising Factor of length.

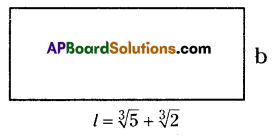
Question 23.
Simplify:
\(\sqrt[4]{81}-8 \cdot \sqrt[5]{243}+15 \cdot \sqrt[5]{32}+\sqrt{225}\)
Solution:
\(\sqrt[4]{81}-8 \cdot \sqrt[5]{243}+15 \cdot \sqrt[5]{32}+\sqrt{225}\)
= \(\sqrt[4]{3^{4}}-8 \cdot \sqrt[5]{3^{5}}+15 \cdot \sqrt[5]{2^{5}}+\sqrt{15^{2}}\)
= \(\left(3^{4}\right)^{\frac{1}{4}}-8 \cdot\left(3^{5}\right)^{\frac{1}{5}}+15\left(2^{5}\right)^{\frac{1}{5}}+\left(15^{2}\right)^{\frac{1}{2}}\)
= 3 – 8.3 + 15.2 + 15
= 3 – 24 + 30+ 15
= 48 – 24 = 24