These AP 10th Class Maths Chapter Wise Important Questions Chapter 9 Tangents and Secants to a Circle will help students prepare well for the exams.
AP State Syllabus 10th Class Maths 9th Lesson Important Questions and Answers Tangents and Secants to a Circle
Question 1.
What do we call the part a and b in the below circle ?

Solution:
‘a’ is minor segment and ‘b’ is major segment.
Question 2.
Find the length of the tangent to a circle of radius 7 cm at a point from a distance 25 cm from the centre.
Solution:
Given OA = 25 cm, OB = r = 7 cm
In ΔAOB, ∠B = 90°
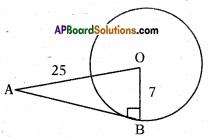
OA2 = OB2 + AB2
⇒ AB2 = OA2 – OB2 = 252 – 72
⇒AB = \(\sqrt{25^{2}-7^{2}}=\sqrt{625-49}\)
= \(\sqrt{576}\)
= 24 cm
Question 3.
Find the area of a sector of a circle whose radius is 7 cm and angle at the centre is 60°.
Solution:
Radius = 7 cm, Angle at centre = 60°
Area of the sector = \(\frac{\mathrm{x}}{360}\) x πr²
= \(\frac{60 \times \frac{22}{7} \times 7 \times 7}{360}=\frac{154}{6}\) = 25.66 cm2
![]()
Question 4.
A tangent is drawn to a circle of radius 4 cm. from a point that lies at a distance of 5 cm. from the centre. Find the measure of length of the tangent.
Solution:
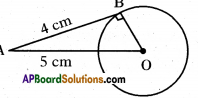
ΔOAB is a right triangle.
OA2 = 0B2 + AB2
52 = OB2 + 42
OB2 = 25 -16 = 9
OB = \(\sqrt{9}\) = 3 cm.
Question 5.
Find the area of the shaded part in the given figure.
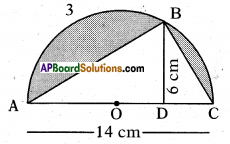
Solution:
Area of shaded part
= Area of semi-circle – Area of triangle

Question 1.
Find the length of the tangent from a point 13 cm away from the centre of the circle of radius 5 cm.
Solution:
Radius of the circle = 5 cm
Length of the tangent = x cm
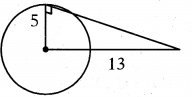
Distance between centre to point be = 13 cm
132 = 52 + x2
x2 = 169 – 25 = 144 ⇒ x = 12 cm
Question 2.
If tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at angle of 80°, then find the measured of ∠POA.
Solution:
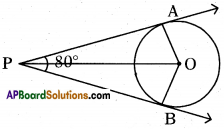
Between ΔA0P and ΔB0P
∠OAP = ∠OBP = 90° (∵ tangent and line from origin meet at 90° to each other)
0A=0B = radius of the circle = r (say)
and OP is the common side
Hence, we can say ΔAOP = ΔBOP
Therefore, we can say
∠OPA = ∠OPB = \(\frac { 1 }{ 2 }\)(∠APB)
= \(\frac { 1 }{ 2 }\)(80°) = 40°
(∵ given that tangents PA and PB are inclined to each other by 80°)
Now, in ΔAOP,
∠POA + ∠OPA + ∠A = 180°
⇒ ∠POA + 40° + 90° = 180°
⇒ ∠POA = 50°
Question 3.
Draw a circle of radius 3 cm, mark a point ‘P’ on the circle and draw a tan gent at ‘P’.
Solution:
Steps of construction:
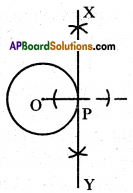
1) Draw a circle of radius ‘3’ cm from the centre “O” and pick a point ‘P’ on the circle. Join \(\overline{\mathrm{OP}}\)
2) Now draw a perpendicular at the point ‘P’ to the line segment \(\overline{\mathrm{OP}}\)
such that XY ⊥ \(\overline{\mathrm{OP}}\).
3) Then \(\overline{\mathrm{XY}}\) is the desired tangent at ‘P’ to the given circle.
Question 4.
A chord of a circle of radius 10 cm. subtends a right angle at the centre. Find the area of the corresponding minor segment (use π = 3.14),
Solution:
Radius of circle (r) = 10 cm
Sector angle (x) = 90°
Radius of sector (r) = 10 cm.
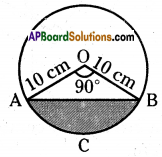
Area of sector OACB = \(\frac{\mathrm{x}}{360}\) × πr²
= \(\frac{90^{\circ}}{360^{\circ}}\) × 3.14 × 10 × 10
= 78.5 Sq. cm
Area of Δ AOB = \(\frac { 1 }{ 2 }\) × 10 × 10
= 50 cm2
Area of the Minor Segment = Area of sector OACB – Area of Δ OAB
= 78.5 – 50.0 = 28.5 cm2
![]()
Question 1.
A chord of circle of radius 10 cm sub-tends a right angle at the centre. Find the area of the corresponding :
i) Minor segment ii) Major segment (use π = 3. 14)
Solution:
Radius of circle (r) = 10 cm
Sector angle (x) = 90°
Radius of sector (r) = 10 cm.
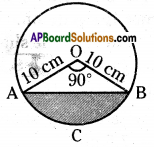
Area of sector OACB = \(\frac{\mathrm{x}}{360}\) × πr2
= \(\frac{90^{\circ}}{360^{\circ}}\) × 3.14 × 10 × 10
= 78.5 Sq. cm
Area of ∆ AOB = \(\frac { 1 }{ 2 }\) × 10 × 10
= 50 cm2
Area of the Minor Segment = Area of sector OACB – Area of ∆ OAB
= 78.5 – 50.0 = 28.5 cm2
Area of Major Segment = Area of the circle – Area of the Minor Segment
= (3.14 × 10 × 10) – 28.5
= 314-28.5 = 285.5 cm2
Question 2.
Draw a circle of radius 3 cm. Take a point ’P’ at a distance of 5 cm from the centre of the circle. From P, draw 2 tangents to the circle.
Solution:
Award marks for construction as follows:
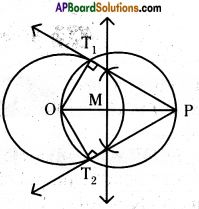
i) To draw a circle with radius 3 cm
ii) To plot a point P such that OP = 5 cm.
iii) To Bisect QP at M and draw circle with radius OM br MP
iv) To draw tangents from intersecting points of two circles.
Question 3.
Draw a Circle of radius 4 cm. From a point 7.5 cm away from its centre, construct the pair of tangents to the circle.
Solution:
1) Draw a circle with:radius 4 cm with centre O.
2) Locate a point P such that OP 7.5 cm
3) Bisect OP and draw circle with radius MO or MP with centre M.
4) Draw tangents PA and PB from external point P to the given circle.
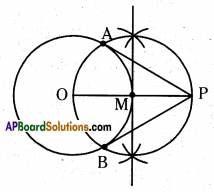
Question 4.
Draw a circle of radius 5 cm. From a point 8 cm away from its centre, con-struct a pair of tangents to the circle. Find the lengths of tangents.
Solution:
Steps of construction :
1) Construct a circle with a radius of 5 cm.
2) Trace the point ‘p’ in the exterior of the circle which is at a distance of ‘8’ cm from its centre.
3) Construct a perpendicular bisector to OP which meets at M.
4) The draw a circle with a radius of MP or MO from the point M. This circle cuts the previous circle drawn from the centre ‘O’ at the points A and B.
5) Now join the points PA and then PB.
6) PA, PB are the required tangents which are measured 6.2 cm long.
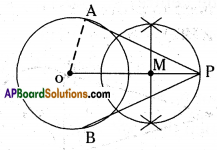
OA = 5 cm ; OP = 8 cm
AP = PB = 6.2 cm.
Question 5.
Draw a circle of radius 4 cm and draw a pair of tangents to the circle, which are intersecting each other 6 cm away from the centre.
Solution:
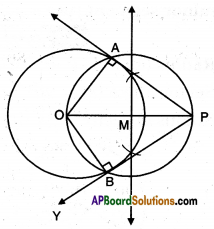
Steps of Construction:
1) Draw a circle with centre ‘O’ and radius 4 cm.
Take a point ‘P’ outside the circle such that OP = 6 cm. Join OP.
Draw the perpendicular bisector to OP which bisects it at M.
4) Taking M as centre and PM or MO as radius draw a circle.
Let the circle intersects the given circle at ’A’ and ‘B’.
Join P to A and B.
PA and PB are the required tangents of lengths.
Question 6.
Two tangents TP and TQ are drawn to a circle with centre ‘O’ from an external point T, then prove that ∠PTQ = 2. ∠OPQ.
Solution:
Given a circle with centre 0.
Two tangents TP, TQ are drawn to the circle from an external point T.
We need to prove ∠PTQ = 2∠OPQ
Let ∠PTQ = θ
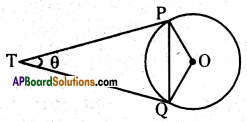
TP = TQ (The lengths of tangents drawn from an external point to a circle are equal)
So ΔTPQ is an isosceles triangle
∴ ∠TPQ + ∠TQP + ∠PTQ = 180°
(Sum of three angles in a triangle)
∠TPQ = ∠TQP = \(\frac { 1 }{ 2 }\)(180° – θ)
= 90°- \(\frac{\theta}{2}\)
∠OPQ = ∠OPT – ∠TPQ
= 90° – 0(90° – \(\frac{\theta}{2}\)) = \(\frac{\theta}{2}\)
= \(\frac { 1 }{ 2 }\) ∠PTQ
∴∠PTQ = 2∠OPQ
![]()
Question 7.
Find the area of the segment shaded in the figure in which PQ = 12 cm, PR = 5 cm and QR is the diameter of the circle with centre ‘O’. (Take π = \(\frac{22}{7}\))
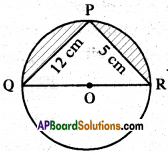
Solution:
To find the area of the segment shaded in the given figure.
Here ‘PQ’ = 12 cm; ‘PR’ = 5 cm; ‘QR’ is diameter
Now PQOR is a semicircle then angle in a semicircle is 90°.
then ∠QPR = 90°
∴ ΔPQR is a right angled triangle
∴ Area of ΔPQR = \(\frac { 1 }{ 2 }\) bh
= \(\frac { 1 }{ 2 }\) × PQ × PR
= \(\frac { 1 }{ 2 }\) × 12 × 5 =30 cm2 ……………(1)
Now the area of shaded part = area of semicircle – area of ΔPQR
= \(\frac { 1 }{ 2 }\)πrcm2 – 30 cm2 …………….(2)
In ΔPQR, QR2 = PQ2 + PR2
(from Pythagoras theorem)
QR2 = 122 + 52
= 144 + 25 = 169 = 132
∴ QR =13 then
Radius of the circle (r) = QO = \(\frac{\mathrm{Q} R}{2}\)
= \(\frac{13}{2}\) = 6.5 cm
then area of semicircle
= \(\frac { 1 }{ 2 }\)πrcm2
= \(\frac{1}{2} \times \frac{22}{7} \times \frac{13}{2} \times \frac{13}{2}\) = 66.39 cm2 …………….(3)
Now putting the values of (1) and (3) in (2) we get
Area of shaded part = (66.39 – 30)
= 36.39 cm2.
Question 8.
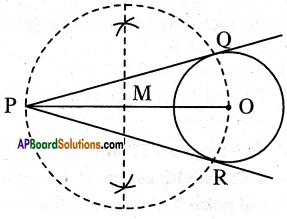
Draw two tangents to a circle of radius 2.5 cm, from a point ‘P’ at a distance of 7 cm from its centre.
Solution:
1. Draw a line segment PO = 7 cm.
2. From the point O, draw a circle of radius = 2.5 cm.
3. Draw a perpendicular bisector of PO. Let M be the mid-point of PO.
4. Taking M as centre and OM as radius, draw a circle.
5. Let this circle intersects the given circle at the point Q and R.
6. Join PQ and PR.
Question 1.
As shown in the figure, radius of the given circle is 21 cm and ∠AOB = 120°. Then find the area of segment AYB.

Solution:
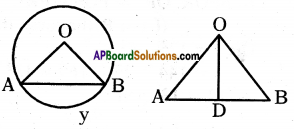
Given radius of area = OA = OB = 21 cm
Now3 the angle at centre for the sector \(\widehat{\mathrm{OAB}}\) = 120°.
Formula for area of sector = \(\frac{x}{360}\) x πrcm2
= \(\frac{120}{360} \times \frac{22}{7}\) × 21 × 21
= 22 × 21 = 462 cm2 ……………………… (1)
Now area of segment \(\widehat{\mathrm{AYB}}\)
= Area of sector – area of Δ OAB.
Let \(\overline{\mathrm{OD}}\) is perpendicular to AB, then
∠AOB = \(\frac{120}{2}\) = 60°
∴ sin 60° = \(\frac{\mathrm{AD}}{\mathrm{OA}}\)
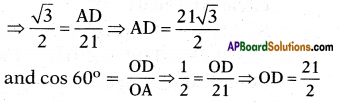
∴ area of ΔOAB = \(\frac { 1 }{ 2 }\) bh
= \(\frac { 1 }{ 2 }\) × AB × OD = AD × OD
= \(\) = 190.95 cm2 ………….. (2)
∴ area of segment \(\widehat{\mathrm{AYB}}\)
= 462 – 190.95
= 271.05 cm2
= 271.05 cm2
![]()
Question 2.
In a wall clock, length of minutes needle is 7 cm. Then find the area covered by it in 10 minutes of time.
Solution:
Length of minutes needle =(r) = 7 cm
We need to calculate the area covered by in 10 minutes of time = Area of sector.

Now the angle covered by it in 60 minutes = 360°
∴ In 10 minutes = \(\frac{360}{60} \) × 10 = 60°
Area of sector = \(\) × 7 × 7
= \(\frac{154}{6}=\frac{77}{3}\)
∴ Area covered by it in 10 minutes of time = \(\frac{77}{3}\) cm2 = 25.66 cm2
Question 3.
Find the area of a right hexagon inscribed in a circle having 14 cm of radius.
Solution:
Radius of circle = OA = OB = OC = OD = OE = OF = 14 cm
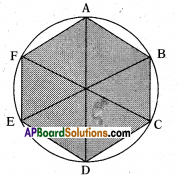
∠AOB = \(\frac{360}{6} \) = 60°
∴ In ΔAOB AO = BO = 14 cm
∠AOB = 60°
then ∠OAB = ∠OBA
(∵ Opposite to equal sides)
And ∠OAB + ∠OBA + 60 = 180
=> ∠OAB = ∠OBA = ∠AOB = 60°
Hence it is an equilateral triangle.
∴ OA = OB = AB = 14 cm
∴ Area of hexagon = 6 (Area of ΔAOB)
= 6. \(\frac{\sqrt{3}}{4}\) a2
= 6. \(\frac{\sqrt{3}}{4}\) × 14 × 14
Area of hexagon = 294\(\sqrt{3}\) cm2
Question 4.
Four carrorp board pans are arranged as shown in figure. Radius of the pan is 3 cm each. Then find the area in between of them.
Solution:
Area in between 4 pans = Area of square ABCD formed by joining their centres – 4 (area of sector)
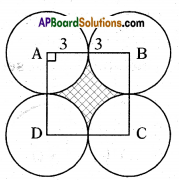
Now side of square ABCD = 3 + 3 = 6
Then area of square ABCD
= 6 × 6
= 36 cm2
and now area of sector = \(\frac{x}{360}\) × πr2
Area of 4 sectors
= 4 × \(\frac{90}{360} \times \frac{22}{7}\) × 3 × 3
= \(\frac{198}{7}\) = 28.3 cm2
∴ Area in between 4 pans i.e., shaded
= 36 – 28.3 = 7.7 cm2
