AP 10th Class Maths Important Questions Chapter 7 Coordinate Geometry

These AP 10th Class Maths Chapter Wise Important Questions Chapter 7 Coordinate Geometry will help students prepare well for the exams.

AP State Syllabus 10th Class Maths 7th Lesson Important Questions and Answers Coordinate Geometry

Question 1.
What do you mean by centroid of a triangle ?
Solution:
“The concurrent point of medians of a triangle is called centroid of the triangle”.

Question 2.
Find the co-ordinates of the point, which divides the line segment joining (2, 0) and (0, 2) in the ratio 1:1.
Solution:
x₁ = 2 ; x₂ = 0 ; y₁ = 0 ; y₂ = 2
Point divides the line segment joining (2,0) and (0, 2) in the ratio 1 : 1

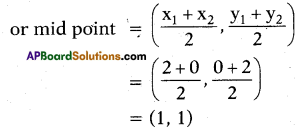
Question 3.
Find the distance between (a cos θ, 0) and (0, a sin θ).
Solution:
To find the distance between the points (a cos θ, 0) and (0, a sin θ) we use the formula.
\(\sqrt{\left(\mathrm{x}_{1}-\mathrm{x}_{2}\right)^{2}+\left(\mathrm{y}_{1}-\mathrm{y}_{2}\right)^{2}}\)
Where x₁ = 0, y₁ = a sin θ and
x₂ = a cos θ, y₂ = 0
∴ The distance between above given two points

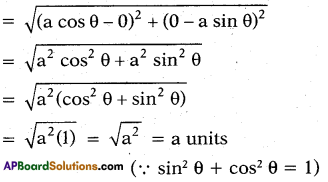
Question 4.
If A(4,0), B(0, y) and AB = 5, find the possible values of y. d
Solution:
A(4,0), B(0, y) and AB = 5
\(\) = 5
\(\) = 5
16 + y² = 2
y² = 25 – 16 = 9
y = ± \(\sqrt{9}\) = ± 3
Possible values of y are 3 or – 3.

Question 5.
Find the radius of the circle with cen¬tre (3, 2) and passes through (4, – 1).
Solution:

Question 6.
Let the 3 vertices of a triangle ABC are A(3, -2), B(-5, 4) and C(2, – 2). What do you observe for the centroid of this triangle ?
Solution:
centroid of this triangle
= \(\left(\frac{\mathbf{x}_{1}+\mathrm{x}_{2}+\mathrm{x}_{3}}{3}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}+\mathrm{y}_{3}}{3}\right)\)
= \(\left(\frac{3+(-5)+2}{3}, \frac{-2+4+(-2)}{3}\right)\) = (0,0)
Observed that the centroid is the origin.

Question 7.
Find the centroid of a triangle, whose vertices are (6, 2), (0, 0) and (4, -5).
Solution:

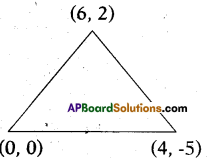
Given vertices are (6, 2) (0, 0) and (4, -5) then centroid

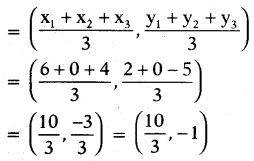
Question 8.
Find the radius of the circle whose cen-tre is (3, 2) and passes through (- 5, 6).
Solution:
Given : A circle with centre A (3, 2) passing through B (- 5, 6).

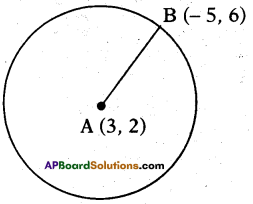
Radius = AB
[ ∵ Distance of a point from the centre of the circle]
Distance formula

Question 9.
What is the distance between (0, – sin x) and (- cos x, 0) ?
Solution:
Distance between (0, – sin x) and (- cos x, 0)

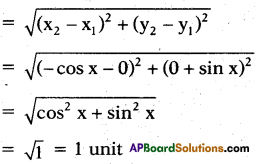
Question 10.
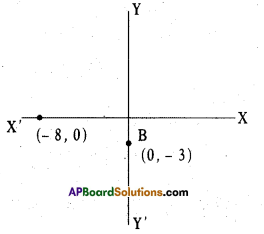
Where do the points (0, -3) and (-8, 0) lie on co-ordinate axis ?
Solution:
The point (0, – 3) lie on OY
∵ Its x co-ordiante is zero and
y – coordinate is negative.
and the point (-8, 0) lie on OX’
∵ Its y – cordinate is zero and
x-cordinate is negative.

Question 11.
Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution:
Let P(x, y); A(7, 1); B(3, 5)
The distance between points (x₁, y₁) and (x₂, y₂) is

by the sum, PA = PB

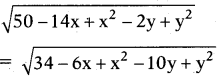
50 – 14x + x² – 2y + y²
= 34 – 6x + x² – 10y + y²
50 – 14x – 2y – 34 + 6x 4- 10y = 0
-8x + 8y + 16 = 0
-x + y + 2 = 0 ,
∴ x = y + 2

Question 12.
Find the value of k, for which the points (7, 2), (5, 1) and (3, k) are collinear.
Solution:
The area of the triangle formed by those points = 0
Area of the triangle
\(\frac { 1 }{ 2 }\){x₁(y₂-y₃) + x₂(y₃-y₁)
+ x₃(y₁ – y₂)} = 0
\(\frac { 1 }{ 2 }\)|7(1 – k) + 5(k – 2) + 3(2 – 1)| = 0
\(\frac { 1 }{ 2 }\) |-2k| = 0
∴ k = 0

Question 13.
Find the centroid of the triangle, whose vertices are (-4, 4), (-2, 2) and (6,-6).
Solution:
Centroid of the triangle

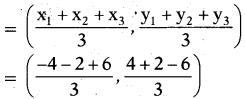
= (0,0)

Question 14.
If the distance between two points (x, 1) and (-1,5) is ‘5’, find the value of V.
Solution:
Given points (x, 1) and (-1, 5)
Let A (x, 1) and B (-1, 5)
Distance between

Now, squaring on both sides (-1 -x)² + 16 = 25
(-1 – x)² = 25- 16 = 9
(-1 – x)² = 3²
-1 – x = 3
-1 – 3 = x ⇒ x = -4

Question 15.
Verify whether the following points are collinear or not.
(1,-1), (4, 1), (-2,-3)
Solution:
To show that three points are collinear the area formed by the triangle is zero.
Given points are (1, -1), (4, 1), (-2, -3) Formula for area of triangle
A = \(\frac { 1 }{ 2 }\){x₁(y₂-y₃) + x₂(y₃-y₁)
= \(\frac { 1 }{ 2 }\)|1(1 +3) + 4(-3 + 1)
-2 (-1-1)1
= \(\frac { 1 }{ 2 }\)|4-8 + 4|.
= \(\frac { 1 }{ 2 }\) |8 – 8| = \(\frac { 1 }{ 2 }\)|0| = 0
So the given three points are collinear.

Question 16.
Find the area of a triangle, whose sides are 5 cm, 12 cm and 13 cni, by using Heron’s formula.
Solution:
Let a = 5 cm; b = 12 cm; :c =13 cm
s= \(\frac{a+b+c}{2}=\frac{5+12+13}{2}\) = 15
Area of triangle
(Δ) = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15(15-5)(15-12)(15-13)}\)
= 30 cm²

Question 17.
Find out whether the points (1,5), (2, 5) and (-2,-1) are collinear using the distance formula.
Solution:
A(1, 5), B(2, 5), C(- 2,-1)
Distance formula,

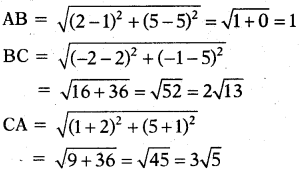
Question 18.
Read the following graph and answer the questions given below.

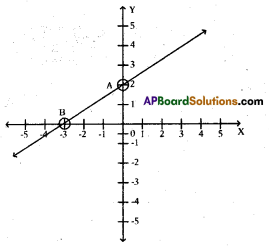
i) Write the coordinates of the points A and B.
ii) What is the slope of the line \(\overline{\mathbf{A B}}\) ?
Solution:

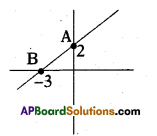
i) Coordinates of
point ‘A’ = (0, 2)
point B = (-3, 0)

ii) Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{0-2}{-3-0}=\frac{-2}{-3}=\frac{2}{3}\)

Question 19.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
Solution:

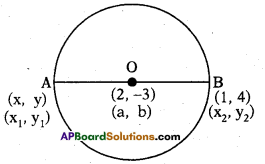
Question 20.
Check whether the points (3, 0), (6,4) and (—1, 3) are the vertices of a right – angled isosceles triangle or not. Also find the area of the triangle.
Solution:
Distance between A(3, O), B(6, 4)

∴ AB² = 25, BC² = 50, CA²= 25
BC² = AB² + CA² and AB = CA
∴ ∆ ABC is an Isosceles right angled triangle
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) x AB x AC
= \(\frac { 1 }{ 2 }\) x 5 x 5 = 12.5sq.u

Question 21.
Find the area of the triangle formed by the points (2, 3), (- 1, 3)and (2,-1) using Heron’s formula.
Solution:
To find the area of the triangle formed by (2, 3) (- 1, 3) and (2,-1) using Heron’s formula.
Let the co-ordinates of A = (2, 3) ; B = (- 1, 3); C = (2, – 1) then the sides of AABC are represented by as follows

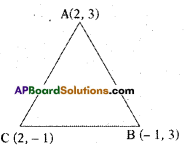
AB = c, BC = a, CA = b then the formula of the triangle using Heron’s formula
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
where s = \(\frac{a+b+c}{2}\)
Now, we find the sides of ∆ABC, using the formula \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
∴ CB = a = distance between the points (2, – 1) and (-1,3)

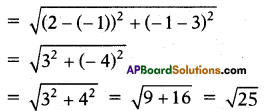
⇒ CB = a = 5 ………………..(1) .
and AB = c the distance between (-1,3) and (2, 3)

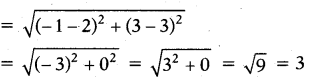
∴ AB = c = 3 …………………..(2)
and AC = b the distance between A(2, 3) and C(2, – 1)

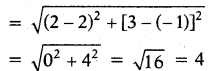
AC = b = 4 …………..(3)

∴ Area of above triangle = 6 sq.units.

Question 22.
If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a paral-lelogram, taken in order, then
i) find the value of p.
ii) find the area of ABCD.
Solution:
i) A, B, C, D are the vertices of a parallelogram
Mid point of AC =- Mid point of BD

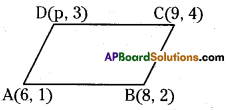
A(6, 1) = (x₁, y₁); C(9, 4) – (x₂, y₂)

ii) ar ΔABC = \(\frac { 1 }{ 2 }\)| x₁ (y₂ – y₃) + x₂(y₃ – y₁)
+ x₃ (y₁ -y₂)|
= \(\frac { 1 }{ 2 }\)|6(2 – 4) + 8(4 – 1) + 9(1 – 2)|
= \(\frac { 1 }{ 2 }\) |-12+24-9|
= \(\frac { 1 }{ 2 }\) |3
= \(\frac { 3 }{ 2 }\)|sq. units.
∴ Area of parallelogram ABCD = 2 x ar AABC 3
= 2 × \(\frac { 3 }{ 2 }\) = 3 sq. units.

Question 23.
Find the value of ‘k’ for which the points (3k – 1, k – 2), (k, k – 7) and (k – 1, -k -2) are collinear.
Solution:
Given points are collinear
Let A (3k – 1, k – 2), B (k, k – 7) and
C (k – 1, -k – 2) are on the same line \(\overleftrightarrow{L N}\)
Then slope of \(\overline{\mathrm{AB}}\) and slope of \(\overline{\mathrm{AC}}\) should be same (∵ they are collinear) Formula for slope

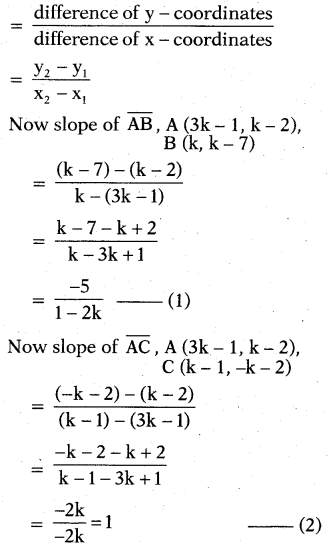
Now (1) = (2)
⇒ \(\frac{-5}{1-2 k}\) = 1
⇒ 1 – 2k = -5
⇒ 1 + 5 = 2k ⇒ 2k = 6
∴ k = 3

Question 24.
Find the co-ordinates of the points of trisection of the line segment joining the points A(2, 1) and B(5, – 8).
Solution:
Let P and Q be the points of trisection of AB, i.e., AP = PQ = QB.

Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordi¬nates of P are (by applying the section formula)

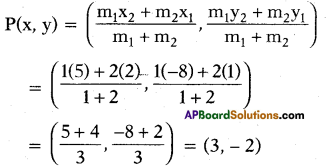
Now, Q also divides AB internally in the ratio 2 : 1. So, the coordinates of Q are

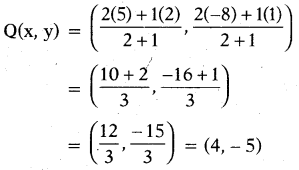
Therefore, the coordinates of the points of trisection of the line segment are P(3, – 2) and Q(4, – 5).

Question 25.
Find the distance between the points (5, 7) and (7, 5).
Solution:
Formula for the distance between the points (x₁, y₁) and (x₂, y₂) is \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
Here (x₁, y₁)=(5,7) and (x₂, y₂) = (7, 5)
∴ The distance between (5, 7) and (7, 5) is

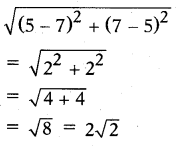
Question 26.
Find the distance between the points (5, 7) and (7, 5) by plotting them in co-ordinate plane with the help of a right angled triangle.
Solution:
A (5, 7), B (7, 5) then O (5, 5)

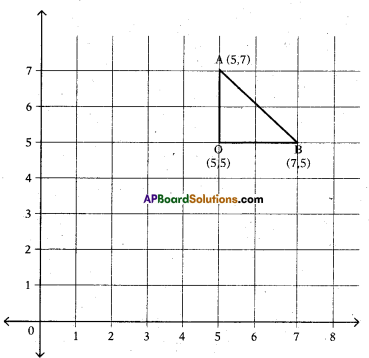
In the ΔAOB, ∠O = 90
∴ AB is hypotenuse.
AO =(7 – 5)= 2
OB = 7 – 5 = 2
Then from Pythagorus theorem

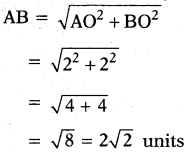
Hence the distance between (5, 7) and (7, 5) = 2\(\sqrt{2}\) units

Question 27.
Are the points (5, 7) and (7, 5) equal ?
Solution:
No, the given points (5, 7) and (7, 5) are not equal.
Why because, the above two points represent two different points in the co-ordinate plane.
So they are not equal.
For (x₁, y₁) = (x₂, y₁) then x₁ must be equal to x₂ and y₁ must be equal to y₂.
So to become (5, 7) = (7, 5)
5 should be equal to 7, which is impossible.
So (5, 7) will not bp equal to (7, 5).

Question 28.
Find the point on X-axis which is equi distant from the points (5, 7) and (7,5).
Solution:
Let the point (p, q) i$ on X-axis, which is equi distant from the points (5, 7) and (7, 5).
As this point (p, q) is on X-axis, its y-coordinate q = 0. Then the point is
(p, 0).
The distance between (5, 7) and (p, 0) is \(\sqrt{(p-5)^{2}+(0-7)^{2}}\) …………… (1)
And the distance between (7, 5) and (p,0) is \(\sqrt{(p-7)^{2}+(0-5)^{2}}\)……………. (2)
The above (1) and (2) are equal.

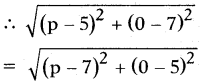
= (p – 5)² + 7²
= (p – 7)² + 5²
= p² – 10p + 25 + 49 = p² – 14p + 49 + 25
∴ -10p + 14p = 0
⇒ 4p = 0
∴ P = o
So (p, 0) = (0, 0) is the point on X-axis, which is equidistant from (5, 7) and (7, 5).

Question 29.
To which quadrants do the following points belong ?
(i) (5, 7)
(ii) (5, – 7)
(iii) (-5, 7)
(iv) (-5, -7)
Solution:
(5, 7) belongs to first quadrant q₁
(5, -7) belongs to fourth quadrant q₄.
(-5, 7) belongs to second quadrant q₂.
(-5, -7) belongs to third quadrant q₃.

Question 30.
What will be the lengths of line seg-ments that are parallel to X-axis, as shown in figure ?

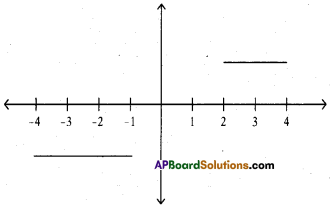
Solution:
In the above figure, length of the line segment above the X-axis is 4 – 2 = 2
And length of line segment below X-axis is 4 – 1 = 3