These AP 10th Class Maths Chapter Wise Important Questions Chapter 6 Progressions will help students prepare well for the exams.
AP State Syllabus 10th Class Maths 6th Lesson Important Questions and Answers Progressions
Question 1.
Check whether – 25 is a term in the progression 5, 3, 1, ………….or not ?
Solution:
The given 5, 3, 1,…………..is an arithmetic
progression here
a = 5, d = a2 – a2 = 3 – 5 = -2
Let -25 is some of ‘n’th term
i.e. an – 25
So an = a + (n-1)d
-25 = 5 + (n – 1)(- 2)
– 25 – 5 = (n – 1) (-2)
\(\frac{-30}{-2}\) = n – 1
⇒ n – 1 = 15 and n = 15+ 1 = 16
So – 25 exist at 16th term in above series.
![]()
Question 2.
Find out the common ratio in the GP 2, 2\(\sqrt{2},\),4…………..
Solution:
The given GP is 2, 2\(\sqrt{2},\), 4, ………………
The common ratio = \(\frac{a_{2}}{a_{1}}=\frac{2 \sqrt{2}}{2}=\sqrt{2}\)
Question 3.
Show that the sum of multiples of 3 bet-ween 1 and 100 is 1683.
Solution:
To show the sum of multiples of 3 bet-ween 1 and 100 is 1683.
The multiples of 3, in between 1 and 100 are 3, 6, 9, 12,… 99 which is an A.P.
In which a = 3, d = 6 – 3 = 3
and number of terms = \(\frac{99}{3}\) = 33.
Now sum of 33 terms of A.P.
3, 6, 9, …. 99 is
Sn = \(\frac{n}{2}\)(a + l)
= \(\frac{33}{2}\) (3 + 99)
= \(\frac{33 \times 102}{2}\)
= 51 × 33
∴ Sum of multiples of ‘3’ = 1683
Question 4.
Find the 8th term of the A.P., 117, 104, 91, 78, ………………
Solution:
In the given A.P., a1 = 117, a2 = 104
Common difference d = a2 – a1
= 104 – 117
= -13
∴ 8th term t8 = a1 + 7d
= 117 + 7(-13)
= 117 – 91 = 26
![]()
Question 5.
Find the common difference of the terms of A.P.
(x – y), (x + y), (x + 3y), ……………
Solution:
Given terms of A.P = (x – y), (x + y), (x + 3y)
then common difference = difference of successive terms
= (x + y) – (x – y) = x + y – x + y = 2y
∴ Common difference of given AP = 2y
Question 6.
\(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}\), ………….. are in G.P. justify.
Solution:
To justify \(\frac{1}{4}, \frac{1}{16}, \frac{1}{64}, \frac{1}{256}\), ………….. is a G.P.
We need to show the ratio of any two successive terms is equal.
Now the common ratio
= r1\(\frac{1}{16} \div \frac{1}{4}=\frac{1}{4}\)
r2 = \(\frac{1}{64} \div \frac{1}{16}=\frac{1}{4}\) ⇒ r1 = r2
Hence it is a G.P.
Question 7.
State Fundamental Theorem of Arith-metic. Model PapeF
Solution:
Statement of Fundamental Theorem of Arithmetic “Every composite number can be expressed as a product of , primes, and this factorization is unique”.
Question 8.
Find the numbe of terms in the follow¬ing A.P.
7,13,19, …………….. ,205
Solution:
Given : 7, 13, 19 …………….., 205 are in A.P
a = 7, d = 6
Let an = 205
a + (n – 1)d = 205 7 + (n – 1)6 = 205 .
(n- 1)6 = 205 -7 (n-1)6 =198 (n – 1) = 33 ⇒ n = 34
Number of terms in the given A.P is 34.
Question 9.
nth term of an A.P. is an . If a1 + a2 + a3 = 102 and a1 = 15, then find a10.
Solution:
Given a1 = 15 and a1 + a2 + a3 =102
a + a + d + a + 2d = 102
⇒ 3a + 3d = 102
⇒ 3 (a + d) = 102
∴ (a + d) = \(\frac{102}{3}\) = 34
⇒ d = 34 – a = 34 – 15 = 19
∴ a = 15, 0 = 19
then its 10th term = a10
= a + (10 – 1)d
= a + 9d = 15 + 9(19)
= 15 + 171 = 186
∴ 10th term of it = 186
Question 10.
How many three digit numbers are divisible by 3 ? Mar. *18|
Solution:
3 Digit numbers which are divisible by
3 are 102, 105, 108, ……………. 999
a = 102, d = 3, nth term = 999
a + (n – 1)d = 999
102 + (n- 1) .3 = 999
(n- 1)3 = 897
n – 1 = \(\frac{897}{3}\) = 299
n = 300
∴ No. of three digit numbers which are divisible by 3 is 300.
Question 11.
If the sum of first 15 terms of an A.P. is 675 and its first term is 10, then find
25th term.
Solution:
In an A,P. first term = a = 10
Sum of first 15 terms
S15 = \(\frac{15}{2}\) (2a + 14d) = 675
⇒ \(\frac{15}{2}\) x 2(10 + 7d) = 675
⇒ 10 + 7d = \(\frac{675}{15}\)
⇒ 10 + 7d = 45
⇒ 7d = 35
∴ d = 5
∴ 25th term = a25 = a + 24d
= 10 + 24 × 5 = 10 + 120 = 130
Question 12.
The first term of a G.P. is 50 and 4th term is 1350. Find the 5th term.
Solution:
Let first term of a GP is ‘a’ and com¬mon ratio is ‘r’.
Given that t1 = a = 50
4th term t4 = ar3 = 1350
⇒ 50r3 = 1350 r3 = \(\frac{1350}{50}\) = 27
∴ r = 3
5th term t5 = ar4
![]()
Question 13.
Check whether -256 is term of G.P -4, -8, -16, ……………
Solution:
The given GP = -4, -8, -16, ……………
∴ a = -4, r = \(\frac{-8}{-4}\) = 2
Let the given -256 is ‘n’th term of given GP.
∴ tn arn-1 = -256
⇒ -4(2)n-1 = -256
⇒ 2n-1 = \(\frac{-256}{-4}\) = 64
2n-1 = 64 = 26
⇒ n -1 = 6
⇒ n = 6 + 1 = 7
-256 is ‘7’th term of given G.P.
Question 14.
A sum of Rs. 1,000 is invested at 8% simple interest per year. Calculate the interest at the end of each year. Do these interests for 1st, 2nd and 3 rd years form an A.P. ? If so, find the total in¬terest to be paid for 30 years making the use of this fact.
Solution:
Sum invested = P = Rs. 1000
Rate of interest = R = 8%
Time of investment = 1 year
∴ Amount of interest (simple)

So the amount of interest for the
years 1, 2, 3, …………….are
80, 160, 240,….. are in an A.P.
In which the first term (a) 5= 80 Common difference (d) = a2 – a1
= 160 – 80 = 80
∴ The amount of interest to be paid in 30 years of time = S30
Sn = j [2a + (n- l)d]
= \(\frac{n}{2}\) [2(80) + (30 – 1) 80]
= 15[160 + 29(80)]
= 15[160 + 2320]
= 2480 × 15 – Rs. 37200
∴ Rs, 37200 will be paid towards interest for 30 years.
Question 15.
If the sum of first 7 terms and 15 terms of an A.P. are 98 and 390 respectively, then find the sum of first 10 terms.
Solution:
Sum of the first 7 terms of AP = 98
\(\frac{7}{2}\)[2a + (7-1)d] = 98
2a + 6d = 98 × \(\frac{2}{7}\)
2a + 6d = 28
a + 3d = 14 ……………..(1)
Sum of the first 15 terms of AP = 390
\(\frac{15}{2}\) [2a + (15 – 1)d] = 390
2a + 14d = 390 × \(\frac{2}{15}\)
2a + 14d – 52
a + 7d = 26 ……………(2)
by solving (1) and (2)
a = 5 and d = 3
Sum of the first 10 terms 10
= \(\frac{10}{2}\) [2a + (10 – 1)d]
– 5[2(5) + 9(3)]
= 5[10 + 27]
= 5 × 37 = 185
Question 16.
Check whether – 321 is a term of the A.P.: 22,15, 8, 1, …………..
Solution:
Given A.P is 22, 15, 8, 1, ……………….
Let an = – 321
a = 22, d = -7
an = a + (n – 1)d
-321 = 22 + (n – 1) (-7)
– 321 = 22 – 7n + 7
– 321 – 29 — – 7n
– 350 – – 7n
n = \(\frac{350}{7}\) = 50
∴ – 321 be a term of given A.P. i.e., 50.
![]()
Question 17.
A man saved ₹ 16,500 in ten years. In each year, after the first, he saved ₹ 100 more than he did in the preceding year. How much aid he save in the first year?
Solution:
Given that S10 = ₹ 16,500; d = ₹ 100; n = 10; a = ?
Sn = \(\frac{n}{2}\) [2a + (n – 1)d]
16,500 = \(\frac{10}{2}\) [2a + (10-1) 100]
16,500 = 5(2a + 900)
\(\frac{16,500}{5}\) = 2a + 900
2a + 900 = 3300
2a = 2400
a = \(\frac{2400}{2}\) = 1200
He saved in the first year = ₹ 1200
Question 18.
An A.P. has 21 terms. The sum of 10th, 11th, 12th terms is 129. The sum of the last 3 terms is 237, then find the A.P.
Solution:
(a + 9d) + (a + 10d) + (a + 11d) = 129
3a + 30d = 129
a + 10d = 43 …………..(1)
(a + 18d) + (a + 19d) + (a + 20d) = 237
3a + 57d = 237
a + 19d = 79 ………………(2)
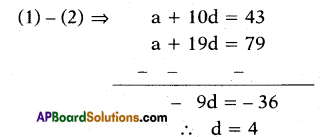
‘d’ value substituting in equation (1)
a + 10(4) = 43
a = 43 – 40 = 3
∴ a = 3
∴ Required A.P. is 3, 7, 11, 15, 19,…
Question 19.
Find the 13th term of the A.P. 2, 7, 12, ……………..
Solution:
In the given A.P. 2, 7, 12, ……………….
The first term (a) = 2
Common difference (d) = a2 – a21
= 7 – 2 = 5
The required term (n) = 13
Formula for nth term in an A.P. is an = a + (n – 1) d ,
Then a13 = 2 + (13 -1)5 = 2 + 12 (5)
= 2 + 60 = 62
So 13th term = 62
Question 20.
In an A.P. the common difference (d) is 6 and seventh term is 36. Can we write such an A.P. ?
Solution:
Yes, we can write the above said A.P.
In the given A.P. (d) = 6
Seventh term a7 = 36
a7 = a + 6d = 36
⇒ a + 6 (6) = 36
∴ a = 36 – 36 = 0
∴ In the given progression a = 0 and d = 6 then it is 0, 6, 12, 18, …………
Question 21.
The ‘n’ th term of a given A.P. is 6n+2. Then write the first four terms in it.
Solution:
In the given A.P. an = 6n + 2
Then the first term = a1
= 6(1) + 2 = 6 + 2 = 8
Second term = a2 = 6 (2) + 2
= 12 + 2 = 14
Third term = a3 = 6 (3) + 2
= 18 + 2 = 20
Fourth term = a4 = 6 (4) + 2
= 24 + 2 = 26
So the first four terms in that A.P. are 8, 14, 20, 26.
Question 22.
In an A.P. the seventh term is 13 and 3rd term is 7. So find ‘a’ and ‘d’ in the method of elimination.
Solution:
In an A.P. the ‘n’th term = an
= a + (n – 1) d
Then a7 = a + (7 – 1) d
= a + 6d = 13 …………..(1)
and a3 = a + (3 – 1) d
= a + 2d = 7 ………….. (2)
Now solving equations (1) & (2) in elimination method
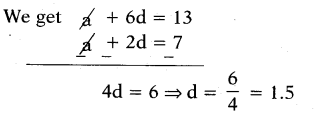
Then a + 2d = 7
a + 2 (1.5) = 7 ⇒ a + 3 = 7
and a = 7 – 3 = 4
So a = 4 and d = 1.5
Question 23.
Which terms are to be known to cal-culate ‘n’ th term of A.P. ?
Solution:
The formula for ‘n’ th term of an A.P. is an = a + (n – 1) d
The variables in. the above formula are a, d, n .
So we should have the above three to calculate an.
Question 24.
Establish the relationship between the first and ‘n’th term of an A.P. in which ‘d’ = 0.
Solution:
Let the first term of that A.P. is ‘a’.
Then common difference (d) = 0 given then nth term = a + (n – 1) d
= a + (n – 1) (0)
= a + 0 = a
∴ an = a
So, when d = 0 is given the ‘n’th term of an A.P. (an) is equal to its first term (a).
![]()
Question 25.
What will be the salary of a person in the year 2020, whose salary in the year 2016 is Rs. 10,000, which in¬creases Rs. 1500 every year ?
Solution:
As the increase (increment) is fixed then it becomes an A.P.
His starting salary in 2016,
= First term of that AP (a)
So (a) = 10,000/-
Increase of salary in every year = Common difference
(d) = Rs. 1500/-
∴ His salary in 2020= 5th term in that A.P.
∴ a5 = a + (n – 1) d
= 10,000 + (5 – 1) (1500)
= 10,000 + 4 (1500)
= 10,000 + 6000 = 16,000/-
His salary in year 2020 is 16000/-
Question 26.
Parking fee for a two wheeler is Rs. 10 per day. i.e., for first day, and then after Rs. 2 for everyday. So what will be the amount to be paid for 15 days ?
Solution:
The additional payment for each day- is fixed. Hence the payments to be made are in G.P. .
Here in this problem
Charges for first day
= First term of AP (a)
∴ a = Rs. 10
Additional charge for each day = Rs. 2
∴ Common difference (d) = 2/-
∴ The A.P. is 10, 12, 14, 16, …………….. (15 terms)
The total amount to be paid for 15 days is S15 = ?
Formula for Sn = \(\) [2a + (n – 1) d]
S15= \(\frac{n}{2}\) [2(10) + (15-1) (2)]
S15= \(\frac{15}{2}\)[20 + 14(2)]
= \(\frac{15}{2}\)[20 + 28]
= \(\frac{15}{2}\) x 48
= 15 × 24 = 360.00
So he has to pay Rs. 360 for 15 days parking.
